
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 6 прямая на плоскости. Плоскость и прямая в пространстве
Лекция 6.1. «Прямая на плоскости. Плоскость и прямая в пространстве» Учебные вопросы: 1. Прямая линия на плоскости 2. Плоскость в пространстве 3. Прямая в пространстве. Взаимное расположение плоскостей и прямых Прямая линии на плоскости Геометрия представляет собой математическую модель, воспроизводящую отношения между объектами, которые могут быть в том или ином смысле отождествлены с точками. В аналитической геометрии точка определяется ее координатами в некоторой системе отсчета и, следовательно, геометрические отношения записываются в виде соотношений между координатами (уравнений, неравенств, систем уравнений или неравенств и др.). Далее, если не оговорено особо, применяется декартова прямоугольная система координат.
Расстояние
координаты середины отрезка
Уравнение вида
связывающее координаты a) b) координаты любой точки, не лежащей на линии Уравнение (1.3.3) в общем случае задает на плоскости некоторое точечное множество, которое может быть и не линией на плоскости. Плоскую линию можно задать также двумя уравнениями
где Значения координат
определяют точку пересечения этих кривых. Число точек пересечения равно числу решений этой системы. Если система не имеет решений, то линии не пересекаются. В зависимости от исходных данных и решаемой задачи уравнение прямой линии на плоскости может иметь различный вид. Каноническое (симметричное) уравнение прямой. Прямую можно задать точкой
Уравнение (1.3.5) называется каноническим (симметричным) уравнением прямой. Направление прямой может быть задано вектором
Уравнение (1.3.6) можно записать в виде
 и и  и определяет при и определяет при  и и  одновременно не равных нулю прямую линию на плоскости. Обратно, каждая прямая линия на плоскости может быть определена линейным уравнением (1.3.7). При одновременно не равных нулю прямую линию на плоскости. Обратно, каждая прямая линия на плоскости может быть определена линейным уравнением (1.3.7). При  прямая проходит через начало координат. При прямая проходит через начало координат. При  прямая проходит параллельно оси прямая проходит параллельно оси 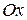 , при , при 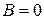 – параллельно оси – параллельно оси  . Для примера на рис. 1.21 приведены прямые, соответствующие уравнениям . Для примера на рис. 1.21 приведены прямые, соответствующие уравнениям  , ,  , ,  . .
Коэффициенты в общем уравнении прямой (1.3.7) определяют координаты нормального и направляющего векторов этой прямой:
Пример. Дана прямая ◄ а) Направляющий вектор б) В качестве направляющего вектора прямой
Общее уравнение прямой (1.3.7) можно переписать в виде
Уравнение прямой можно также записать в виде
Это уравнение называется уравнением прямой в отрезках и определяет прямую линию, пересекающую ось
Условием, при котором три точки плоскости
◄ Используя (1.3.10), получаем уравнение искомой прямой:
Обозначив в каноническом уравнении (1.3.5) отношение через
Угол между прямыми можно найти также при помощи их нормальных векторов
Если прямые заданы уравнениями с угловым коэффициентом
Из этой формулы следует, что прямые параллельны при Пример. Найти угол между прямыми ◄ Используем формулу (1.3.13). По уравнениям прямых находим их нормальные векторы: Используем также формулу (1.3.14). Преобразовав уравнения прямых в форму с угловым коэффициентом: Получен целый набор значений угла
Плоскость в пространстве
проведенным из начала координат в эту точку. Расстояние
координаты середины отрезка
Уравнение вида
a)
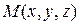 поверхности поверхности  удовлетворяют этому уравнению (рис. 1.36); удовлетворяют этому уравнению (рис. 1.36);
b) координаты любой точки, не лежащей на поверхности Уравнение (1.3.26) в общем случае задает в пространстве некоторое точечное множество, которое может быть и не поверхностью в пространстве. Пример. Уравнение
Значения координат
определяют линию пересечения этих поверхностей. Если система не имеет решений, то поверхности не пересекаются. Уравнение плоскости можно получить следующим образом. Пусть
Полученное уравнение есть уравнение плоскости, проходящей через заданную точку Уравнение (1.3.27) можно переписать в виде
где
Пример. Составить уравнение плоскости, проходящей через точку ◄ Так как искомая плоскость Особые случаи положения плоскости относительно системы координат, задаваемых общим уравнением (1.3.28): 1) 2)
3) 4) Уравнение плоскости в зависимости от решаемой задачи может быть задано в различных формах. Плоскость, пересекающая ось
Уравнение плоскости, проходящей через три данные точки
Пример. Составить уравнение плоскости, проходящей через точки ◄ Подставляя координаты данных точек в формулу (1.3.31), будем иметь
|
||||||||||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 553; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.221.98.71 (0.062 с.) |

 На плоскости каждая ее точка
На плоскости каждая ее точка  (рис. 1.17) представляется двумя координатами: абсциссой
(рис. 1.17) представляется двумя координатами: абсциссой  и ординатой
и ординатой  (записывается
(записывается  ).
). между точками плоскости
между точками плоскости 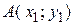 и
и 
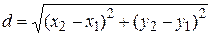 ; (1.3.1)
; (1.3.1) (точки
(точки  ) (рис.1.18):
) (рис.1.18):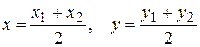 . (1.3.2)
. (1.3.2)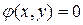 или
или  , (1.3.3)
, (1.3.3) , если:
, если: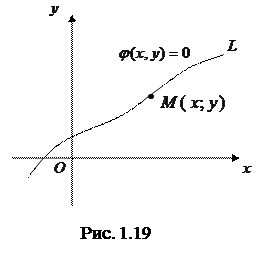 координаты каждой точки
координаты каждой точки  линии
линии  , (1.3.4)
, (1.3.4) – переменный параметр (параметрическое задание линии).
– переменный параметр (параметрическое задание линии).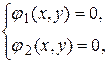
 , лежащего на прямой или параллельного ей (рис. 1.20). Этот вектор называется направляющим вектором прямой. Вектор
, лежащего на прямой или параллельного ей (рис. 1.20). Этот вектор называется направляющим вектором прямой. Вектор  , проведенный из точки
, проведенный из точки  , лежит на прямой и параллелен (коллинеарен) направляющему вектору. Условием коллинеарности векторов является пропорциональность их соответствующих координат, т. е.
, лежит на прямой и параллелен (коллинеарен) направляющему вектору. Условием коллинеарности векторов является пропорциональность их соответствующих координат, т. е. . (1.3.5)
. (1.3.5) , которому она перпендикулярна (рис. 1.20). Этот вектор называют нормальным вектором прямой. Условием перпендикулярности векторов
, которому она перпендикулярна (рис. 1.20). Этот вектор называют нормальным вектором прямой. Условием перпендикулярности векторов  . (1.3.6)
. (1.3.6) Уравнение (1.3.6) есть уравнение прямой, проходящей через данную точку плоскости перпендикулярно данному вектору.
Уравнение (1.3.6) есть уравнение прямой, проходящей через данную точку плоскости перпендикулярно данному вектору. . (1.3.7)
. (1.3.7) . Следует отметить, что эти векторы определяются с точностью до постоянного множителя, т. е. векторы
. Следует отметить, что эти векторы определяются с точностью до постоянного множителя, т. е. векторы  и
и  , где
, где  – любое не равное нулю число, также могут быть взяты в качестве нормального и направляющего вектора соответственно.
– любое не равное нулю число, также могут быть взяты в качестве нормального и направляющего вектора соответственно. (
( ). Составить уравнения прямых, проходящих через точку
). Составить уравнения прямых, проходящих через точку  а) параллельно данной прямой (
а) параллельно данной прямой (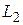 ), б) перпендикулярно данной прямой (
), б) перпендикулярно данной прямой ( ).
).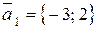 для данной прямой
для данной прямой 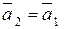 ). Каноническое уравнение прямой
). Каноническое уравнение прямой  . Отсюда получаем общее уравнение прямой
. Отсюда получаем общее уравнение прямой  . Это же уравнение можно получить другим путем. Записав общее уравнение прямой
. Это же уравнение можно получить другим путем. Записав общее уравнение прямой  (коэффициенты
(коэффициенты 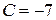 .
. . Каноническое уравнение прямой
. Каноническое уравнение прямой  . Отсюда
. Отсюда  . ►
. ► или (положив
или (положив  ,
,  )
) ,
,  (1.3.8)
(1.3.8) Уравнение (1.3.8) называется уравнением прямой с угловым коэффициентом. Оно определяет прямую, образующую угол
Уравнение (1.3.8) называется уравнением прямой с угловым коэффициентом. Оно определяет прямую, образующую угол  с положительным направлением оси
с положительным направлением оси  . Коэффициент
. Коэффициент 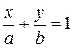 . (1.3.9)
. (1.3.9) и ось
и ось 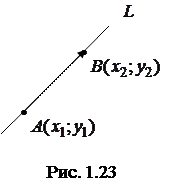 Уравнение прямой, проходящей через две данные (несовпадающие) точки
Уравнение прямой, проходящей через две данные (несовпадающие) точки  и
и  , следует из канонического уравнения (1.3.5), если в качестве направляющего вектора прямой
, следует из канонического уравнения (1.3.5), если в качестве направляющего вектора прямой  взять вектор
взять вектор 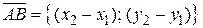 и выбрать точку
и выбрать точку  или
или  . (1.3.10)
. (1.3.10) лежат на одной прямой, является
лежат на одной прямой, является .
. Пример. Составить уравнение прямой, проходящей через точки
Пример. Составить уравнение прямой, проходящей через точки  и
и  . Записать это уравнение в виде уравнения в отрезках и построить прямую.
. Записать это уравнение в виде уравнения в отрезках и построить прямую.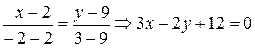 . Переписываем уравнение в форму уравнения в отрезках:
. Переписываем уравнение в форму уравнения в отрезках:  . Из последнего уравнения имеем
. Из последнего уравнения имеем  ,
,  . Прямая приведена на рис. 1.24. ►
. Прямая приведена на рис. 1.24. ► (1.3.11)
(1.3.11) Под углом
Под углом  между двумя пересекающимися прямыми
между двумя пересекающимися прямыми  ) равен углу между направляющими векторами
) равен углу между направляющими векторами  и
и 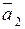 прямых (рис. 1.25), т.е. (с точностью до знака)
прямых (рис. 1.25), т.е. (с точностью до знака) . (1.3.12)
. (1.3.12) и
и  :
: . (1.3.13)
. (1.3.13) ,
,  , то угол между ними можно определить по формуле
, то угол между ними можно определить по формуле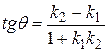 . (1.3.14)
. (1.3.14) и перпендикулярны при
и перпендикулярны при  (
( ).
). и
и 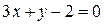 .
. ,
,  . Согласно (1.3.13) будем иметь
. Согласно (1.3.13) будем иметь  . Отсюда
. Отсюда  ,
,  (смежные углы).
(смежные углы). ,
,  , получаем угловые коэффициенты
, получаем угловые коэффициенты  ,
,  . Подставив значения коэффициентов в (1.3.14), получаем
. Подставив значения коэффициентов в (1.3.14), получаем  . Отсюда
. Отсюда  или
или  .
. В пространстве каждая его точка
В пространстве каждая его точка  (записывается
(записывается  ). Точка также может быть задана своим радиус-вектором
). Точка также может быть задана своим радиус-вектором ,
,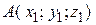 и
и 
 ;
; ,
, 
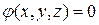 или
или  (1.3.26)
(1.3.26) связывающее координаты
связывающее координаты  точек пространства, называется уравнением поверхности
точек пространства, называется уравнением поверхности 
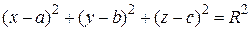 есть уравнение радиуса
есть уравнение радиуса  с центром в точке с координатами
с центром в точке с координатами  ; уравнение
; уравнение  не задает ни одной точки в пространстве (его решением является пустое множество).
не задает ни одной точки в пространстве (его решением является пустое множество).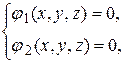
 – любой вектор, перпендикулярный данной плоскости
– любой вектор, перпендикулярный данной плоскости  (нормальный вектор плоскости), а
(нормальный вектор плоскости), а  – точка, через которую плоскость проходит (рис. 1.37). Любой вектор
– точка, через которую плоскость проходит (рис. 1.37). Любой вектор  , проведенный из точки
, проведенный из точки  в произвольную точку плоскости
в произвольную точку плоскости  , будет перпендикулярен вектору
, будет перпендикулярен вектору  и, следовательно, их скалярное произведение
и, следовательно, их скалярное произведение  , т. е.
, т. е.
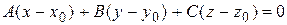 .(1.3.27)
.(1.3.27) или
или  (1.3.28)
(1.3.28) . Это уравнение также линейно относительно координат и называется общим уравнением плоскости: при
. Это уравнение также линейно относительно координат и называется общим уравнением плоскости: при  не равных нулю одновременно оно определяет плоскость с нормальным вектором
не равных нулю одновременно оно определяет плоскость с нормальным вектором 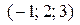 параллельно плоскости
параллельно плоскости  .
.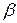 параллельна плоскости
параллельна плоскости 

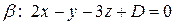 . Величину
. Величину  найдем из условия, что искомая плоскость проходит через точку
найдем из условия, что искомая плоскость проходит через точку  . Окончательно, искомое уравнение плоскости
. Окончательно, искомое уравнение плоскости  . ►
. ► плоскость
плоскость  , проходящая через начало координат;
, проходящая через начало координат;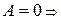 плоскость
плоскость  параллельна оси
параллельна оси  при
при 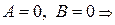 плоскость
плоскость  параллельна координатной плоскости
параллельна координатной плоскости 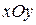 (
( при
при  ,
, 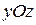 при
при  );
);
 – уравнение координатной плоскости
– уравнение координатной плоскости  –
–  –
–  , ось
, ось 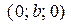 и ось
и ось  (рис. 1.38) имеет уравнение (уравнение плоскости в отрезках)
(рис. 1.38) имеет уравнение (уравнение плоскости в отрезках)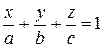 . (1.3.29)
. (1.3.29) Пусть
Пусть  – расстояние плоскости от начала координат (длина перпендикуляра
– расстояние плоскости от начала координат (длина перпендикуляра 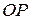 , опущенного из начала координат на плоскость) (рис. 1.39),
, опущенного из начала координат на плоскость) (рис. 1.39), 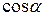 ,
,  ,
,  – направляющие косинусы нормального вектора
– направляющие косинусы нормального вектора 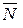 :
:  , длина
, длина 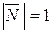 , т. к.
, т. к.  . Тогда уравнение плоскости имеет вид (нормальное уравнение плоскости)
. Тогда уравнение плоскости имеет вид (нормальное уравнение плоскости)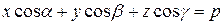 . (1.3.30)
. (1.3.30) ,
,  ,
,  , не лежащие на одной прямой, имеет вид
, не лежащие на одной прямой, имеет вид . (1.3.31)
. (1.3.31) ,
,  и
и 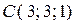 .
.


 . Так как в полученном уравнении плоскости нет слагаемого с координатой
. Так как в полученном уравнении плоскости нет слагаемого с координатой 


