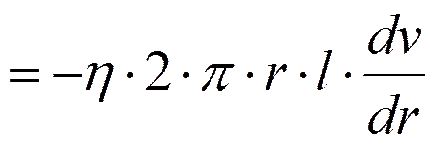Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Классическая статистика. Функция распределения Максвелла. Барометрическая формула. Распределение Больцмана. ⇐ ПредыдущаяСтр 3 из 3
Классическая статистика. Функция распределения Максвелла. Барометрическая формула. Распределение Больцмана. Закон равномерного распределения энергии по степеням свободы молекул.
В классической статистической физике выводится закон Больцмана о равномерном распределении энергии по степеням свободы молекул: для статистической системы, находящейся в состоянии термодинамического равновесия, на каждую поступательную и вращательную степени свободы приходится в среднем кинетическая энергия, равная kT/ 2, а на каждую колебательную степень свободы — в среднем энергия, равная kT. Колебательная степень «обладает» вдвое большей энергией потому, что на нее приходится не только кинетическая энергия (как в случае поступательного и вращательного движений), но и потенциальная, причем средние значения кинетической и потенциальной энергий одинаковы. Таким образом, средняя энергия молекулы
где i — сумма числа поступательных, числа вращательных в удвоенного числа колебательных степеней свободы молекулы:
Внутренняя энергия для произвольной массы т газа.
где М — молярная масса.
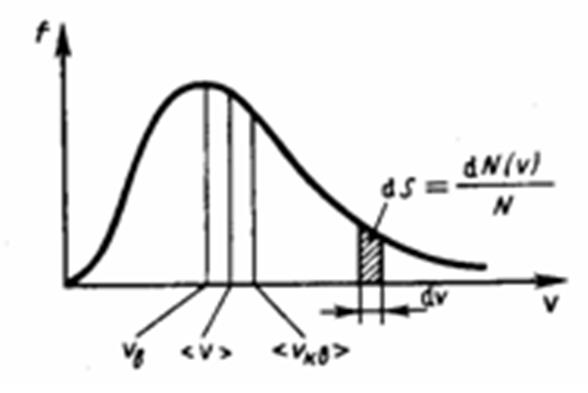
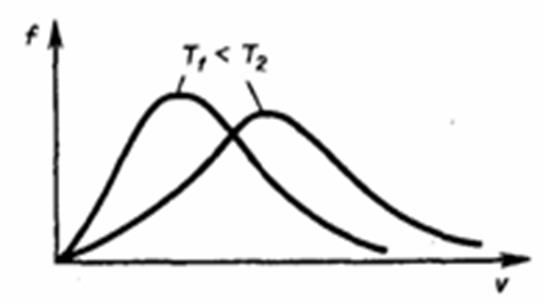
Классическое распределение по скоростям (распределение Максвелла):
dN – число частиц, попадающих в определенный интервал скоростей. N – число всех частиц. f(V) – функция распределения по скоростям dV – элементарный объем скоростей.
Рассмотрим функцию распределения по скоростям в сферической системе координат:
Величина А (амплитуда вероятности) находится из условия нормировки:
Аналогично находим j(vy) и j(vz):
тогда
Первое закон термодинамики.
Внутренняя энергия системы. Теплоемкость вещества. Первый закон термодинамики. Применение первого закона термодинамики к изопроцессам в идеальном газе. Адиабатический процесс.
Внутренняя энергия газа
Применение первого начала термодинамики к изопроцессам.
Изохорный процесс (V =const).
Изобарный процесс (p =const).
Изотермический процесс (T =const).
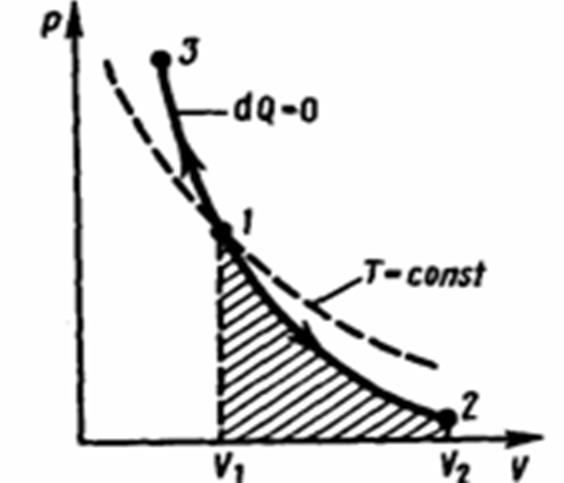
Адиабатический процесс.
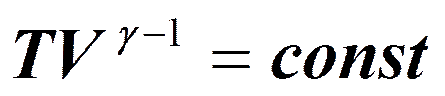
Уравнения Пуассона:
12. Второе начало термодинамики Краткая формулировка второго начала термодинамики:
в процессах, происходящих в замкнутой системе, энтропия не убывает. две формулировки второго начала термодинамики: 1) по Кельвину: невозможен круговой процесс, единственным результатом которого является превращение теплоты, полученной от нагревателя, в эквивалентную ей работу; 2) по Клаузиусу: невозможен круговой процесс, единственным результатом которого является передача теплоты от менее нагретого тела к более нагретому. Первое начало термодинамики, выражая закон сохранения и превращения энергии, не позволяет установить направление протекания термодинамических процессов.
Первые два начала термодинамики дают недостаточно сведений о поведении термодинамических систем при нуле Кельвина. Они дополняются третьим началом термодинамики, или теоремой Нернста — Планка: энтропия всех тел в состоянии равновесия стремится к нулю по мере приближения температуры к нулю Кельвина:
Явления переноса. Законы диффузии, теплопроводности и внутреннего трения (вязкости) и их обоснование в молекулярно-кинетической теории. Движение жидкости (газа) по трубам. Формула Пуазейля.
Выведем основное уравнение явления переноса:
j - переносимый параметр Dx = 2<l>
<l> – средняя длина свободного пробега молекул.
1) Диффузия j = m;
2) Теплопроводность
3.Внутреннее трение j = p = mV
Рейнольдс установил, что характер течения зависит от безразмерной величины, называемой числом Рейнольдса: r — плотность жидкости; (v)—средняя по сечению трубы скорость жидкости; d — характерный линейный размер, например диаметр трубы. При малых значениях числа Рейнольдса (Re£1000) наблюдается ламинарное течение, переход от ламинарного течения к турбулентному происходит в области 1000£:Re£2000, а при Re = 2300 (для гладких труб) течение — турбулентное. Если число Рейнольдса одинаково, то режим течения различных жидкостей (газов) в трубах разных сечений одинаков. Методы определения вязкости 1. Метод Стокса. Этот метод определения вязкости основан на измерении скорости медленно движущихся в жидкости небольших тел сферической формы.
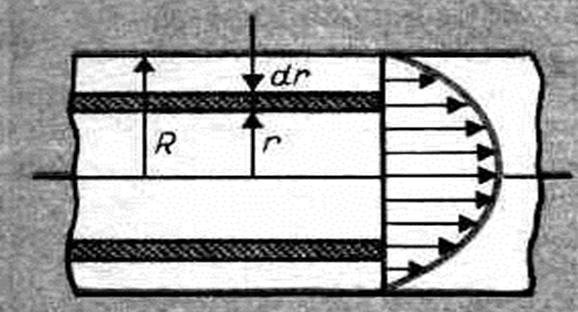
2. Метод Пуазейля. Этот метод основан на ламинарном течении жидкости в тонком капилляре. Рассмотрим капилляр радиусом R и длиной l. В жидкости мысленно выделим цилиндрический слой радиусом r и толщиной dr (рис. 54).
Сила внутреннего трения, действующая на боковую поверхность этого слоя,
где dS — боковая поверхность цилиндрического слоя; знак минус означает, что при возрастании радиуса скорость уменьшается. Для установившегося течения жидкости сила внутреннего трения, действующая на боковую поверхность цилиндра, уравновешивается силой давления, действующей на его основание:
После интегрирования, полагая, что у стенок имеет место прилипание жидкости, т. е. скорость на расстоянии R от оси равна нулю, получим
Отсюда видно, что скорости частиц жидкости распределяются по параболическому закону, причем вершина параболы лежит на оси трубы.
откуда вязкость
14.
Поверхностное натяжение Поверхностное натяжение равно силе поверхностного натяжения, приходящейся на единицу длины контура, ограничивающего поверхность. Единица поверхностного натяжения — ньютон на метр (Н/м) или джоуль на квадратный метр (Дж/м2) Большинство жидкостей при температуре 300 К имеет поверхностное натяжение порядка 10-2—10-1 Н/м. Поверхностное натяжение с повышением температуры уменьшается, так как увеличиваются средние расстояния между молекулами жидкости.
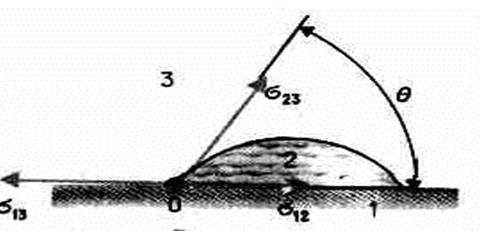
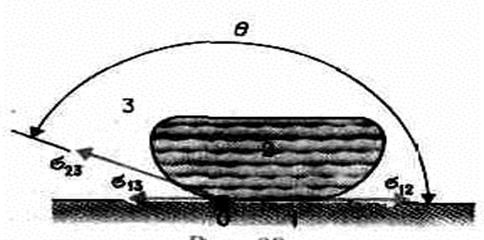
Из практики известно, что капля воды растекается на стекле и принимает форму, изображенную на рис. 98, в то время как ртуть на той же поверхности превращается в несколько сплюснутую каплю (рис. 99). В первом случае говорят, что жидкость смачивает твердую поверхность, во втором — не смачивает ее. Смачивание зависит от характера сил, действующих между молекулами поверхностных слоев соприкасающихся сред.
Полное смачивание (в данном случае q=0). Если s12>s13+s23, то жидкость стягивается в шаровую каплю, в пределе имея с ней лишь одну точку соприкосновения (например, капля воды на поверхности парафина),— имеет место полное несмачивание (в данном случае q=p). . Теплоемкость твердых тел В качестве модели твердого тела рассмотрим правильно построенную кристаллическую решетку, в узлах которой частицы (атомы, ионы, молекулы), принимаемые за материальные точки, колеблются около своих положений равновесия — узлов решетки — в трех взаимно перпендикулярных направлениях. Таким образом, каждой составляющей кристаллическую решетку частице приписывается три колебательных степени свободы, каждая из которых, согласно закону равнораспределения энергии по степеням свободы (см. § 50), обладает энергией kT. Внутренняя энергия моля твердого тела Um = 3NАkT = 3RT, где NА — постоянная Авогадро; N A k=R (R — молярная газовая постоянная). Молярная теплоемкость твердого тела
т. е. молярная (атомная) теплоемкость химически простых тел в кристаллическом состоянии одинакова (равна 3R) и не зависит от температуры. Этот закон был эмпирически получен французскими учеными П. Дюлонгом (1785—1838) и Л. Пти (1791 —1820) и носит название закона Дюлонга и Пти. Если твердое тело является химическим соединением (например, NaCl), то число частиц в моле не равно постоянной Авогадро, а равно nN A, где n — число атомов в молекуле (для NaCl число частиц в моле равно 2 N а, так, в одном моле NaCl содержится NA атомов Na и NA атомов Cl). Таким образом, молярная теплоемкость твердых химических соединений CV = 3pR»25n Дж/(моль•К),
т. е. равна сумме атомных теплоемкостей элементов, составляющих это соединение.
Рассматривая непрерывный спектр частот осцилляторов, П. Дебай показал, что основной вклад в среднюю энергию квантового осциллятора вносят колебания низких частот, соответствующих упругим волнам. Поэтому тепловое возбуждение твердого тела можно описать в виде упругих волн, распространяющихся в кристалле. По Дебаю:
Классическая статистика. Функция распределения Максвелла. Барометрическая формула. Распределение Больцмана. Закон равномерного распределения энергии по степеням свободы молекул.
В классической статистической физике выводится закон Больцмана о равномерном распределении энергии по степеням свободы молекул: для статистической системы, находящейся в состоянии термодинамического равновесия, на каждую поступательную и вращательную степени свободы приходится в среднем кинетическая энергия, равная kT/ 2, а на каждую колебательную степень свободы — в среднем энергия, равная kT. Колебательная степень «обладает» вдвое большей энергией потому, что на нее приходится не только кинетическая энергия (как в случае поступательного и вращательного движений), но и потенциальная, причем средние значения кинетической и потенциальной энергий одинаковы. Таким образом, средняя энергия молекулы
где i — сумма числа поступательных, числа вращательных в удвоенного числа колебательных степеней свободы молекулы:
Внутренняя энергия для произвольной массы т газа.
где М — молярная масса.
Классическое распределение по скоростям (распределение Максвелла):
dN – число частиц, попадающих в определенный интервал скоростей. N – число всех частиц. f(V) – функция распределения по скоростям dV – элементарный объем скоростей.
Рассмотрим функцию распределения по скоростям в сферической системе координат:
Величина А (амплитуда вероятности) находится из условия нормировки:
Аналогично находим j(vy) и j(vz):
тогда
Первое закон термодинамики.
Внутренняя энергия системы. Теплоемкость вещества. Первый закон термодинамики. Применение первого закона термодинамики к изопроцессам в идеальном газе. Адиабатический процесс.
Внутренняя энергия газа
|
|||||||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 1425; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.143.4.181 (0.182 с.) |
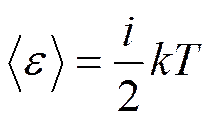
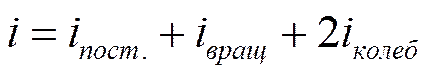
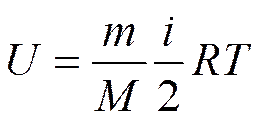
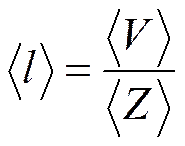
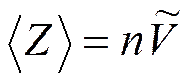
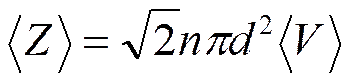
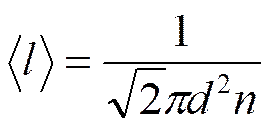
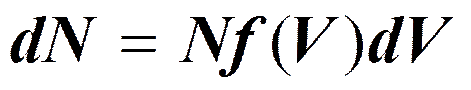

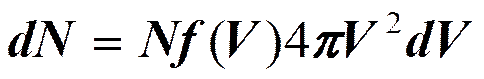
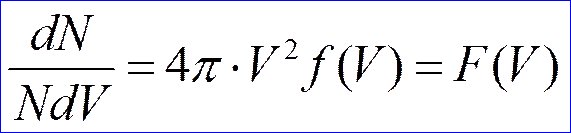 - функция распределения Максвелла.
- функция распределения Максвелла.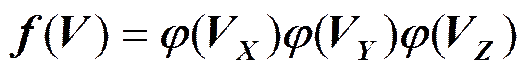

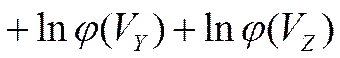
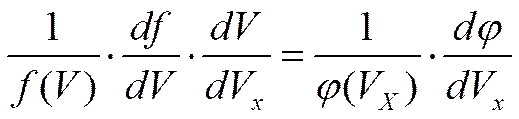
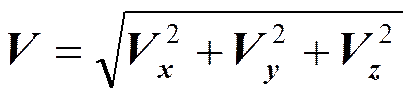
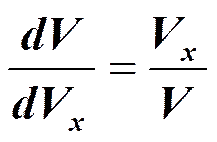
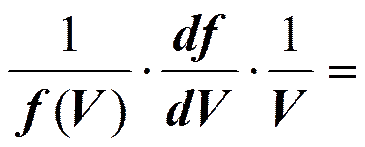
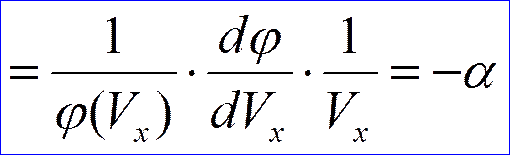
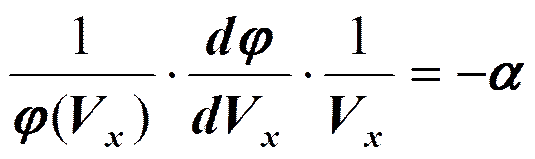
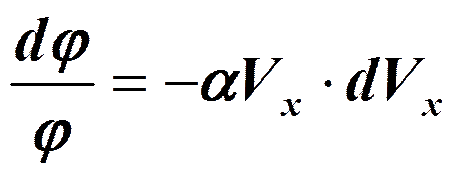
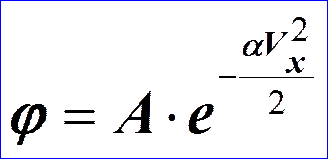
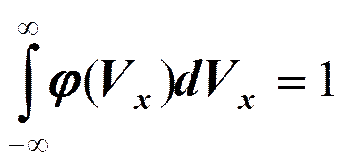 - условие нормировки
- условие нормировки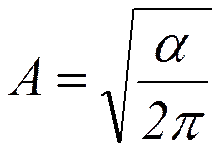 ;
; 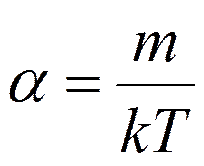
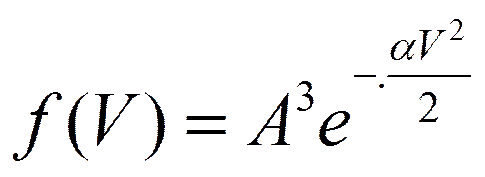

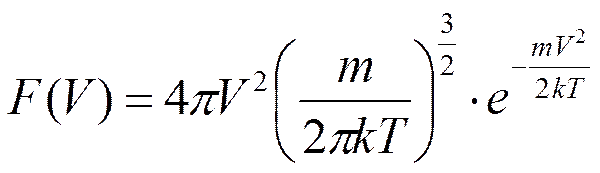
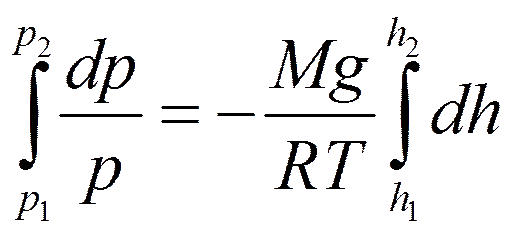
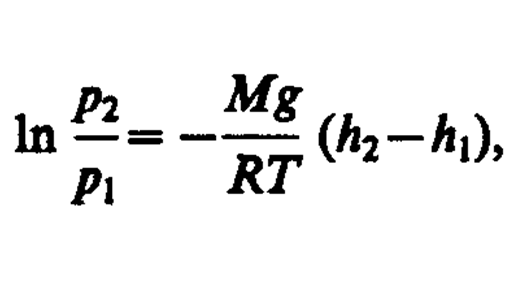
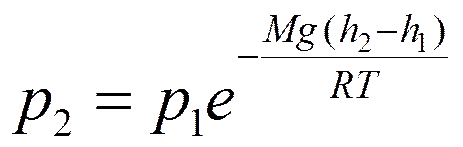
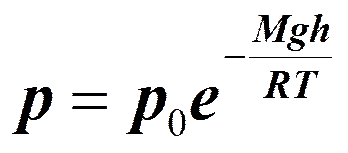
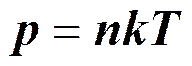
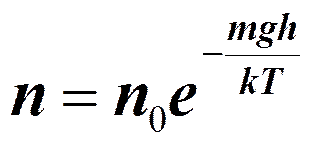
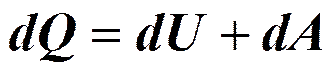
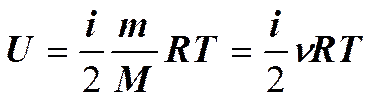
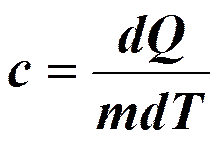
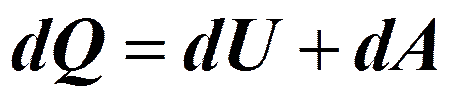

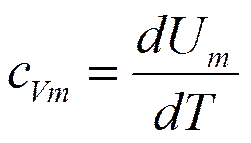
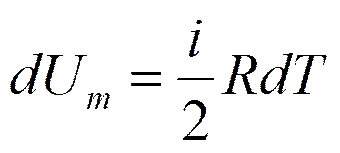

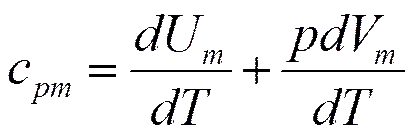
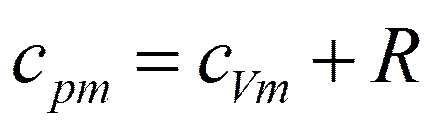
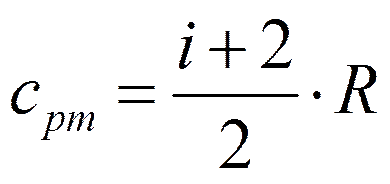
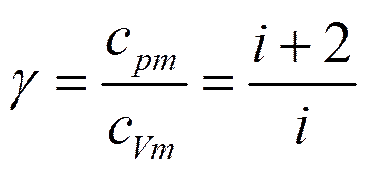
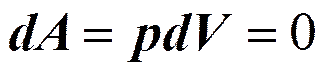
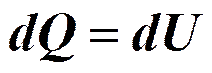
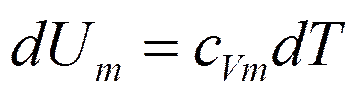
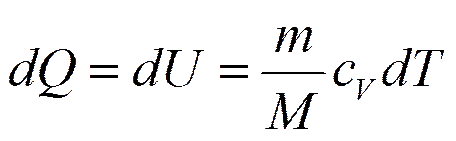
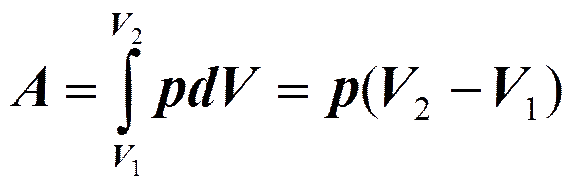
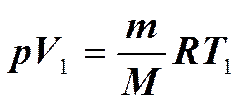
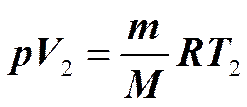
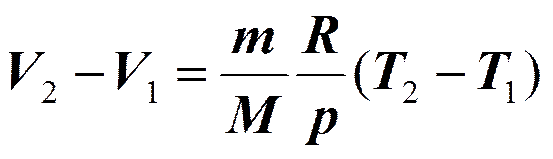
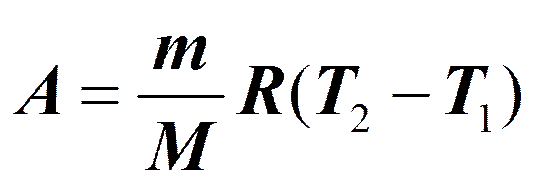
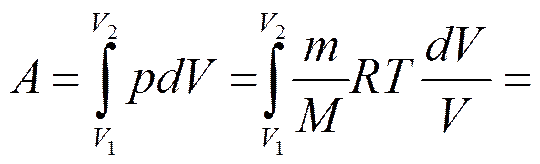
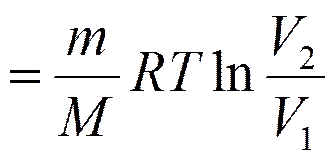
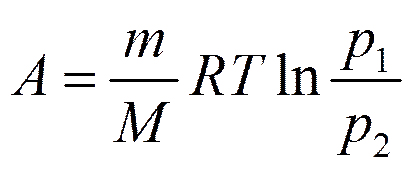
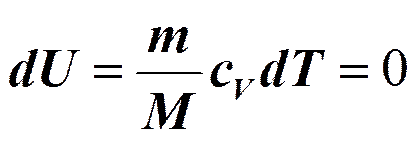
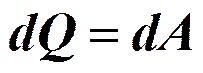
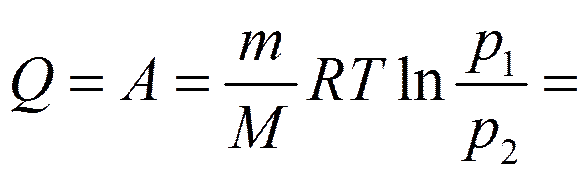
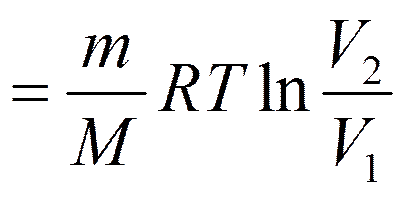
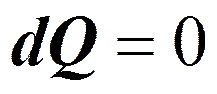
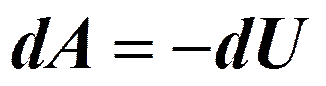
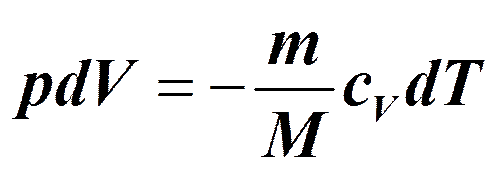
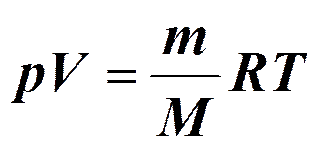
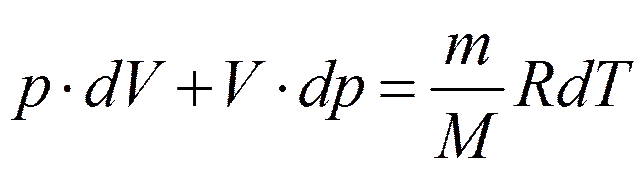
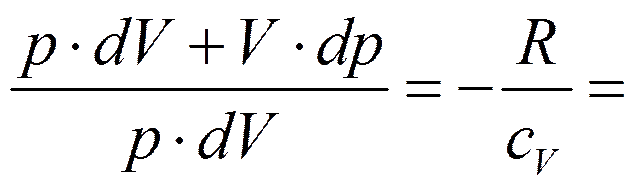
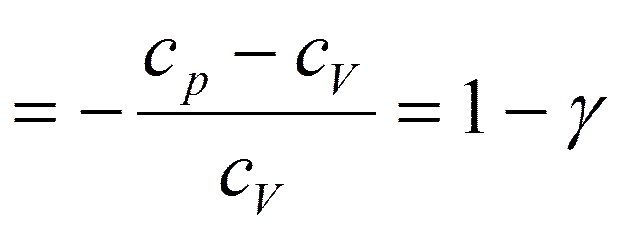
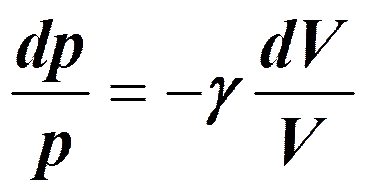
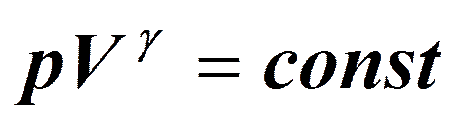
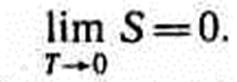



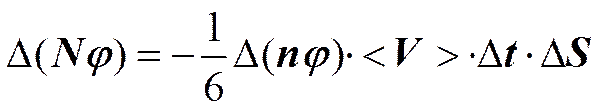

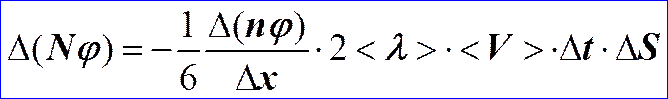 - основное уравнение явления переноса.
- основное уравнение явления переноса.
 - уравнение диффузии (уравнение Фика).
- уравнение диффузии (уравнение Фика). - градиент плотности.
- градиент плотности.

 ; (i – степень свободы, i = 3, 5,6)
; (i – степень свободы, i = 3, 5,6)






 - уравнение теплопроводности (уравнение Фурье).
- уравнение теплопроводности (уравнение Фурье). -
-

 =
= - уравнение трения (уравнение Ньютона).
- уравнение трения (уравнение Ньютона).

 — кинематическая вязкость;
— кинематическая вязкость;