
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теорема 3. Проекция суммы двух векторов на ось равна сумме слагаемых векторов на ту же ось
Координатами
Эта формула называется разложением вектора по ортам Модуль вектора равен квадратному корню из суммы квадратов его проекций на оси координат
Направляющими косинусами вектора
Действия над векторами, заданными Своими координатами Пусть даны векторы
или При умножении вектора на число все его координаты умножаются на это число
Два вектора aх = bx; ay = by; az = bz .
Необходимым и достаточным условием коллинеарности векторов
Если известны координаты начала А(х1, у1, z1) и конца В(х2, у2, z2) вектора Длину вектора, заданного координатами начала и конца, вычисляют по формуле
Пример. Даны векторы
= (2 - 9; -6 -12; 4 -(-15)) = (-7; -18; 19);
= (3; -9; 6) + (12; 16; -20)=(3 + 12; -9 + 16; 6 + (-20)) = (15; 7; -14). Пример. Даны две точки А(9; -7; -4) и В(-1; 3; 1). Найти координаты и длину вектора
Пример. Дан вектор Разложение вектора Длина вектора Орт вектора Пример. Определить, при каких a и b векторы Запишем условие коллинеарности векторов: Пример. Найти длину и направляющие косинусы вектора Найдем координаты вектора Модуль вектора
Скалярное произведение векторов, Его свойства Скалярным произведением двух векторов называется число, равное произведению длин векторов на косинус угла между ними. Обозначается
Свойства скалярного произведения: 1) 2) 3)
4) скалярное произведение равно нулю тогда и только тогда, когда векторы 5) скалярный квадрат вектора равен квадрату его длины: Пусть даны два вектора Скалярное произведение двух векторов равно сумме произведений их одноименных координат
Условие перпендикулярности двух ненулевых векторов
Косинус угла между двумя векторами определяется по формуле:
Проекция вектора
Пример. Найти длину вектора По свойству 5:
= = 81 + 72 + 64 = 217, Пример. Найти косинус угла между векторами
= Пример. При каком значении l векторы Условие перпендикулярности записывается: Пример. Даны векторы Имеем
Примеры для самостоятельной работы 1. Найти длины диагоналей параллелограмма, построенного на векторах 2. Найти угол между единичными векторами 3. Даны вершины треугольника А(4; 1; 0); В(2; 2; 1) и С(6; 3; 1). Найти проекцию стороны АВ на АС, угол между сторонами АВ и АС. 4. При каком a векторы 5. Известно, что 6. Даны векторы ПРЯМАЯ ЛИНИЯ НА ПЛОСКОСТИ
Если известны точка М0(х0, у0) на прямой l и направляющий вектор
Если известны точка М0(х0, у0) на прямой l и вектор А(х -х0) + В(у -у0) = 0. Вектор Ах + Ву + С = 0. Если С = 0, то прямая проходит через начало координат, ее уравнение Ах + Ву = 0. Если А = 0, то прямая параллельна оси Ох, ее уравнение Если В = 0, то прямая параллельна оси Оу и
Если А = С = 0, то у = 0 – ось Ох. Если В = С = 0, то х = 0 – ось Оу. Пусть даны уравнения двух прямых 1) совпадают, если 2) параллельны, если 3) перпендикулярны, если A1А2 + B1В2 = 0. Для нахождения точки пересечения прямых решают систему уравнений
Уравнение вида у = kx + b называется уравнением прямой с угловым коэффициентом, где k = tga - тангенс угла наклона прямой, b – координата точки пересечения прямой с осью Oу. Если даны уравнения двух прямых у = k1x + b1; у = k2x + b2, то а) угол между прямыми определяется по формуле
б) если k1 = k2, то прямые параллельны; в) если Уравнение прямой, проходящей через данную точку М0(х0, у0) с угловым коэффициентом k имеет вид:
Уравнение прямой, проходящей через две данные точки М1(х1, у1) и М2(х2, у2):
Расстояние от точки М0(х0, у0) до прямой Ах + Ву + С = 0 вычисляется по формуле
Пусть даны точки А(х1, у1) и В(х2, у2). Координаты точки М, делящей отрезок АВ в заданном отношении
Пример. Даны точка М(3; 4) на прямой l и направляющий вектор Уравнение имеет вид Пример. Даны точки М1(4; -2) и М2 (3; 1). Написать уравнение прямой, проходящей через точки М1 и М2. Уравнение прямой записывается Пример. Написать уравнение прямой, проходящей через точку А (1; -2) параллельно прямой 3х + 4у – 5 = 0. Найдем угловой коэффициент данной прямой, выразим
Искомая прямая имеет уравнение Подставим координаты точки А в это уравнение:
Пример. Определить взаимное расположение прямых х + 2у -3 = 0 и 5х + 10у - 2 = 0. Имеем Пример. Найти расстояние от точки М(-1; 1) до прямой 4х - 3у + 6 = 0. Искомое расстояние находится по формуле
Примеры для самостоятельной работы 1. Найти проекцию точки А(-1; 2) на прямую 3х - 5у - 21 = 0. 2. Даны вершины параллелограмма А(9; -3), В(4; -2) и С(-7; -5). Найти уравнения диагоналей. 3. Дан треугольник с вершинами А(5; -4), В(-1; 3) и С(-3; -2). Найти: а) уравнение высоты ВD; б) уравнение меридианы ВМ; в) угол между высотой и медианой ВМ. 4. Доказать, что три точки А(3; -5), В(-1; 1) и С(-3; 4) лежат на одной прямой. 5. Стороны треугольника заданы уравнениями: 7х - 6у + 9 = 0; 5х + 2у - 25 = 0; 3х + 10у + 29 = 0. Найти координаты вершин и уравнения высот треугольника. КРИВЫЕ ВТОРОГО ПОРЯДКА Кривой второго порядка называется линия, определяемая уравнением второй степени относительно текущих декартовых координат. В общем виде уравнение имеет вид: Ах2 + 2Вху + Су2 + 2Dx + 2Еу + F = 0. 1. Окружность – множество точек плоскости, равноудаленных от данной. Каноническое уравнение окружности (х - х0)2 + (у - у0)2 = R2, где точка С(х0, у0) – центр окружности, R – ее радиус. Пример. Определить вид кривой х2 + у2 - 6х + 4у – 12 = 0. Выделим полный квадрат для каждой переменной х и у: х2 - 6х + 9 – 9 + у2 + 4у + 4 – 4 – 12 = 0, (х - 3)2 + (у + 2)2 = 25 – это уравнение окружности с центром в точке С(3; -2) и R = 5. 2. Эллипсом называется множество всех точек плоскости, сумма расстояний которых до двух данных точек F1 и F2, называемых фокусами, есть величина постоянная (2а). F1M + F2M = 2a. Каноническое уравнение эллипса имеет вид: (b2 = a2 - c2, a > c), F1(-с; 0) и F2 (с; 0) – фокусы.
Точки А1 (-а, 0), А2 (а, 0), В1 (0, -b), В2 (0, b) называются вершинами эллипса, отрезки ОА2 = а, ОВ2 = b – большая и малая полуоси. Величина
Пример. Найти каноническое уравнение эллипса, зная его большую полуось а = 12 и эксцентриситет e = 0,5. По определению
3. Гиперболой называется множество всех точек плоскости, абсолютное значение разности расстояний которых до двух данных точек F1 и F2 (фокусов) есть величина постоянная (2а). |F1М - F2М| = 2а. Каноническое уравнение гиперболы F1(-с, 0), F2(с, 0) – фокусы.
Отрезки ОА2 = а – действительная полуось, ОВ2 = b – мнимая полуось гиперболы.
Пример. Найти каноническое уравнение гиперболы, зная уравнения асимптот Зная F1F2 = 2с = 20, находим с = 10. Из уравнений асимптот
4. Параболой называется множество точек плоскости, равноудаленных от данной точки F, называемой фокусом и данной прямой, называемой директрисой, FM = NM.
Каноническое уравнение параболы, симметричной оси Ох, у2 = 2рх (р > 0).
Уравнение параболы, симметричной оси Оу, имеет вид: х2 = 2ру, Пример. Найти уравнение параболы, проходящей через точку А(2, 4) и симметричной оси Ох. В каноническое уравнение у2 = 2рх подставим координаты точки А: 16 = 4р, р = 4. Уравнение параболы примет вид у2 = 8х. Примеры для самостоятельной работы 1. Составить каноническое уравнение эллипса, зная его малую полуось b = 2 2. Найти координаты фокусов, полуоси и эксцентриситет гиперболы 9х2 - 16у2 = 144. 3. Найти каноническое уравнение гиперболы, проходящей через точки А (2; 1) и В(- 4; 4. Определить вид кривой у2 - 2х + 4у + 2 = 0. 5. Найти фокус и уравнение директрисы параболы у2 = 24х. ВВЕДЕНИЕ В АНАЛИЗ
Если каждому элементу x Множество Х называется областью определения функции, а множество Y – областью её значений. Существуют следующие способы задания функции: табличный, графический, аналитический, словесный. Элементарные функции делятся на алгебраические и неалгебраические (трансцендентные). К алгебраическим относятся: целая рациональная, дробно-рациональная и иррациональная функции.
|
|||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 706; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.111.24 (0.122 с.) |
 .
. вектора
вектора  называют его проекции на координатные оси Ох, Оу, Оz. Записывают
называют его проекции на координатные оси Ох, Оу, Оz. Записывают  или
или .
. координатных осей Ох, Оу, Оz.
координатных осей Ох, Оу, Оz. .
. ;
;  ;
;  ;
; .
. и
и  . При сложении векторов их одноименные координаты складываются
. При сложении векторов их одноименные координаты складываются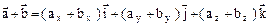
 .
. или
или  .
. равны тогда и только тогда, когда выполняются равенства
равны тогда и только тогда, когда выполняются равенства .
. , то его координаты определяются
, то его координаты определяются  .
. ;
; 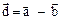 ,
,  ,
,  .
. = (1 + 3; -3 + 4; 2 + (-5)) = (4; 1; -3);
= (1 + 3; -3 + 4; 2 + (-5)) = (4; 1; -3); = (1 -3; -3 -4; 2 - (-5)) = (-2; -7; 7);
= (1 -3; -3 -4; 2 - (-5)) = (-2; -7; 7);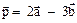 = 2 (1; - 3; 2) -3(3; 4; -5) = (2; -6; 4) - (9; 12; -15) =
= 2 (1; - 3; 2) -3(3; 4; -5) = (2; -6; 4) - (9; 12; -15) =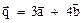 = 3 (1; -3; 2) + 4 (3; 4; -5) =
= 3 (1; -3; 2) + 4 (3; 4; -5) = .
. = (х2 -х1, у2 -у1, z2 -z1) = (-1 -9; 3-(-7); 1 -(-4)) = (-10; 10; 5);
= (х2 -х1, у2 -у1, z2 -z1) = (-1 -9; 3-(-7); 1 -(-4)) = (-10; 10; 5); =
= 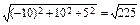 = 15.
= 15. .
. .
. .
. и
и  коллинеарны.
коллинеарны. , откуда 3a = -12; a = -4; 2b = 3, b = 3/2.
, откуда 3a = -12; a = -4; 2b = 3, b = 3/2. ;
;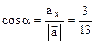 ;
;  ;
;  .
. :
: или
или  .
. - переместительный закон;
- переместительный закон; - распределительный закон;
- распределительный закон; - сочетательный закон;
- сочетательный закон; .
.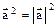 .
. и
и  . По свойствам 4 и 5 имеем
. По свойствам 4 и 5 имеем  ;
;  .
. .
. .
. .
.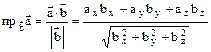 .
. , если
, если  ,
,  , угол a между векторами
, угол a между векторами  =
= = 9×9 + 12×3×4×cos60° + 4×16 =
= 9×9 + 12×3×4×cos60° + 4×16 = .
.
 .
. и
и  взаимно перпендикулярны?
взаимно перпендикулярны?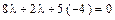 или 10l -20 = 0, l = 2.
или 10l -20 = 0, l = 2. ,
, 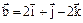 ,
,  . Найти
. Найти  ,
,  ,
,  .
. = (1; -2; 2);
= (1; -2; 2);  (10; 4; 2). Применим формулу
(10; 4; 2). Применим формулу  ,
,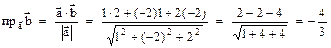 .
.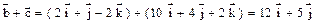 .
. .
.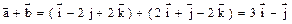 .
. .
. (3; -5; 8) и
(3; -5; 8) и  и
и  , если векторы
, если векторы  и
и  перпендикулярны.
перпендикулярны. и
и  взаимно перпендикулярны?
взаимно перпендикулярны? ,
,  . Найти скалярное произведение векторов
. Найти скалярное произведение векторов  = (7; -2; 6). Найти вектор
= (7; -2; 6). Найти вектор  , удовлетворяющий условиям:
, удовлетворяющий условиям: 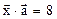 ,
,  ,
, 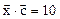 .
. = (m, n), параллельный этой прямой, то можно записать каноническое уравнение прямой
= (m, n), параллельный этой прямой, то можно записать каноническое уравнение прямой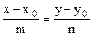 .
. = (А, В), перпендикулярный к ней, то можно записать уравнение
= (А, В), перпендикулярный к ней, то можно записать уравнение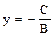 .
. .
. и
и 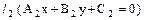 . Тогда прямые
. Тогда прямые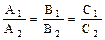 ;
;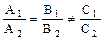 ;
;
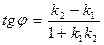 ;
; , то прямые перпендикулярны.
, то прямые перпендикулярны. .
. .
. .
.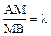 вычисляются по формулам
вычисляются по формулам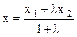 ,
, 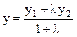 .
. .
.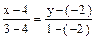 или
или 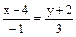 , 3х - 12 = -у - 2, 3х + у - 10 = 0.
, 3х - 12 = -у - 2, 3х + у - 10 = 0. ,
,  .
.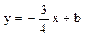 .
. ,
, и
и 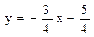 .
. . Прямые параллельны.
. Прямые параллельны.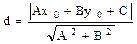 .
. .
. ,
,
 называется эксцентриситетом и характеризует вытянутость эллипса.
называется эксцентриситетом и характеризует вытянутость эллипса. , с = 6. Из соотношения b2 = а2 - с2 определим b2 = 144 - 36 = 108, тогда уравнение эллипса примет вид
, с = 6. Из соотношения b2 = а2 - с2 определим b2 = 144 - 36 = 108, тогда уравнение эллипса примет вид .
. , (b2 = c2 - a2),
, (b2 = c2 - a2),
 - асимптоты гиперболы,
- асимптоты гиперболы,  - эксцентриситет.
- эксцентриситет. и расстояние F1F2 = 20.
и расстояние F1F2 = 20. . Составим систему уравнений:
. Составим систему уравнений: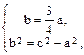
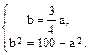
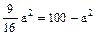 ,
,  , а2 = 64, b2 = 100 – 64 = 36. Уравнение гиперболы примет вид
, а2 = 64, b2 = 100 – 64 = 36. Уравнение гиперболы примет вид  .
.
 - фокус,
- фокус,  - директриса, р – расстояние от фокуса до директрисы.
- директриса, р – расстояние от фокуса до директрисы.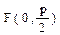 - фокус,
- фокус,  - директриса.
- директриса. и F1 F2 = 8.
и F1 F2 = 8. ).
). X ставится в соответствие определенный элемент y
X ставится в соответствие определенный элемент y 


