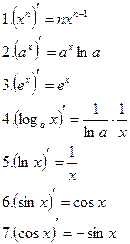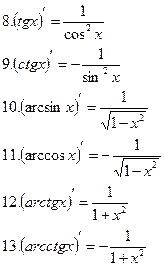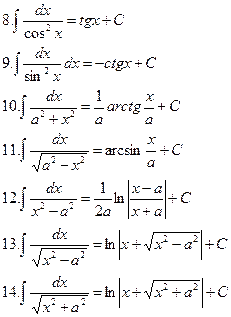Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Решение системы уравнений по формулам Крамера. ⇐ ПредыдущаяСтр 2 из 2
Исходная система уравнений имеет вид:
1. Из коэффициентов при неизвестных составляем главный определитель системы: 2. По правилу Сарруса находим значение этого определителя:
3. Заменяя столбцы коэффициентов при каждом из неизвестных в главном определителе системы столбцом свободных членов, мы находим соответствующие вспомогательные определители системы:
4. В целях рациональности вычисления находим вспомогательные определители, применяя теорему Лапласа к первому, второму, третьему столбцу, соответственно: 4.1
4.2
4.3
5. По формулам Крамера находим неизвестные:
Решение окончено. Проверка:
Ответ: ежедневный выпуск продукции составляет 200 шт. изделия S1, 150 шт. изделия S2 и 200 шт. изделия S3. Задача № 2 Определить, имеет ли матрица A обратную, и если имеет, то вычислить ее:
Решение 1) Вычисляем определитель матрицы А, применяя теорему Лапласа к первой строке:
2) Выписываем транспонированную матрицу АТ:
3) Строим присоединенную матрицу
Выписываем присоединенную матрицу: 4) Находим обратную матрицу по формуле:
Проверка. Воспользуемся определением обратной матрицы
Задача № 3 В таблице приведены данные об исполнении баланса. Используя модель Леонтьева многоотраслевой экономики, вычислить необходимый объем валового выпуска каждой отрасли, если конечный выпуск энергетической отрасли увеличится вдвое, а машиностроительной в 1,2 раза.
Решение 1) Вычисляем коэффициенты прямых затрат aij, показывающие, какой объем продукции i -ой отрасли идет на производство одной единицы продукции j -ой отрасли:
2) Выписываем столбец валового выпуска X, столбец нового конечного выпуска Y, а также матрицу прямых затрат А.
3) Вычисляем матрицу E-A
4) Вычисляем матрицу полных затрат S=(E-A)-1. Каждый элемент sij этой матрицы показывает величину валового выпуска i -ой отрасли, необходимого для обеспечения выпуска одной единицы конечного продукта j -ой отрасли.
4.1. Вычисляем определитель 4.2. Находим транспонированную матрицу 4.3. Строим присоединенную матрицу:
4.4. Находим обратную матрицу: 5) Вычисляем новый вектор валового выпуска:
6) Строим новую балансовую таблицу, предварительно вычисляя недостающие величины:
Проверка: Задача № 4 В результате маркетингового исследования установлено, что функции спроса и предложения имеют вид:
где p – цена товара. Найти: 1) Равновесную цену p0. 2) Эластичность спроса и предложения для этой цены. 3) Изменение дохода при увеличении цены на 5% от равновесной. Решение 1) Определяем равновесную цену p0, при которой спрос равен предложению.
Отсюда p0=2. (Отрицательный корень отбрасываем, как не имеющий экономического смысла).
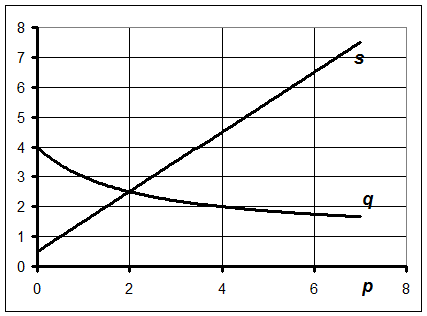
График зависимостей спроса и предложения от цены представлен на рис. 1.
Рис.1. Зависимости спроса и предложения от цены. 2) Находим эластичности спроса и предложения для равновесной цены. 2.1. Находим производные q’(p) и s’(p).
2.2. Получаем общие выражения для эластичностей спроса и предложения.
2.3. Вычисляем эластичности спроса и предложения при равновесной цене.
Таким образом, при увеличении цены на 1% от равновесного значения спрос уменьшается (т.к. «-») на 0, 3%, а предложение возрастает (т.к. «+») на 0,8%. 3) Выведем общее выражение для эластичности дохода R=pq по цене, пользуясь свойствами эластичности и подставим в него численные значения p0 и E2(q):
Это означает, что при увеличении цены на 1% от равновесного значения доход увеличивается на 0,7%. Следовательно, при увеличении цены на 5% от ее равновесного значения доход увеличится на 5×0,7%=3,5%.
Ответ: 1) равновесная цена товара равна 2; 2) при увеличении цены на 1% от равновесного значения спрос уменьшается на 0, 3%, а предложение возрастает на 0,8%; 3) при увеличении цены на 5% от ее равновесного значения доход увеличится на 3,5%.
Задача № 5 Фирма реализует произведенную продукцию по цене p, а зависимость издержек C имеет вид Используя методы дифференциального исчисления: 1) выполнить полное исследование функции зависимости прибыли фирмы П от объема производства q построить ее график. 2) Найти оптимальный для фирмы объем выпуска продукции и соответствующую ему прибыль. a=7; b=0,01; c=5; p=10 Решение Учитывая, что прибыль представляет собой разность между доходом и издержками, и подставляя численные данные, получаем явный вид зависимости прибыли от объема производства:
1) Выполняем полное исследование функции П(q) 1.1. Область определения D(П)=[0;+∞]. 1.2. Находим первую и вторую производную П’(q) и П’’(q)
1.3. Находим критические точки, решая уравнение П’(q)=0
1.4. Наносим критическую точку на числовую ось, и находим знак первой производной на каждом из получившихся интервалов:
Из рисунка делаем выводы о том, что функция возрастает при Вычислим значение функции в этой точке:
1.5. Найдем точку перегиба графика функции, решая уравнение П’’(q)=0
Так как случай q=0 не представляет практического интереса, будем считать, что график функции точек перегиба не имеет. 1.6. Найдем, на каких интервалах график функции выпуклый, а на каких—вогнутый. Так как 1.7. Сводим все полученные результаты в итоговую таблицу: Таблица 1.
1.8. Строим схематический график функции
Рис.2. График зависимости прибыли от объема выпуска продукции. 2) Очевидно, что оптимальным для фирмы является объем выпуска, равный 10, при этом прибыль будет максимальна и составит 15. Ответ в данной задаче нет необходимости выписывать отдельно, так как он фактически содержится в таблице 1. Задача №6 Производственная функция фирмы представляет собой функцию Кобба-Дугласа:
где: x —объем основных фондов в (руб.); y —объем трудовых ресурсов (чел.); z —объем выпуска продукции в (руб.); A, α, β>0 —постоянные величины, причем α+ β≤1. Известно также, что увеличения выпуска продукции на a% можно достичь или увеличением основных фондов на b% или увеличением численности работников на c%. В настоящее время один работник производит за месяц продукции на M руб., а численность работников L. Основные фонды оцениваются в K руб. Период амортизации основных фондов N месяцев, а месячная зарплата s руб. в месяц. Найдите: 1) явный вид производственной функции этой фирмы; 2) оптимальный размер фирмы, т.е. численные значения x и y, обеспечивающие максимальную прибыль. a=3, b=6, c=9, M=104, L=103, K=108, N=12, s=1000. Решение. Прежде всего установим экономический смысл параметров α и β. Для этого найдем частные эластичности выпуска по основным фондам и трудовым ресурсам. Находим
Находим частные эластичности выпуска продукции по основным фондам и трудовым ресурсам:
Таким образом, параметр α показывает, на сколько процентов изменяется выпуск продукции при увеличении объема основных фондов на 1%. Аналогично, параметр β показывает, на сколько процентов изменяется выпуск продукции при увеличении объема трудовых ресурсов предприятия на 1%.
После этих вводных замечаний приступаем к решению задачи. 1) Определим явный вид производственной функции. 1.1. Учитывая экономический смысл параметров α и β, получаем:
Производственная функция принимает вид: 1.2. Определяем параметр A. Для этого подставляем в выражение (1) известные величины M=104, L=103, K=108 и учитывая, что в настоящее время выпуск продукции равен
Таким образом, производственная функция данной фирмы имеет вид:
2) Определим оптимальный размер фирмы. В качестве критерия оптимизации выбираем прибыль, т.е. оптимальным будем считать такой размер фирмы, при котором ее прибыль максимальна. Выражение для прибыли (разность между доходами и издержками) имеет вид:
где: p1 -себестоимость одной единицы основных фондов, p2 -себестоимость одной единицы трудовых ресурсов. По условию задачи Таким образом, задача свелась к нахождению максимума функции двух переменных:
который находится по общим правилам дифференциального исчисления. 2.1. Находим все частные производные функции (4) первого и второго порядка:
2.2. Находим критические точки функции, приравнивая первые частные производные к нулю и решая получившуюся систему уравнений:
Выражаем
Отсюда Поставляя найденное значение y в первое уравнение, находим x:
Итак, точка Однако равенство нулю частных производных первого порядка является необходимым, но совсем не достаточным условием экстремума функции двух переменных. Для ответа на этот вопрос следует воспользоваться достаточным признаком экстремума, что и будет сделано в следующем пункте. 2.3. Вычисляем значения вторых производных в критической точке:
2.4. Вычислим оптимальный объем выпуска продукции z0 и оптимальную прибыль
Ответ: оптимальными для данной фирмы являются: объем основных фондов 1,44×108 руб, численность работников 8×103 чел. При этом прибыль будет максимальна и составит 4×106 руб при объеме выпуска продукции, равном 2,4×107 руб Задача №7 Задача Кобба – Дугласа вычиление объёма продукции или инвестиций. Инвестор вложил в производство R0 тыс.руб. и в течение n лет планирует непрерывно увеличивать объем инвестиций на a тыс. руб. ежегодно. Ожидаемая доходность инвестиций составляет i% годовых. Определите 1) современную стоимость такого проекта по формуле 2) наращенную сумму такого потока платежей по формуле Примечание: Современная (текущая, капитализированная) стоимость является одним из важнейших понятий в количественном анализе финансовых операций. Большинство аналитических методов оценки эффективности инвестиционных проектов, кредитных операций основаны именно на определении этой величины. Наращением или ростом денежной суммы называют процесс увеличения суммы денег в связи с присоединением процентов. R0=10; a=2; n=3; i=8 Решение. 1) Подставляя численные значения величин, получаем:
где использованы обозначения 1.1. Вычислим интеграл Введем новую переменную Для нахождения новых пределов интегрирования составим таблицу:
В результате получаем:
1.2. Вычислим интеграл Суть метода заключается в использовании формулы Сравнивая интеграл I2 c этой формулой, замечаем, что Отсюда В последнем интеграле делаем замену переменных В результате:
Подставляем полученные выражения для u, du, v, dv в формулу интегрирования по частям, получаем
1.3. 2) Замечание. В указанных в данном учебном пособии приложениях таблица значений функции у=ех дана с шагом 0,1. Если этой точности недостаточно для решения заданного Вам варианта задания необходимо использовать инженерные калькуляторы или воспользоваться микрокалькулятором с шагом менее 0,1. Ответ: Современная стоимость инвестиционного проекта составляет приблизительно 34,35 тыс. руб., а наращенная за три года сумма приблизительно равна 43,667 руб.
Задача №8 Нахождение общего решения дифференциального уравнения, раскрывающего зависимость спроса и предложения товара от цены.
1. Q(p)= q0 – q1p(t) - зависимость спроса от цены S(p)= s0 – s1 p(t) - зависимость предложения от цены q0 =10, q1 =2, Q(p)= 10-2p(t) s0 = -4, s1=4, S(p)=-4+4p(t) Начальная цена: p(0)= p0=2
Дифференциальное уравнение зависимости цены от времени:
2. Подставляя численные данные, получаем:
Начальные условия p(0)=2 (3). Имеем задачу линейного неоднородного дифференциального уравнения Коши для первого порядка. 3. Найдём решение (2) в виде: р=uv; р´=u´v+ u v´, т.е. Подставляем (4) в (2)
4. Полагаем 5. Решаем (5)
Полагаем, что С=1, тогда ln 1=0 и ln │u│=-3t, и = е- 3 t (7) 6. Подставляя (7) в (6) получим е- 3 t
7. Подставляя (7) и (8) в р=uv, получаем: р = е- 3 t ( р = Найдём С, используя начальное условие p(0)=2. 2 = p(t) = 8. Найдём равновесную цену р*: Q(p*) = S(p*); 10-2 р* =-4+4 р*; 14=6 р*, р* =2 Решение можно записать в виде p(t) = р* - Примечание р0 - р* =2- Следовательно (*) имеет вид: p(t) = р* + (р0 - р*) е- 3 t .
Приложения Таблица производных
Таблица интегралов
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 219; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.190.113 (0.138 с.) |




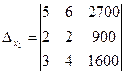
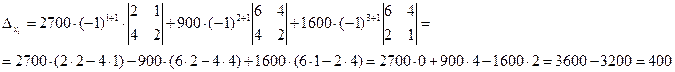

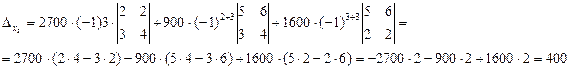
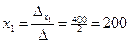







 . Ее элементы представляют собой алгебраические дополнения соответствующих элементов транспонированной матрицы АТ.
. Ее элементы представляют собой алгебраические дополнения соответствующих элементов транспонированной матрицы АТ.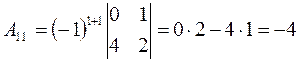





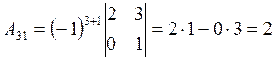
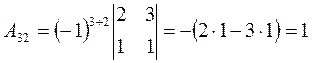

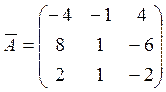
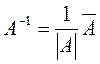

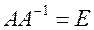 :
:

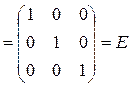

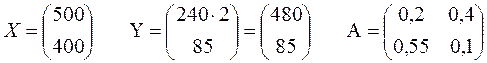
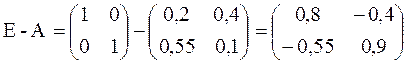
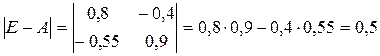
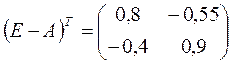
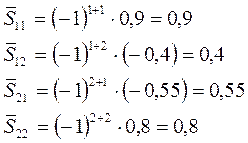


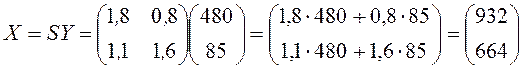
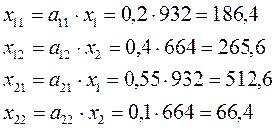

 - спроса,
- спроса,
 - предложения,
- предложения,




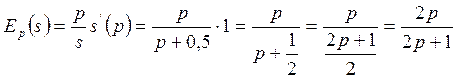


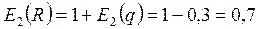
 , где q - объём производства.
, где q - объём производства.





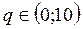 , а убывает при
, а убывает при 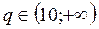 ; в точке q=10 функция имеет максимум.
; в точке q=10 функция имеет максимум.
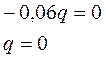
 на всей области определения, делаем вывод о том, что график функции выпуклый на всей области определения.
на всей области определения, делаем вывод о том, что график функции выпуклый на всей области определения.
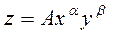
 и
и  :
:

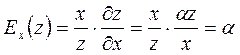

 ,
,
 (1)
(1) , получаем следующее уравнение для определения A:
, получаем следующее уравнение для определения A: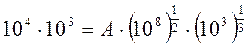 , откуда A=100.
, откуда A=100. (2)
(2)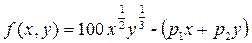 , (3)
, (3)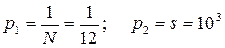
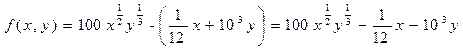 , (4)
, (4)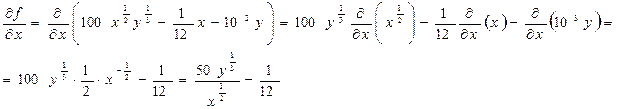
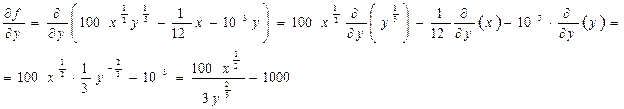




 из первого уравнения и подставляем во второе. Получаем:
из первого уравнения и подставляем во второе. Получаем: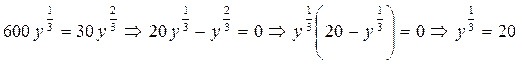
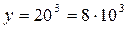

 является критической точкой функции прибыли данной задачи.
является критической точкой функции прибыли данной задачи. Вычисляем определитель:
Вычисляем определитель: Поскольку a<0, D>0, то на основании достаточного признака экстремума функции двух переменных делаем вывод о том, что точка
Поскольку a<0, D>0, то на основании достаточного признака экстремума функции двух переменных делаем вывод о том, что точка  является точкой максимума функции прибыли. Следовательно, это и есть оптимальный размер фирмы.
является точкой максимума функции прибыли. Следовательно, это и есть оптимальный размер фирмы.


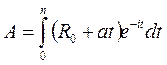 .
.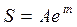


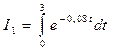 , используя метод замены переменной.
, используя метод замены переменной. , тогда
, тогда 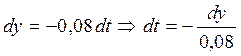 .
.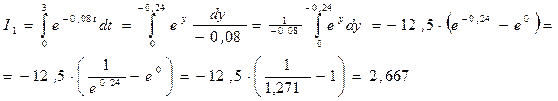
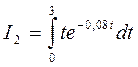 , применяя метод интегрирования по частям.
, применяя метод интегрирования по частям.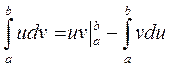 .
.
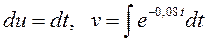 .
.

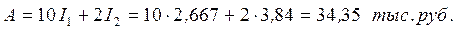

 к(Q(p(t))- S(p(t))) (1), к=0,5
к(Q(p(t))- S(p(t))) (1), к=0,5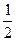 (10-2р+4-4р),
(10-2р+4-4р),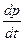 =7-3р;
=7-3р; 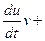
 ; (4)
; (4)
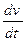 -7=0
-7=0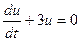 , тогда
, тогда 
 =-3 и;
=-3 и; 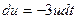 ;
; 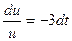 ;
; , ln │u│=-3t+ ln C.
, ln │u│=-3t+ ln C. , проинтегрируем обе части уравнения,
, проинтегрируем обе части уравнения,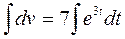 , получим v =7*
, получим v =7*  e3t +C или v =
e3t +C или v = 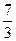 e3t +C (8)
e3t +C (8) e3t +C), р =
e3t +C), р =  е- 3 t e3 t + С е- 3 t,
е- 3 t e3 t + С е- 3 t,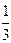 =С.
=С. е- 3 t .
е- 3 t .