
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Знакопеременные и знакочередующиеся ряды
10. Признак Лейбница. Пусть дан знакочередующийся ряд 11. Пусть дан знакопеременный ряд 12. Если знакопеременный ряд Функциональные ряды Основные понятия 13. Ряд 14. Областью абсолютной сходимости данного функционального ряда называется множество значений х, при которых данный ряд сходиться как числовой ряд. 15. Область абсолютной сходимости функционального ряда находится из неравенства 16. Степенным рядом называется ряд вида 17. Радиус абсолютной сходимости степенного ряда: 18. Интервалом абсолютной сходимости степенного ряда называется интервал вида (a – R; a + R). 19. Интервал абсолютной сходимости с исследованными границами называется областью абсолютной сходимости степенного ряда. 20. Теорема Абеля: 1) если степенной ряд сходится при значении 21. Основные свойства степенных рядов в интервале (a – R; a + R) абсолютной сходимости: 1) В интервале (a – R; a + R) сумма ряда есть непрерывная функция. 2) Степенной ряд в каждой точке интервала (a – R; a + R) можно почленно дифференцировать бесконечное число раз. 3) Степенной ряд можно почленно интегрировать по любому интервалу 22. Ряд Тейлора для функции 23. Частный случай ряда Тейлора для функции 24. Разложение основных функций в ряд Маклорена:
25. Тригонометрическим называется функциональный ряд вида 26. Ряд Фурье для функции 27. Если 28. Если 29. Условия Дирихле. Функция
30. Ряд Фурье для функции 31. Если 32. Если
|
|||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 158; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.105.124 (0.009 с.) |
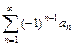 , где an > 0. Если 1) члены знакочередующегося ряда убывают по абсолютной величине
, где an > 0. Если 1) члены знакочередующегося ряда убывают по абсолютной величине 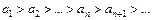 и 2) предел его общего члена при
и 2) предел его общего члена при  равен нулю, т. е.
равен нулю, т. е. 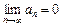 , то исходный ряд сходится, а его сумма не превосходит первого члена
, то исходный ряд сходится, а его сумма не превосходит первого члена 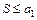 .
.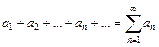 . Если соответствующий ряд
. Если соответствующий ряд 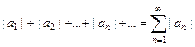 сходится, то данный ряд сходится абсолютно.
сходится, то данный ряд сходится абсолютно.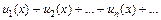 , членами которого являются функции, называется функциональным.
, членами которого являются функции, называется функциональным.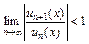 .
.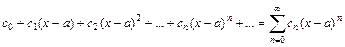 .
.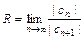 или
или 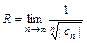 .
.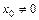 , то он сходится и притом абсолютно при всех значениях х таких, что | x | < | x 0|; 2) если степенной ряд расходится при х 1, то он расходится при всех значениях х таких, что | x | > | x 1|.
, то он сходится и притом абсолютно при всех значениях х таких, что | x | < | x 0|; 2) если степенной ряд расходится при х 1, то он расходится при всех значениях х таких, что | x | > | x 1|.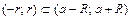 .
.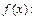
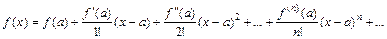
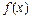 при а = 0 – ряд Маклорена:
при а = 0 – ряд Маклорена: 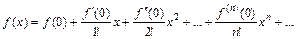

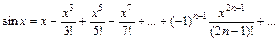
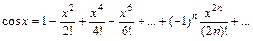
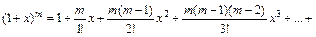
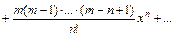
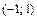
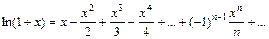
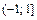

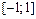
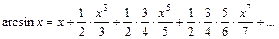
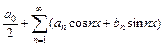 .
.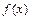 периода 2p:
периода 2p: 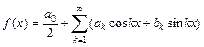 , где
, где 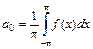 ,
, 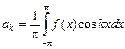 и
и 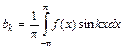 .
.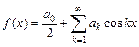 , где
, где 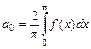 ,
, 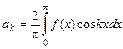 и
и 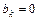 .
.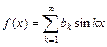 , где
, где 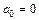 ,
, 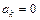 и
и 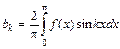 .
.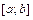 ограничена и
ограничена и 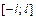 :
: 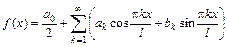 , где
, где  ,
, 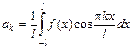 и
и 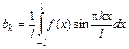 .
.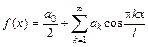 , где
, где 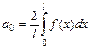 ,
, 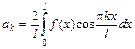 и
и 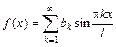 , где
, где 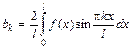 .
.


