
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дифференциальное исчисление. Производная
Определение производной. Правила дифференцирования.
Правила дифференцирования 1. 2. 3. 4.
Примеры.
Найти производную функции, пользуясь определением.
1) 2) 3) 4) 5) 6) х0 – произвольно выбранная точка. х=0 – только правостороннюю производную.
7) 8) 9) 10) 12)
Формулы дифференцирования. техника дифференцирования Таблица производных
Примеры. Найти производные функций 1) 4)
Решение:
1)
2)
3)
4)
5)
Задания для самостоятельной работы
Найти производные функций
ПРИЛОЖЕНИЕ ПРОИЗВОДНОЙ. Применение производной при нахождении пределов. Правило Лопиталя (для неопределенностей вида Предел отношения функций равен пределу отношения производных этих функций, если предел отношения производных существует. Примеры. 1.
2.
3.
4.
5.
Раскрытие неопределенностей вида Вычисление пределов функций можно осуществлять при помощи преобразования
В силу непрерывности показательной функции:
Пример
Задания для самостоятельной работы 1)
3)
5)
Экстремумы функции (локальные). Справочный материал. Определение 1. Функция
Определение 2. Функция Возрастающие и убывающие функции называются монотонными, а промежутки, в которых функция возрастает или убывает,- промежутками монотонности. Возрастание и убывание функции
Определение 3. Внутренние точки области определения функции Производная Теперь мы можем сформулировать ПРАВИЛО нахождения интервалов монотонности функции 1. Находим область определения функции 2. Вычисляем производную 3. Критическими точками и точками разрыва функции разбиваем область определения функции 4. Исследуем знак Пример 4.1. Найти интервалы монотонности функции
РЕШЕНИЕ: 1. 2. Найдём критические точки
Последующие рассуждения удобно представить в виде табл.4.1. Таблица 4.1
О т в е т. На интервалах
Дадим определение точек локального (местного) минимума и максимума. Такие точки называют точками локального экстремума данной функции, а значения функции в этих точках- локальным максимумом (минимумом) функции или локальным экстремумом функции. Точка На рис. 4.2 точки
Обратите внимание на локальный характер изучаемых свойств функции: в точке Теорема. Если точка На рис.2 в точках Сформулированные выше условия являются лишь необходимыми для существования экстремума. Они позволяют только выделить точки, в которых функция может иметь экстремум. Это значит, что экстремум может быть только в критических точках, но не всякая критическая точка является точкой экстремума. Сформулируем достаточное условие существования экстремума в критической точке
рис. 4.3
Пусть функция Тогда: а) если б) если в) если существует такая окрестность точки Замечание. Требование непрерывности
График этой функции дан на рис. 4.3. По графику видно, что функция в точке Пример 4.2. Исследовать на экстремум функцию РЕШЕНИЕ: Область определения функции Найдём интервалы монотонности функции (см. пример 4.1).
Составим табл. 4.2.
При переходе через точку
Ответ: max f (x) = f (2)= 20; min f (x) = f (4) = 16.
Рис.4.4 Пример 4.3. Исследовать на экстремум функцию
РЕШЕНИЕ.
Производная Составим табл. 4.3.
Ответ: min
Пример 4.4. Найти экстремум и интервалы монотонности функции
РЕШЕНИЕ
В данном случае
Составим табл.4.4, которая является о т в е т о м на поставленную задачу.
Обратите внимание при построении графика: а) если в точке экстремума б) если в точке экстремума Эскиз графика функции
Рис.4.6 Примеры. 1. Найти промежутки монотонности функции: 1) РЕШЕНИЕ: 1) I.сп. а) б) в) г) д) Заполним таблицу монотонности
Функция II.сп. а) б) в) г)
2) а) б) в) функция убывает в промежутках
3) а) б)
учитывая область определения, имеем: функция в) с учётом области определения получаем: функция В точках 2. Дана функция: 1) 1) а) б) в) г) Заполним таблицу монотонности
Функция В точке
2)
а)
б)
в)
г) Заполним таблицу монотонности
функция
В точках x =0 и x =-4 функция определена и непрерывна, поэтому эти точки включаются в промежутки монотонности;
д) найдём точки пересечения графика с осями координат.
е) построим график функции
Задания для самостоятельной работы
Исследуйте функцию на возрастание (убывание) и экстремумы: А. 1) 5) Б. 1) 4) В. 1) 4)
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 368; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.98.13 (0.154 с.) |





 , х>0
, х>0 ,
, 
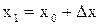 ,
, 



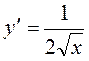 для х>0, т.к.
для х>0, т.к.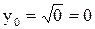
 ,
, 
 .
. 11)
11)  .
. .
. существует, но функция не дифференцируется, т.е. не имеет конечной производной.
существует, но функция не дифференцируется, т.е. не имеет конечной производной. где c-константа
где c-константа








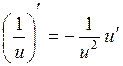



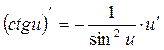


 2)
2)  3)
3) 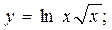
 5)
5) 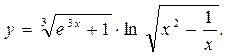

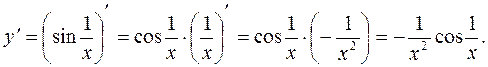



 2)
2)  3)
3)  4)
4) 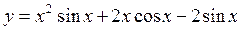 5)
5) 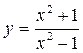 6)
6)  7)
7)  8)
8)  9)
9) 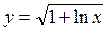 10)
10)  11)
11)  12)
12)  13)
13)  14)
14)  15)
15) 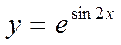 16)
16) 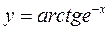 17)
17)  18)
18) 
 20)
20)  21)
21) 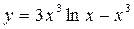 22)
22)  23)
23)  24)
24)  25)
25) 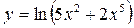 26)
26)  27)
27) 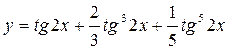 28)
28)  29)
29)  30)
30) 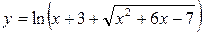 31)
31)  32)
32)  33)
33)  34)
34) 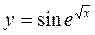 35)
35)  36)
36) 
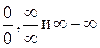 )
)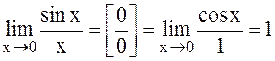







 ,
,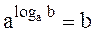 - логарифмическое тождество.
- логарифмическое тождество.

 2)
2) 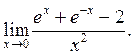
 4)
4) 
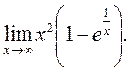 6)
6) 
 называется возрастающей на множестве
называется возрастающей на множестве 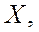 если для любых
если для любых  и
и  выполняется условие
выполняется условие 
 называется убывающей на множестве
называется убывающей на множестве  если для любых
если для любых  из
из 
 для всех x из
для всех x из  то
то  для всех
для всех  то
то  равна 0 или не существует, называются критическими точками этой функции.
равна 0 или не существует, называются критическими точками этой функции.
 на интервалы, на каждом из которых производная сохраняет знак, т.е. интервалы знакопостоянства
на интервалы, на каждом из которых производная сохраняет знак, т.е. интервалы знакопостоянства 
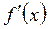 на каждом из интервалов знакопостоянства. Если на рассматриваемом интервале
на каждом из интервалов знакопостоянства. Если на рассматриваемом интервале  то на этом интервале
то на этом интервале  возрастает, если же
возрастает, если же  то на этом интервале
то на этом интервале 

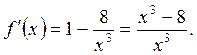

 но
но  поэтому не является критической точкой, а является точкой разрыва функции. Итак, имеем одну критическую точку
поэтому не является критической точкой, а является точкой разрыва функции. Итак, имеем одну критическую точку  и точку разрыва функции
и точку разрыва функции 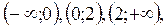 в которых
в которых 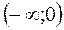 и
и  функция возрастает, на
функция возрастает, на  убывает (рис. 4.1).
убывает (рис. 4.1). Рис.4.1
Рис.4.1 из области определения функции
из области определения функции  из этой окрестности выполняется неравенство
из этой окрестности выполняется неравенство  т.е.
т.е. 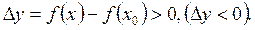
 точки локального максимума функции
точки локального максимума функции  на
на  а точки
а точки  локального минимума.
локального минимума. рис. 4.2
рис. 4.2 функция принимает наибольшее значение только вблизи точки
функция принимает наибольшее значение только вблизи точки  больше, чем в точке максимума
больше, чем в точке максимума 
 является точкой локального экстремума функции
является точкой локального экстремума функции  , определённой в некоторой окрестности точки
, определённой в некоторой окрестности точки  , то производная в точке
, то производная в точке  касательные к графику параллельны оси
касательные к графику параллельны оси  т.е. производные в этих точках равны 0. В точке
т.е. производные в этих точках равны 0. В точке 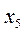 касательная перпендикулярна оси
касательная перпендикулярна оси  не существует; в точке
не существует; в точке  нельзя провести касательную (есть левая и правая касательные, но они сливаются в одну). Значит,
нельзя провести касательную (есть левая и правая касательные, но они сливаются в одну). Значит,  не существует.
не существует.


 и в некоторой её окрестности и имеет в этой окрестности производную за исключением, быть может, самой точки
и в некоторой её окрестности и имеет в этой окрестности производную за исключением, быть может, самой точки 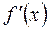 при переходе через точку
при переходе через точку 
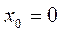 терпит разрыв первого рода. Точка
терпит разрыв первого рода. Точка  и интервалом убывания
и интервалом убывания  функции, т.е. при переходе через
функции, т.е. при переходе через 
 Критические точки:
Критические точки:  или
или  Производная
Производная  существует во всей области
существует во всей области  Теперь найдём значения
Теперь найдём значения  , при которых производная равна 0:
, при которых производная равна 0:  или
или  Критические точки
Критические точки 

 сменила знак с + на –, значит, в этой точке функция имеет максимум:
сменила знак с + на –, значит, в этой точке функция имеет максимум:  При переходе через точку
При переходе через точку  производная
производная  На рис.4.4 представлен эскиз графика функции
На рис.4.4 представлен эскиз графика функции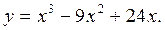

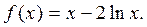
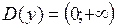 ;
;  ;
; 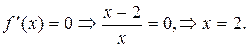
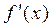 не существует, если
не существует, если  , но
, но  Таким образом, имеем одну критическую точку
Таким образом, имеем одну критическую точку 
 (рис. 4.5).
(рис. 4.5).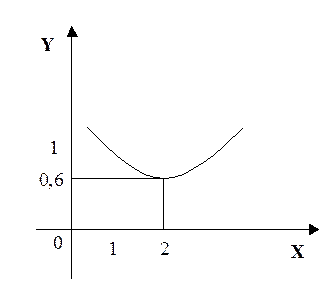 Рис.4.5
Рис.4.5
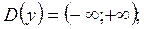
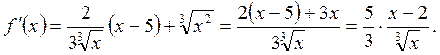
 при
при 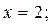
 не существует при
не существует при 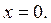 Имеем две критические точки:
Имеем две критические точки:  и
и 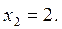
 min
min
 то экстремум “круглый” (касательная параллельна оси
то экстремум “круглый” (касательная параллельна оси  );
); представлен на рис.4.6.
представлен на рис.4.6.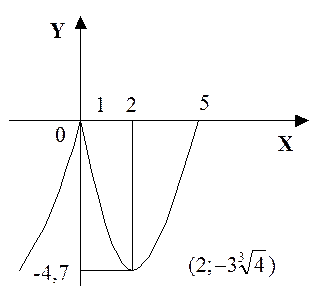
 2)
2) 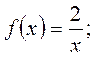 3)
3) 
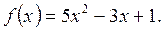

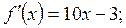
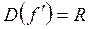

 критическая точка функции;
критическая точка функции; убывает в промежутке
убывает в промежутке  а возрастает в промежутке
а возрастает в промежутке  (точка
(точка  включается в промежутки монотонности, так в этой точке функция определена и непрерывна).
включается в промежутки монотонности, так в этой точке функция определена и непрерывна).

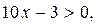
 функция возрастает в промежутке
функция возрастает в промежутке 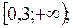

 функция убывает в промежутке
функция убывает в промежутке 



 при
при 


 и
и 
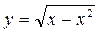





 при
при 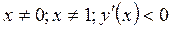 при
при 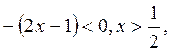
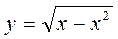 убывает в промежутке
убывает в промежутке 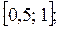
 при
при 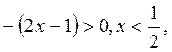
 возрастает в промежутке
возрастает в промежутке 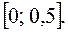
 и
и  функция определена и непрерывна, поэтому эти точки включаются в промежутки монотонности.
функция определена и непрерывна, поэтому эти точки включаются в промежутки монотонности. 2)
2) 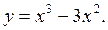 Найти её критические точки, промежутки монотонности, точки экстремума, экстремумы функции. Построить график функции
Найти её критические точки, промежутки монотонности, точки экстремума, экстремумы функции. Построить график функции 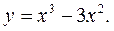



 критическая точка функции;
критическая точка функции;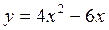 возрастает в промежутке
возрастает в промежутке  и убывает в промежутке
и убывает в промежутке 

 функция
функция 
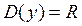 ;
;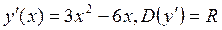 ;
;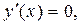

 - критические точки функции;
- критические точки функции; возрастает в промежутках
возрастает в промежутках  и
и  ; убывает в промежутке
; убывает в промежутке 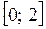 ;
;
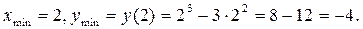


 (рис. 4.7)
(рис. 4.7) Рис.4.7
Рис.4.7 2)
2)  3)
3) 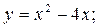 4)
4) 
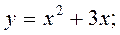 6)
6) 
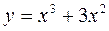 ; 2)
; 2)  ; 3)
; 3)  ;
; ; 5)
; 5) 
 ; 2)
; 2)  ; 3)
; 3)  ;
; ; 5)
; 5) 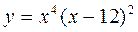 ; 6)
; 6) 



