
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Функции нескольких переменных
Частные производные Программные вопросы 1. Определение функции нескольких переменных. 2. Предел функции двух переменных и ее непрерывность. 3. Частные производные первого порядка. 4. Частные производные функции двух переменных второго и более высоких порядков. Решение типового примера
Пример 9.1. Найти частные производные первого и второго порядка функции
Решение. Найдем производные первого порядка. При нахождении производной по переменной
При нахождении производной по переменной
Находим частные производные второго порядка. Для наглядности перепишем уже найденные частные производные первого порядка:
Для нахождения второй частной производной по переменной
Аналогично, чтобы найти вторую частную производную по переменной
Найдем смешанные производные
Для нахождения
Так как
Задачи контрольной работы В заданиях 9.1.1-9.1.20 найти для заданных функций частные производные первого и второго порядков.
9.1.1. 9.1.3. 9.1.5. 9.1.7. 9.1.9. 9.1.11. 9.1.13. 9.1.15. 9.1.17. 9.1.19.
Производная по направлению Программные вопросы 1. Определение производной по направлению вектора. 2. Связь производной по направлению с частными производными. 3. Формула для нахождения производной функции в заданной точке по направлению вектора.
Решение типового примера Пример 9.2. Найти производную от функции
Решение. Производную от функции
где
Вычислим длину вектора
Следовательно, направляющие косинусы будут равны:
Далее находим все частные производные первого порядка от заданной функции
Вычислим значения этих частных производных в точке
Затем подставим полученные значения в формулу для нахождения производной по направлению в заданной точке:
Ответ. Производная от функции
Задачи контрольной работы В заданиях 9.2.1-9.2.20 найти производную от функции 9.2.1. 9.2.2. 9.2.3. 9.2.4. 9.2.5. 9.2.6. 9.2.7. 9.2.8. 9.2.9. 9.2.10. 9.2.11. 9.2.12. 9.2.13. 9.2.14. 9.2.15. 9.2.16. 9.2.17. 9.2.18. 9.2.19. 9.2.20. Градиент Программные вопросы 1. Определение градиента скалярного поля. 2. Формула для нахождения градиента функции в заданной точке. 3. Свойства градиента. Решение типового примера Пример 9.3. Найти градиент функции Решение. Градиент функции в точке
Сначала найдем все частные производные первого порядка от заданной функции:
Далее вычислим значения этих частных производных первого порядка в точке
Подставляя найденные значения в формулу градиента, получаем:
Находим его длину:
Ответ. Градиент функции Задачи контрольной работы В заданиях 3.1-3.20 найти градиент функции
9.3.1. 9.3.3. 9.3.5. 9.3.7. 9.3.9. 9.3.11. 9.3.13. 9.3.15. 9.3.17. 9.3.19.
|
|||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 371; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.156.250 (0.039 с.) |
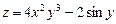 .
. , переменная
, переменная  считается константой, а любую константу можно вынести за знак производной, следовательно, производная по переменной
считается константой, а любую константу можно вынести за знак производной, следовательно, производная по переменной  . Так как переменная
. Так как переменная  является константой и его производная будет равна нулю:
является константой и его производная будет равна нулю: 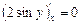 . Таким образом, частная производная заданной функции по переменной
. Таким образом, частная производная заданной функции по переменной 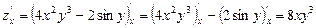 .
. :
:  . Частная производная по переменной
. Частная производная по переменной 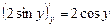 . Тогда частная производная заданной функции по переменной
. Тогда частная производная заданной функции по переменной  .
. ,
, .
.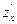 еще раз продифференцировать по переменной
еще раз продифференцировать по переменной 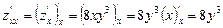 .
. снова по переменной
снова по переменной  .
.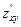 и
и  . Для того, чтобы найти
. Для того, чтобы найти  .
.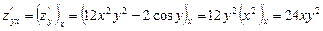 .
. . 9.1.2.
. 9.1.2.  .
. . 9.1.4.
. 9.1.4. 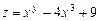 .
. . 9.1.6.
. 9.1.6.  .
. . 9.1.8.
. 9.1.8. 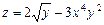 .
.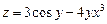 . 9.1.10.
. 9.1.10.  .
.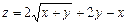 . 9.1.12.
. 9.1.12.  .
.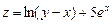 . 9.1.14.
. 9.1.14. 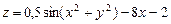 .
. . 9.1.16.
. 9.1.16.  .
. . 9.1.18.
. 9.1.18.  .
. . 9.1.20.
. 9.1.20. 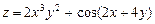 .
.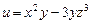 в точке
в точке  по направлению вектора
по направлению вектора 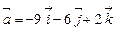 .
. в заданной точке
в заданной точке  по направлению вектора
по направлению вектора 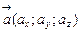 можно найти по формуле:
можно найти по формуле: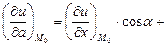

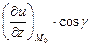 ,
,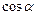 ,
,  ,
,  - направляющие косинусы вектора
- направляющие косинусы вектора 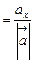 ;
; 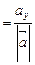 ;
; 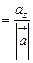 .
. :
: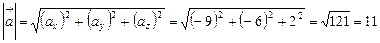 .
. ;
; 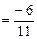 ;
; 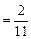 .
. ;
; 
 ;
;  .
.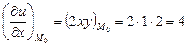 ,
, ,
,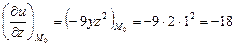 .
.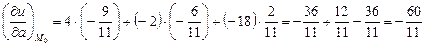 .
.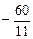 .
.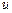 в точке
в точке 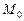 по направлению вектора
по направлению вектора  ,
, 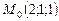 ,
,  .
.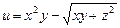 ,
, 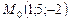 ,
,  .
.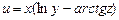 ,
, 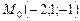 ,
,  .
.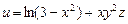 ,
,  ,
, 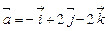 .
.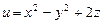 ,
,  ,
, 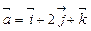 .
. ,
,  ,
,  .
. ,
,  ,
,  .
. ,
, 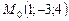 ,
,  .
.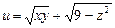 ,
,  ,
,  .
.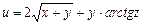 ,
,  ,
,  .
. ,
, 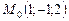 ,
, 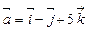 .
. ,
,  ,
,  .
. ,
,  ,
,  .
.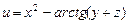 ,
, 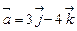 .
. ,
,  ,
,  .
.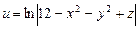 ,
,  ,
,  ,
,  ,
,  .
. ,
,  ,
,  .
.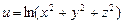 ,
,  .
.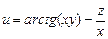 ,
,  ,
,  в точке
в точке  и его длину.
и его длину. .
. ;
;  ;
;  .
. ,
,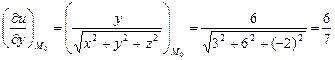 ,
, .
. .
.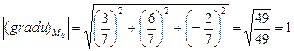 .
.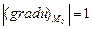 .
. ,
,  . 9.3.2.
. 9.3.2.  ,
,  .
. ,
,  . 9. 3.4.
. 9. 3.4.  ,
, 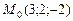 .
. ,
,  . 9.3.6.
. 9.3.6. 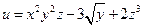 ,
,  .
.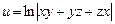 ,
,  9.3.8.
9.3.8. 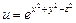 ,
,  .
.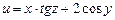 ,
, 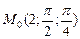 . 9.3.10.
. 9.3.10.  ,
,  .
.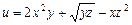 ,
,  . 9.3.12.
. 9.3.12.  ,
, 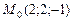 .
.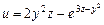 ,
,  9.3.14.
9.3.14. 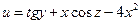 ,
,  .
.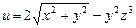 ,
,  . 9.3.16.
. 9.3.16.  ,
,  .
. ,
, 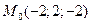 . 9.3.18.
. 9.3.18.  ,
,  .
. ,
,  . 9.3.20.
. 9.3.20.  ,
,  .
.


