Это линейные уравнения вида (1) из предыдущего параграфа, у которых в левой его части функции 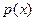 и
и  , стоящие множителями при
, стоящие множителями при  и
и 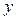 , являются постоянными, т.е. числами. Таким образом, линейными дифференциальными уравнениями второго порядка с постоянными коэффициентами называются уравнения вида
, являются постоянными, т.е. числами. Таким образом, линейными дифференциальными уравнениями второго порядка с постоянными коэффициентами называются уравнения вида
(1) 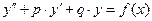 ,
,
где 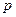 и
и 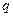 − произвольные числа, а
− произвольные числа, а 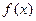 − непрерывная на некотором интервале
− непрерывная на некотором интервале  функция. Поскольку уравнение (1) является частным случаем общего линейного дифференциального уравнения 2-го порядка, то к нему применимы оба правила (Правило 1 и Правило 2) о структуре решений однородного и неоднородного уравнения, сформулированные в предыдущем параграфе.
функция. Поскольку уравнение (1) является частным случаем общего линейного дифференциального уравнения 2-го порядка, то к нему применимы оба правила (Правило 1 и Правило 2) о структуре решений однородного и неоднородного уравнения, сформулированные в предыдущем параграфе.
Для удобства мы будем рассматривать уравнения чуть более общего вида, у которого при второй производной 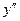 тоже стоит произвольный числовой коэффициент:
тоже стоит произвольный числовой коэффициент:
(2) 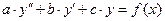 ,
,
где a, b и с – произвольные числа. Уравнение (1) является частным случаем уравнения (2) (при  ,
, 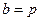 и
и 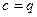 ). С другой стороны, если разделить обе части уравнения (2) на
). С другой стороны, если разделить обе части уравнения (2) на  , то коэффициент при
, то коэффициент при 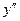 тоже станет равным 1, а потому получится уравнение вида (1). Поэтому уравнение вида (2) тоже называется линейным дифференциальным уравнением второго порядка с постоянными коэффициентами и к нему тоже применимы оба правила (Правило 1 и Правило 2) о структуре решений однородного и неоднородного уравнения, сформулированные в предыдущем параграфе.
тоже станет равным 1, а потому получится уравнение вида (1). Поэтому уравнение вида (2) тоже называется линейным дифференциальным уравнением второго порядка с постоянными коэффициентами и к нему тоже применимы оба правила (Правило 1 и Правило 2) о структуре решений однородного и неоднородного уравнения, сформулированные в предыдущем параграфе.
Рассмотрим сначала однородное уравнение, когда функция 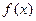 в правой части уравнения (2) равна 0:
в правой части уравнения (2) равна 0:
(3) 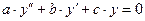 .
.
Правило 1, сформулированное в предыдущем параграфе, говорит о том, что для нахождения общего решения однородного уравнения (3) достаточно найти любые два его линейно независимых решения 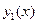 и
и 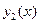 и выписать формулу для общего решения:
и выписать формулу для общего решения:
(4) 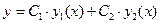 ,
,
где  и
и 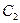 − произвольные постоянные.
− произвольные постоянные.
Как же найти эти два линейно независимых решения 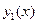 и
и 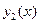 уравнения (3)? Для начала по виду уравнения (3) строится соответствующее ему квадратное уравнение, которое получается из (3) заменой
уравнения (3)? Для начала по виду уравнения (3) строится соответствующее ему квадратное уравнение, которое получается из (3) заменой 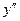 на
на 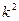 ,
,  на
на  , а
, а  на
на 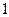 :
:
(5) 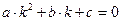 .
.
Квадратное уравнение (5) называется характеристическим уравнением для дифференциального уравнения (3). Как известно, для нахождения его корней сначала вычисляется дискриминант квадратного уравнения:
(6) 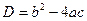 .
.
Если 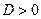 , то характеристическое уравнение (5) имеет два различных корня
, то характеристическое уравнение (5) имеет два различных корня  и
и 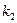 , вычисляемых по известным формулам корней квадратного уравнения:
, вычисляемых по известным формулам корней квадратного уравнения:
(7)  .
.
Если же 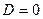 , то характеристическое уравнение имеет один корень
, то характеристическое уравнение имеет один корень  (или два совпадающих корня
(или два совпадающих корня  =
= 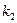 ), который получается из формулы (7) при
), который получается из формулы (7) при 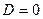 :
:
(8) 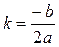 .
.
Если же дискриминант 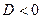 , то характеристическое уравнение (5) не имеет корней (в области действительных чисел). Вид линейно независимых решений
, то характеристическое уравнение (5) не имеет корней (в области действительных чисел). Вид линейно независимых решений 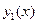 и
и 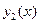 уравнения (3), входящих в формулу общего решения этого уравнения (4), устанавливает следующая
уравнения (3), входящих в формулу общего решения этого уравнения (4), устанавливает следующая
Теорема 1. Линейно независимые решения 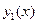 и
и 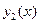 уравнения (3), входящие в формулу общего решения этого уравнения (4), имеют следующий вид в зависимости от вида корней характеристического уравнения (5).
уравнения (3), входящие в формулу общего решения этого уравнения (4), имеют следующий вид в зависимости от вида корней характеристического уравнения (5).
1. Характеристическое уравнение (5) имеет 2 различных корня  и
и 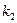 (
(
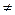
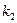 ), вычисляемых по формулам (7). Это соответствует случаю, когда дискриминант
), вычисляемых по формулам (7). Это соответствует случаю, когда дискриминант  в (6). Тогда в формуле (4)
в (6). Тогда в формуле (4) 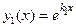 и
и 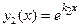 , а потому общее решение однородного уравнения (3) имеет вид:
, а потому общее решение однородного уравнения (3) имеет вид:
(9) 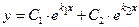 .
.
2. Характеристическое уравнение (5) имеет только один корень  , вычисляемый по формуле (8). Можно в этом случае говорить и о двух равных корнях
, вычисляемый по формуле (8). Можно в этом случае говорить и о двух равных корнях 

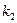 этого уравнения, что соответствует случаю
этого уравнения, что соответствует случаю 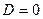 в (6). Тогда в формуле (4)
в (6). Тогда в формуле (4) 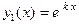 и
и 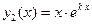 , а потому общее решение однородного уравнения (3) имеет вид:
, а потому общее решение однородного уравнения (3) имеет вид:
(10)  .
.
3. Характеристическое уравнение (5) не имеет действительных корней, что соответствует случаю 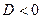 . Тогда в формуле (4)
. Тогда в формуле (4)  и
и 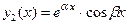 , а потому общее решение однородного уравнения (3) имеет вид:
, а потому общее решение однородного уравнения (3) имеет вид:
(11)  ,
,
где
(12)  ,
, 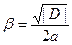 ,
,
а  ,
,  и
и 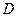 суть коэффициенты характеристического уравнения (5) и его дискриминант (6).
суть коэффициенты характеристического уравнения (5) и его дискриминант (6).
Доказательство. Как показано в теореме 1 предыдущего параграфа, функции 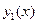 и
и 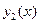 в формуле общего решения (4) должны удовлетворять двум условиям – быть линейно независимыми и быть решениями соответствующего однородного уравнения. Первое требование – независимость функций
в формуле общего решения (4) должны удовлетворять двум условиям – быть линейно независимыми и быть решениями соответствующего однородного уравнения. Первое требование – независимость функций 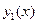 и
и 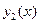 , фигурирующих в перечисленных трех случаях условия данной теоремы – доказывалась в примерах 1, 2 и 3 предыдущего параграфа. Поэтому осталось доказать, что в каждом из упомянутых трех случаев соответствующие функции
, фигурирующих в перечисленных трех случаях условия данной теоремы – доказывалась в примерах 1, 2 и 3 предыдущего параграфа. Поэтому осталось доказать, что в каждом из упомянутых трех случаев соответствующие функции 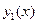 и
и 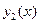 являются решениями однородного уравнения (3), т.е. при подстановке в него дают верные тождества. Докажем это, например, для первого случая, когда дискриминант характеристического уравнения
являются решениями однородного уравнения (3), т.е. при подстановке в него дают верные тождества. Докажем это, например, для первого случая, когда дискриминант характеристического уравнения  , а само это уравнение имеет два различных корня
, а само это уравнение имеет два различных корня  и
и 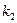 (в двух других случаях, когда
(в двух других случаях, когда 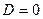 или
или 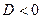 , доказательство проводится по той же схеме, хотя и с более громоздкими выкладками). Поскольку число
, доказательство проводится по той же схеме, хотя и с более громоздкими выкладками). Поскольку число  является корнем характеристического уравнения (5), то при подстановке в него вместо
является корнем характеристического уравнения (5), то при подстановке в него вместо  дает верное равенство:
дает верное равенство:
(13) 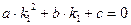 .
.
Вычислим предварительно производные от функции 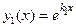 :
:
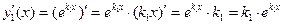 ,
, 
Подставим теперь функцию 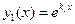 в левую часть дифференциального уравнения (3) с учетом только что вычисленных производных и убедимся, что получим 0 (т.е.
в левую часть дифференциального уравнения (3) с учетом только что вычисленных производных и убедимся, что получим 0 (т.е. 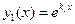 будет действительно решением этого уравнения):
будет действительно решением этого уравнения):
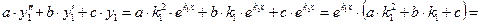 {из (13)}
{из (13)} 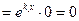 .
.
Аналогично доказывается, что и функция 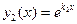 тоже является в этом случае решением дифференциального уравнения (3), что и требовалось показать.
тоже является в этом случае решением дифференциального уравнения (3), что и требовалось показать.
Решим несколько примеров на применение формул (9), (10) и (11).
Пример 1. Найти общее решение уравнения 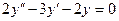 .
.
Решение. Это линейное однородное уравнение с постоянными коэффициентами вида (3). Построим характеристическое уравнение, заменяя в исходном уравнении 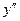 на
на 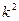 ,
,  на
на  , а
, а  на
на 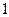 :
: 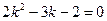 . Найдем дискриминант этого квадратного уравнения по формуле (6):
. Найдем дискриминант этого квадратного уравнения по формуле (6): 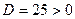 . Поэтому характеристическое уравнение имеет 2 различных корня, вычисляемых по формуле (7):
. Поэтому характеристическое уравнение имеет 2 различных корня, вычисляемых по формуле (7): 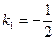 ,
, 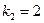 . Таким образом, мы находимся в рамках первого случая в условии теоремы 1 (корни
. Таким образом, мы находимся в рамках первого случая в условии теоремы 1 (корни  и
и 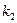 различны), а потому общее решение исходного уравнения получаем из формулы (9) с вычисленными значениями
различны), а потому общее решение исходного уравнения получаем из формулы (9) с вычисленными значениями 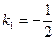 и
и 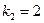 :
: 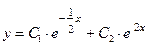 .
.
Пример 2. Найти решение задачи Коши 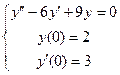 .
.
Решение. Найдем сначала общее решение уравнения  (объединяющее все решения этого уравнения), а потом выделим из него то, которое удовлетворяет предложенным начальным условиям:
(объединяющее все решения этого уравнения), а потом выделим из него то, которое удовлетворяет предложенным начальным условиям: 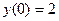 и
и 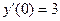 . Это опять линейное однородное уравнение с постоянными коэффициентами вида (3). Построим характеристическое уравнение, заменяя
. Это опять линейное однородное уравнение с постоянными коэффициентами вида (3). Построим характеристическое уравнение, заменяя 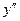 на
на 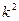 ,
,  на
на  , а
, а  на
на 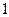 :
: 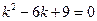 . Найдем дискриминант этого квадратного уравнения по формуле (6):
. Найдем дискриминант этого квадратного уравнения по формуле (6):  . Поэтому характеристическое уравнение имеет только один корень, который можно вычислить по формуле (8), получим:
. Поэтому характеристическое уравнение имеет только один корень, который можно вычислить по формуле (8), получим: 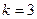 . Таким образом, мы находимся в рамках второго случая в условии теоремы 1 (характеристическое уравнение имеет только один корень
. Таким образом, мы находимся в рамках второго случая в условии теоремы 1 (характеристическое уравнение имеет только один корень 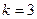 ), а потому общее решение исходного уравнения получаем из формулы (10) с подстановкой вы нее
), а потому общее решение исходного уравнения получаем из формулы (10) с подстановкой вы нее 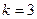 :
:
(14) 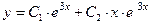 .
.
Для получения решения исходной задачи Коши осталось найти такие значения произвольных постоянных  и
и 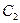 , при которых функция в (14) будет удовлетворять дополнительным условиям:
, при которых функция в (14) будет удовлетворять дополнительным условиям: 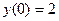 и
и  . Условие
. Условие 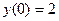 говорит о том, что при подстановке
говорит о том, что при подстановке  функция в (14) должна принимать значение
функция в (14) должна принимать значение  . Подставляя
. Подставляя  и
и  в (14), получаем, что для
в (14), получаем, что для  и
и 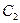 должно выполняться:
должно выполняться: 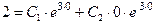 . Учитывая, что
. Учитывая, что  , получаем, что
, получаем, что 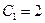 . Мы можем подставить найденное
. Мы можем подставить найденное 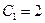 в (14) и получим, что нужное нам решение имеет вид:
в (14) и получим, что нужное нам решение имеет вид:
(15) 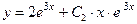 .
.
Осталось найти значение второй постоянной 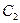 , воспользовавшись вторым дополнительным условием
, воспользовавшись вторым дополнительным условием  . Это условие говорит о том, что при подстановке
. Это условие говорит о том, что при подстановке  в выражение для производной функции в (15) должно получаться значение
в выражение для производной функции в (15) должно получаться значение 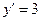 . Поскольку у нас пока нет выражения для производной функции (15) (а потому и некуда пока подставлять
. Поскольку у нас пока нет выражения для производной функции (15) (а потому и некуда пока подставлять  ), то получим это выражение по правилам вычисления производных:
), то получим это выражение по правилам вычисления производных: 


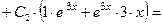
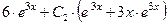 . Таким образом, выражение для производной имеет вид
. Таким образом, выражение для производной имеет вид
(16)  .
.
Теперь мы уже можем подставить в него  и требовать, чтобы при этом получалось значение
и требовать, чтобы при этом получалось значение 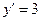 (в соответствии с условием
(в соответствии с условием  ). Подставляя в (16)
). Подставляя в (16)  и
и 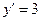 , получим следующее условие для определения
, получим следующее условие для определения 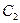 :
: 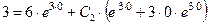 , т.е.
, т.е. 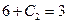 , откуда
, откуда 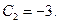 Подставляя это значение
Подставляя это значение 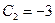 в (15), получаем окончательное выражение для функции, являющейся решением исходной задачи Коши:
в (15), получаем окончательное выражение для функции, являющейся решением исходной задачи Коши: 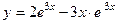 .
.
Пример 3. Найти общее решение уравнения 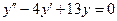 .
.
Решение. Это линейное однородное уравнение с постоянными коэффициентами вида (3) (т.е. вида 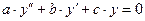 ) с параметрами:
) с параметрами:
(17)  ,
, 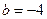 ,
, 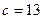 .
.
Построим характеристическое уравнение, заменяя в исходном уравнении 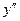 на
на 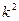 ,
,  на
на  , а
, а  на
на 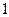 :
: 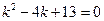 . Найдем дискриминант этого квадратного уравнения по формуле (6):
. Найдем дискриминант этого квадратного уравнения по формуле (6):  . Поэтому характеристическое уравнение не имеет действительных корней. Таким образом, мы находимся в рамках третьего случая в условии теоремы 1 (
. Поэтому характеристическое уравнение не имеет действительных корней. Таким образом, мы находимся в рамках третьего случая в условии теоремы 1 (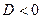 , корней нет), а потому общее решение исходного уравнения получаем из формулы (11), в которой параметры
, корней нет), а потому общее решение исходного уравнения получаем из формулы (11), в которой параметры 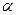 и
и  вычисляются по формулам (12) с учетом (17):
вычисляются по формулам (12) с учетом (17): 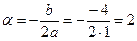 ,
, 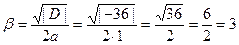 . Подставляя полученные значения
. Подставляя полученные значения  и
и 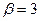 в (11), получаем выражение для общего решения исходного уравнения:
в (11), получаем выражение для общего решения исходного уравнения: 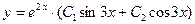 .
.
Теперь рассмотрим метод нахождения общего решения неоднородного линейного уравнения с постоянными коэффициентами (2). Как отмечено в Правиле 2 предыдущего параграфа, общее решение любого неоднородного линейного уравнения есть сумма общего решения соответствующего однородного уравнения и какого-либо частного решения самого неоднородного уравнения:
(18) 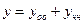 ,
,
где  есть общее решение однородного уравнения, а
есть общее решение однородного уравнения, а 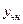 − частное решение неоднородного уравнения. Таким образом, общее решение неоднородного уравнения (2) вычисляется по формуле (18), где
− частное решение неоднородного уравнения. Таким образом, общее решение неоднородного уравнения (2) вычисляется по формуле (18), где  есть общее решение соответствующего однородного уравнения (3), а
есть общее решение соответствующего однородного уравнения (3), а 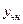 − какое-либо частное решение самого неоднородного уравнения (2). Выше мы уже подробно обсудили методы нахождения общего решения
− какое-либо частное решение самого неоднородного уравнения (2). Выше мы уже подробно обсудили методы нахождения общего решения  однородного уравнения (3) (см. формулу (4), в которой вид функций
однородного уравнения (3) (см. формулу (4), в которой вид функций 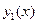 и
и 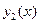 описан в теореме 1), а потому осталось научиться находить
описан в теореме 1), а потому осталось научиться находить 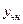 − какое-либо частное решение самого неоднородного уравнения (2).
− какое-либо частное решение самого неоднородного уравнения (2).
Мы обсудим здесь метод нахождения такого решения, известного под названием метод неопределенных коэффициентов. Недостатком этого метода является то, что он позволяет найти вид частного решения 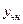 уравнения (2) не для любого вида правой части
уравнения (2) не для любого вида правой части 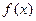 в этом уравнении. Но все-таки для многих важных случаев (они перечислены ниже в теореме 2) этот метод работает. Прежде, чем описывать суть этого метода, напомним, что многочленом степени
в этом уравнении. Но все-таки для многих важных случаев (они перечислены ниже в теореме 2) этот метод работает. Прежде, чем описывать суть этого метода, напомним, что многочленом степени 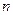 (будем обозначать его
(будем обозначать его 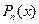 или
или  ) называется функция, представляющая собой сумму всех степеней (до
) называется функция, представляющая собой сумму всех степеней (до 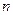 включительно) переменной
включительно) переменной  с некоторыми числовыми коэффициентами перед ними:
с некоторыми числовыми коэффициентами перед ними:
(19) 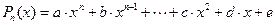 ,
,
где  − произвольные числа (коэффициенты многочлена). Например, общий вид многочлена 2-й степени:
− произвольные числа (коэффициенты многочлена). Например, общий вид многочлена 2-й степени:
(20) 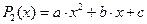 ,
,
а многочлена 1-й степени:
(21) 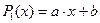 .
.
Многочленом нулевой степени ( называется любое число:
называется любое число:
(22) 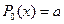 .
.
Метод неопределенных коэффициентов основан на следующей теореме (которую приводим без доказательства).
Теорема 2.
1. Пусть правая часть 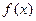 в неоднородном уравнении (2) имеет вид
в неоднородном уравнении (2) имеет вид
(23) 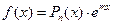 ,
,
где 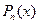 − некоторый многочлен некоторой степени n. Тогда у уравнения (2) обязательно имеется решение вида
− некоторый многочлен некоторой степени n. Тогда у уравнения (2) обязательно имеется решение вида
(24)  ,
,
где число  в показателе экспоненты то же самое, что в правой части (23),
в показателе экспоненты то же самое, что в правой части (23),  − многочлен степени
− многочлен степени 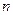 (той же степени, что и
(той же степени, что и 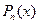 в (23), но, возможно, с какими-то уже другими коэффициентами), а показатель степени
в (23), но, возможно, с какими-то уже другими коэффициентами), а показатель степени  может принимать 3 значения:
может принимать 3 значения:
а) 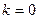 , если число
, если число  в (23) не является корнем характеристического уравнения (5) соответствующего однородного уравнения (3);
в (23) не является корнем характеристического уравнения (5) соответствующего однородного уравнения (3);
б) 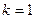 , если у этого характеристического уравнения имеется два различных корня, причем один из них равен числу
, если у этого характеристического уравнения имеется два различных корня, причем один из них равен числу  в (23), а другой нет;
в (23), а другой нет;
в)  , если характеристическое уравнение имеет только один корень (т.е. его дискриминант = 0) и именно равный числу
, если характеристическое уравнение имеет только один корень (т.е. его дискриминант = 0) и именно равный числу  в (23).
в (23).
2. Пусть правая часть 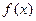 в неоднородном уравнении (2) имеет вид
в неоднородном уравнении (2) имеет вид
(25)  ,
,
где  ,
,  и
и  − некоторые числа. Тогда у уравнения (2) обязательно имеется решение вида
− некоторые числа. Тогда у уравнения (2) обязательно имеется решение вида
(26) 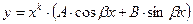 ,
,
где число  под синусом и косинусом то же самое, что в (25) (но числа
под синусом и косинусом то же самое, что в (25) (но числа 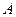 и
и  могут уже отличаться от
могут уже отличаться от  и
и  в (25)), а показатель степени
в (25)), а показатель степени  может принимать 2 значения:
может принимать 2 значения:
а) 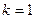 , если исходное уравнение (2) имеет вид
, если исходное уравнение (2) имеет вид
(27) 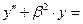
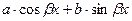
с некоторыми числами  ,
,  и
и  ;
;
б) 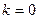 , если уравнение (2) отличается от вида (27).
, если уравнение (2) отличается от вида (27).
Замечание. Выделим отдельно один часто встречающийся случай теоремы 2. Речь идет о том случае, когда правая часть 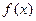 в уравнении (2) является многочленом:
в уравнении (2) является многочленом:
(28) 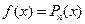 ,
,
где 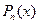 − некоторый многочлен некоторой степени n. Поскольку это соответствует случаю, когда
− некоторый многочлен некоторой степени n. Поскольку это соответствует случаю, когда 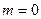 в (23) (так как тогда в (23):
в (23) (так как тогда в (23): 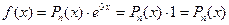 ), то из теоремы следует, что тогда у уравнения (2) обязательно имеется решение вида
), то из теоремы следует, что тогда у уравнения (2) обязательно имеется решение вида
(29)  ,
,
где  − многочлен степени
− многочлен степени 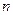 (той же степени, что и
(той же степени, что и 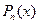 в (28), но, возможно, с какими-то другими коэффициентами), а показатель степени
в (28), но, возможно, с какими-то другими коэффициентами), а показатель степени  может принимать 3 значения:
может принимать 3 значения:
а) 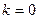 , если число
, если число  не является корнем характеристического уравнения (5) соответствующего однородного уравнения (3);
не является корнем характеристического уравнения (5) соответствующего однородного уравнения (3);
б) 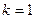 , если у этого характеристического уравнения имеется два различных корня, причем один из них равен 0, а другой нет;
, если у этого характеристического уравнения имеется два различных корня, причем один из них равен 0, а другой нет;
в)  , если характеристическое уравнение имеет только один корень, да и тот равен нулю.
, если характеристическое уравнение имеет только один корень, да и тот равен нулю.
Как сказано выше, на этой теореме базируется метод неопределенных коэффициентов нахождения частного решения 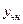 неоднородного уравнения (2). Согласно этому методу, для нахождения частного решения уравнения (2) необходимо:
неоднородного уравнения (2). Согласно этому методу, для нахождения частного решения уравнения (2) необходимо:
1. В зависимости от того, имеет ли правая часть 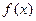 уравнения (2) вид (23) или (25) или (28), записать общий вид частного решения (24) или (26) или (29) с пока неопределенными (т.е. в буквах) коэффициентами многочлена
уравнения (2) вид (23) или (25) или (28), записать общий вид частного решения (24) или (26) или (29) с пока неопределенными (т.е. в буквах) коэффициентами многочлена  в (24) или (29) или неопределенными коэффициентами
в (24) или (29) или неопределенными коэффициентами 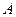 и
и  в (26).
в (26).
2. Найти конкретные значения указанных неопределенных коэффициентов из того условия, чтобы выписанная в первом пункте функция при этих значениях коэффициентов действительно оказывалась бы решением уравнения (2), т.е. при подстановке в него давала бы верное тождество.
3. Подставить полученные значения вместо неопределенных коэффициентов в записи частного решения, выписанного в первом пункте.
Практическое применение метода неопределенных коэффициентов разберем на примерах.
Пример 4. Найти общее решение уравнения
(30) 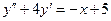 .
.
Решение. Это, очевидно, линейное неоднородное дифференциальное уравнение с постоянными коэффициентами вида (2). Согласно формуле (18), его общее решение имеет вид
(31) 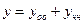 ,
,
где  есть общее решение соответствующего однородного уравнения
есть общее решение соответствующего однородного уравнения
(32) 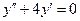 ,
,
а 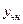 − частное решение самого неоднородного уравнения (30). Найдем вид каждого слагаемого
− частное решение самого неоднородного уравнения (30). Найдем вид каждого слагаемого  и
и 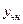 в (31). Уравнение (32) − это линейное однородное уравнение с постоянными коэффициентами вида (3). По правилу нахождения его общего решения (см. теорему 1) сначала строим его характеристическое уравнение, заменяя в уравнении (32)
в (31). Уравнение (32) − это линейное однородное уравнение с постоянными коэффициентами вида (3). По правилу нахождения его общего решения (см. теорему 1) сначала строим его характеристическое уравнение, заменяя в уравнении (32) 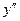 на
на 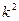 ,
,  на
на  , а
, а  на
на 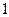 (правда
(правда  в это уравнение не входит, поэтому заменять его на
в это уравнение не входит, поэтому заменять его на 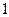 нет необходимости):
нет необходимости):  . Если в левой части характеристического уравнения вынести
. Если в левой части характеристического уравнения вынести  , то получим
, то получим 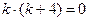 . Поэтому и без применения общих формул решения квадратного уравнения ясно, что это уравнение имеет 2 корня
. Поэтому и без применения общих формул решения квадратного уравнения ясно, что это уравнение имеет 2 корня 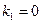 и
и 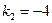 . Поскольку
. Поскольку 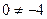 , то мы находимся в рамках первого случая в условии теоремы 1 (корни
, то мы находимся в рамках первого случая в условии теоремы 1 (корни  и
и 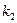 различны), а потому общее решение однородного уравнения (32) получаем из формулы (9) с вычисленными значениями
различны), а потому общее решение однородного уравнения (32) получаем из формулы (9) с вычисленными значениями 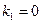 и
и 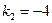 :
: 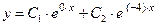 . Поскольку
. Поскольку 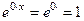 , то получаем окончательный вид общего решения однородного уравнения (32):
, то получаем окончательный вид общего решения однородного уравнения (32):
(33)  .
.
Итак, вид первого слагаемого  в формуле (31) установлен. Найдем теперь второе слагаемое
в формуле (31) установлен. Найдем теперь второе слагаемое 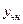 − частное решение самого неоднородного уравнения (30) по приведенной выше схеме метода неопределенных коэффициентов.
− частное решение самого неоднородного уравнения (30) по приведенной выше схеме метода неопределенных коэффициентов.
1. Поскольку правая часть этого уравнения 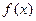
 есть многочлен первой степени (так как имеет вид (21)), то мы находимся в рамках случая (28) при
есть многочлен первой степени (так как имеет вид (21)), то мы находимся в рамках случая (28) при 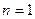 . Согласно этому случаю, частное решение
. Согласно этому случаю, частное решение 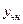 неоднородного уравнения (30) имеет вид (29) при
неоднородного уравнения (30) имеет вид (29) при 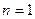 :
:
(34)  ,
,
где  − многочлен тоже первой степени, т.е. вида (21)
− многочлен тоже первой степени, т.е. вида (21)
(35) 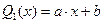
с неопределенными (пока) коэффициентами  и
и  . Поскольку один из корней характеристического многочлена (напомним, что эти корни были
. Поскольку один из корней характеристического многочлена (напомним, что эти корни были 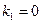 и
и 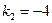 ) равен нулю, а другой нет, то показатель степени в (34)
) равен нулю, а другой нет, то показатель степени в (34) 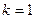 (это случай б) в замечании после формулы (29)). Учитывая это, а также (35), формулу для частного решения (34) можно записать в виде
(это случай б) в замечании после формулы (29)). Учитывая это, а также (35), формулу для частного решения (34) можно записать в виде  или (раскрывая скобки):
или (раскрывая скобки):
(36) 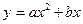 .
.
Итак, согласно теореме 2, у уравнения (30) имеется частное решение вида (36) с какими-то нам пока неизвестными коэффициентами – числами  и
и  .
.
2. Найдем конкретные значения указанных неопределенных коэффициентов  и
и  из того условия, чтобы при этих
из того условия, чтобы при этих  и
и  функция в (36) действительно оказалась бы решением уравнения (30), т.е. при подстановке в него давала бы верное тождество. Подставим функцию (36) в левую часть уравнения (30) и потребуем, чтобы при этом действительно получилась правая часть этого уравнения, т.е.
функция в (36) действительно оказалась бы решением уравнения (30), т.е. при подстановке в него давала бы верное тождество. Подставим функцию (36) в левую часть уравнения (30) и потребуем, чтобы при этом действительно получилась правая часть этого уравнения, т.е. 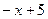 . Но в левой части (30) содержится не сама искомая функция, а ее производные
. Но в левой части (30) содержится не сама искомая функция, а ее производные  и
и 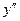 , а потому надо сначала вычислить выражения для производных
, а потому надо сначала вычислить выражения для производных  и
и 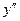 функции (36), а затем их подставлять в левую часть (30). Находим выражения для указанных производных, учитывая, что
функции (36), а затем их подставлять в левую часть (30). Находим выражения для указанных производных, учитывая, что  и
и  есть некоторые числа (хотя нам пока и неизвестные):
есть некоторые числа (хотя нам пока и неизвестные):  , т.е.
, т.е.
(37) 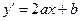 .
.
Найдем выражение для второй производной: 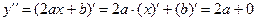 . Таким образом,
. Таким образом,
(38)  .
.
Подставим теперь выражения (37) и (38) для  и
и 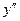 в левую часть уравнения (30) и потребуем выполнение тождества
в левую часть уравнения (30) и потребуем выполнение тождества 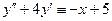 :
:  или
или 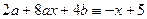 или
или
(39) 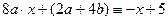 .
.
Какими же должны быть числа  и
и  , чтобы было справедливо тождество (39)? Поскольку справа при
, чтобы было справедливо тождество (39)? Поскольку справа при  стоит коэффициент
стоит коэффициент 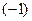 , а слева
, а слева 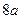 , то должно выполниться:
, то должно выполниться:  . Поскольку кроме этого справа стоит число
. Поскольку кроме этого справа стоит число  , а слева
, а слева 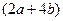 , то должно выполниться:
, то должно выполниться:  . Таким образом, для того, чтобы функция в (36) была решением уравнения (30), числа
. Таким образом, для того, чтобы функция в (36) была решением уравнения (30), числа  и
и  в (36) должны удовлетворять системе уравнений:
в (36) должны удовлетворять системе уравнений: 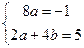 . Из первого уравнения системы сразу получим, что
. Из первого уравнения системы сразу получим, что 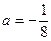 . Для нахождения числа
. Для нахождения числа  подставим
подставим 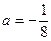 во второе уравнение системы:
во второе уравнение системы: 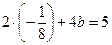 или
или  или
или 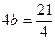 , откуда
, откуда 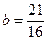 . Таким образом, функция в (36) является решением уравнения (30) при
. Таким образом, функция в (36) является решением уравнения (30) при 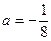 и
и 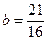 .
.
3. Подставляем полученные значения неопределенных коэффициентов 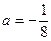 и
и 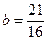 в (36) и получаем, что частное решение неоднородного уравнения имеет вид:
в (36) и получаем, что частное решение неоднородного уравнения имеет вид:
(40) 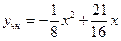 .
.
Подставляя теперь в (31) полученные выражения для  из (33) и
из (33) и 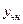 из (40), получаем окончательный вид общего решения исходного уравнения (30):
из (40), получаем окончательный вид общего решения исходного уравнения (30):
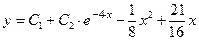 .
.
Пример 5. Найти общее решение уравнения
(41) 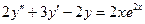 .
.
Решение. Это линейное неоднородное дифференциальное уравнение с постоянными коэффициентами вида (2), а потому по формуле (18) его общее решение имеет вид 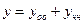 , где
, где  есть общее решение соответствующего однородного уравнения
есть общее решение соответствующего однородного уравнения
(42) 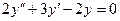 ,
,


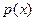 и
и  , стоящие множителями при
, стоящие множителями при  и
и 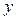 , являются постоянными, т.е. числами. Таким образом, линейными дифференциальными уравнениями второго порядка с постоянными коэффициентами называются уравнения вида
, являются постоянными, т.е. числами. Таким образом, линейными дифференциальными уравнениями второго порядка с постоянными коэффициентами называются уравнения вида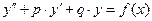 ,
,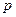 и
и 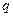 − произвольные числа, а
− произвольные числа, а 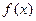 − непрерывная на некотором интервале
− непрерывная на некотором интервале  функция. Поскольку уравнение (1) является частным случаем общего линейного дифференциального уравнения 2-го порядка, то к нему применимы оба правила (Правило 1 и Правило 2) о структуре решений однородного и неоднородного уравнения, сформулированные в предыдущем параграфе.
функция. Поскольку уравнение (1) является частным случаем общего линейного дифференциального уравнения 2-го порядка, то к нему применимы оба правила (Правило 1 и Правило 2) о структуре решений однородного и неоднородного уравнения, сформулированные в предыдущем параграфе.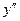 тоже стоит произвольный числовой коэффициент:
тоже стоит произвольный числовой коэффициент: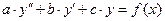 ,
, ,
, 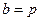 и
и 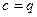 ). С другой стороны, если разделить обе части уравнения (2) на
). С другой стороны, если разделить обе части уравнения (2) на  , то коэффициент при
, то коэффициент при 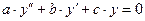 .
.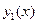 и
и 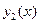 и выписать формулу для общего решения:
и выписать формулу для общего решения: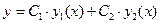 ,
, и
и 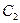 − произвольные постоянные.
− произвольные постоянные.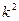 ,
,  , а
, а  на
на 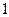 :
: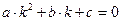 .
.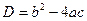 .
.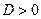 , то характеристическое уравнение (5) имеет два различных корня
, то характеристическое уравнение (5) имеет два различных корня  и
и 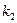 , вычисляемых по известным формулам корней квадратного уравнения:
, вычисляемых по известным формулам корней квадратного уравнения: .
.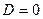 , то характеристическое уравнение имеет один корень
, то характеристическое уравнение имеет один корень 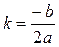 .
.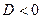 , то характеристическое уравнение (5) не имеет корней (в области действительных чисел). Вид линейно независимых решений
, то характеристическое уравнение (5) не имеет корней (в области действительных чисел). Вид линейно независимых решений 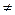
 в (6). Тогда в формуле (4)
в (6). Тогда в формуле (4) 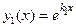 и
и 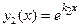 , а потому общее решение однородного уравнения (3) имеет вид:
, а потому общее решение однородного уравнения (3) имеет вид: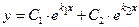 .
.
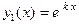 и
и 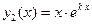 , а потому общее решение однородного уравнения (3) имеет вид:
, а потому общее решение однородного уравнения (3) имеет вид: .
. и
и 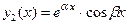 , а потому общее решение однородного уравнения (3) имеет вид:
, а потому общее решение однородного уравнения (3) имеет вид: ,
, ,
, 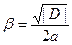 ,
, и
и 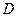 суть коэффициенты характеристического уравнения (5) и его дискриминант (6).
суть коэффициенты характеристического уравнения (5) и его дискриминант (6).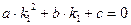 .
.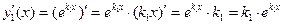 ,
, 
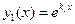 в левую часть дифференциального уравнения (3) с учетом только что вычисленных производных и убедимся, что получим 0 (т.е.
в левую часть дифференциального уравнения (3) с учетом только что вычисленных производных и убедимся, что получим 0 (т.е. 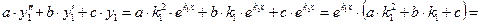 {из (13)}
{из (13)} 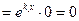 .
.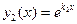 тоже является в этом случае решением дифференциального уравнения (3), что и требовалось показать.
тоже является в этом случае решением дифференциального уравнения (3), что и требовалось показать.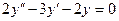 .
.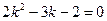 . Найдем дискриминант этого квадратного уравнения по формуле (6):
. Найдем дискриминант этого квадратного уравнения по формуле (6): 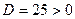 . Поэтому характеристическое уравнение имеет 2 различных корня, вычисляемых по формуле (7):
. Поэтому характеристическое уравнение имеет 2 различных корня, вычисляемых по формуле (7): 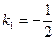 ,
, 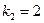 . Таким образом, мы находимся в рамках первого случая в условии теоремы 1 (корни
. Таким образом, мы находимся в рамках первого случая в условии теоремы 1 (корни 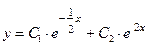 .
.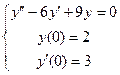 .
. (объединяющее все решения этого уравнения), а потом выделим из него то, которое удовлетворяет предложенным начальным условиям:
(объединяющее все решения этого уравнения), а потом выделим из него то, которое удовлетворяет предложенным начальным условиям: 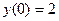 и
и 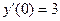 . Это опять линейное однородное уравнение с постоянными коэффициентами вида (3). Построим характеристическое уравнение, заменяя
. Это опять линейное однородное уравнение с постоянными коэффициентами вида (3). Построим характеристическое уравнение, заменяя 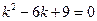 . Найдем дискриминант этого квадратного уравнения по формуле (6):
. Найдем дискриминант этого квадратного уравнения по формуле (6):  . Поэтому характеристическое уравнение имеет только один корень, который можно вычислить по формуле (8), получим:
. Поэтому характеристическое уравнение имеет только один корень, который можно вычислить по формуле (8), получим: 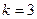 . Таким образом, мы находимся в рамках второго случая в условии теоремы 1 (характеристическое уравнение имеет только один корень
. Таким образом, мы находимся в рамках второго случая в условии теоремы 1 (характеристическое уравнение имеет только один корень 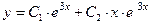 .
. . Условие
. Условие  функция в (14) должна принимать значение
функция в (14) должна принимать значение  . Подставляя
. Подставляя 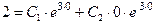 . Учитывая, что
. Учитывая, что  , получаем, что
, получаем, что 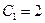 . Мы можем подставить найденное
. Мы можем подставить найденное 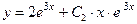 .
.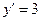 . Поскольку у нас пока нет выражения для производной функции (15) (а потому и некуда пока подставлять
. Поскольку у нас пока нет выражения для производной функции (15) (а потому и некуда пока подставлять 


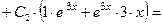
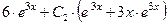 . Таким образом, выражение для производной имеет вид
. Таким образом, выражение для производной имеет вид .
.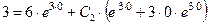 , т.е.
, т.е. 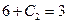 , откуда
, откуда 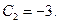 Подставляя это значение
Подставляя это значение 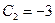 в (15), получаем окончательное выражение для функции, являющейся решением исходной задачи Коши:
в (15), получаем окончательное выражение для функции, являющейся решением исходной задачи Коши: 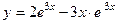 .
.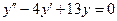 .
. ,
, 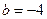 ,
, 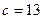 .
.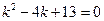 . Найдем дискриминант этого квадратного уравнения по формуле (6):
. Найдем дискриминант этого квадратного уравнения по формуле (6):  . Поэтому характеристическое уравнение не имеет действительных корней. Таким образом, мы находимся в рамках третьего случая в условии теоремы 1 (
. Поэтому характеристическое уравнение не имеет действительных корней. Таким образом, мы находимся в рамках третьего случая в условии теоремы 1 (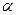 и
и  вычисляются по формулам (12) с учетом (17):
вычисляются по формулам (12) с учетом (17): 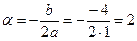 ,
, 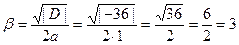 . Подставляя полученные значения
. Подставляя полученные значения  и
и 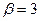 в (11), получаем выражение для общего решения исходного уравнения:
в (11), получаем выражение для общего решения исходного уравнения: 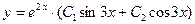 .
. ,
, есть общее решение однородного уравнения, а
есть общее решение однородного уравнения, а 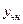 − частное решение неоднородного уравнения. Таким образом, общее решение неоднородного уравнения (2) вычисляется по формуле (18), где
− частное решение неоднородного уравнения. Таким образом, общее решение неоднородного уравнения (2) вычисляется по формуле (18), где 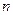 (будем обозначать его
(будем обозначать его 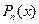 или
или  ) называется функция, представляющая собой сумму всех степеней (до
) называется функция, представляющая собой сумму всех степеней (до  с некоторыми числовыми коэффициентами перед ними:
с некоторыми числовыми коэффициентами перед ними: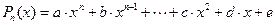 ,
, − произвольные числа (коэффициенты многочлена). Например, общий вид многочлена 2-й степени:
− произвольные числа (коэффициенты многочлена). Например, общий вид многочлена 2-й степени: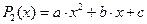 ,
,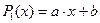 .
. называется любое число:
называется любое число: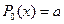 .
.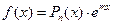 ,
,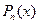 − некоторый многочлен некоторой степени n. Тогда у уравнения (2) обязательно имеется решение вида
− некоторый многочлен некоторой степени n. Тогда у уравнения (2) обязательно имеется решение вида ,
, в показателе экспоненты то же самое, что в правой части (23),
в показателе экспоненты то же самое, что в правой части (23),  , если число
, если число  , если у этого характеристического уравнения имеется два различных корня, причем один из них равен числу
, если у этого характеристического уравнения имеется два различных корня, причем один из них равен числу  , если характеристическое уравнение имеет только один корень (т.е. его дискриминант = 0) и именно равный числу
, если характеристическое уравнение имеет только один корень (т.е. его дискриминант = 0) и именно равный числу  ,
,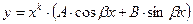 ,
,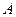 и
и  могут уже отличаться от
могут уже отличаться от 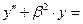
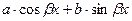
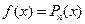 ,
,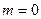 в (23) (так как тогда в (23):
в (23) (так как тогда в (23): 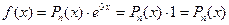 ), то из теоремы следует, что тогда у уравнения (2) обязательно имеется решение вида
), то из теоремы следует, что тогда у уравнения (2) обязательно имеется решение вида ,
, не является корнем характеристического уравнения (5) соответствующего однородного уравнения (3);
не является корнем характеристического уравнения (5) соответствующего однородного уравнения (3);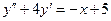 .
.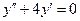 ,
, . Если в левой части характеристического уравнения вынести
. Если в левой части характеристического уравнения вынести 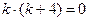 . Поэтому и без применения общих формул решения квадратного уравнения ясно, что это уравнение имеет 2 корня
. Поэтому и без применения общих формул решения квадратного уравнения ясно, что это уравнение имеет 2 корня 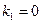 и
и 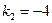 . Поскольку
. Поскольку 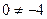 , то мы находимся в рамках первого случая в условии теоремы 1 (корни
, то мы находимся в рамках первого случая в условии теоремы 1 (корни 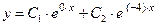 . Поскольку
. Поскольку 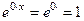 , то получаем окончательный вид общего решения однородного уравнения (32):
, то получаем окончательный вид общего решения однородного уравнения (32): .
. есть многочлен первой степени (так как имеет вид (21)), то мы находимся в рамках случая (28) при
есть многочлен первой степени (так как имеет вид (21)), то мы находимся в рамках случая (28) при 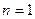 . Согласно этому случаю, частное решение
. Согласно этому случаю, частное решение  ,
, − многочлен тоже первой степени, т.е. вида (21)
− многочлен тоже первой степени, т.е. вида (21)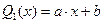
 или (раскрывая скобки):
или (раскрывая скобки):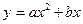 .
.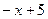 . Но в левой части (30) содержится не сама искомая функция, а ее производные
. Но в левой части (30) содержится не сама искомая функция, а ее производные  , т.е.
, т.е.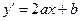 .
.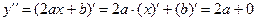 . Таким образом,
. Таким образом, .
.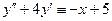 :
:  или
или 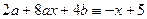 или
или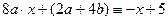 .
.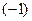 , а слева
, а слева 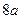 , то должно выполниться:
, то должно выполниться:  . Поскольку кроме этого справа стоит число
. Поскольку кроме этого справа стоит число  , а слева
, а слева 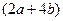 , то должно выполниться:
, то должно выполниться:  . Таким образом, для того, чтобы функция в (36) была решением уравнения (30), числа
. Таким образом, для того, чтобы функция в (36) была решением уравнения (30), числа 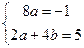 . Из первого уравнения системы сразу получим, что
. Из первого уравнения системы сразу получим, что 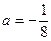 . Для нахождения числа
. Для нахождения числа 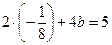 или
или  или
или 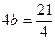 , откуда
, откуда 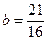 . Таким образом, функция в (36) является решением уравнения (30) при
. Таким образом, функция в (36) является решением уравнения (30) при 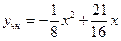 .
.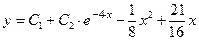 .
.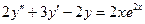 .
.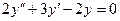 ,
,


