График функции  лучше всего характеризует характер зависимости некоторого фактора
лучше всего характеризует характер зависимости некоторого фактора  от другого фактора
от другого фактора  , задаваемой этой функцией. На графике сразу видно, где функция возрастает, а где убывает и насколько быстро, сразу видны ее экстремумы, интервалы положительности и отрицательности ее значений и т.д.. Чего не скажешь, глядя на саму формулу
, задаваемой этой функцией. На графике сразу видно, где функция возрастает, а где убывает и насколько быстро, сразу видны ее экстремумы, интервалы положительности и отрицательности ее значений и т.д.. Чего не скажешь, глядя на саму формулу  , которой задается функция. Поэтому конечной целью исследования функции обычно является построение ее графика. Исследование функции на монотонность и экстремум (пройденное выше) значительно облегчает построение графика функции и в дальнейшем войдет в общую схему исследования функции и построения ее графика. Однако есть еще некоторые инструменты исследования
, которой задается функция. Поэтому конечной целью исследования функции обычно является построение ее графика. Исследование функции на монотонность и экстремум (пройденное выше) значительно облегчает построение графика функции и в дальнейшем войдет в общую схему исследования функции и построения ее графика. Однако есть еще некоторые инструменты исследования 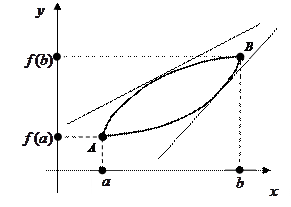 функции, помогающие достаточно точно строить ее график. Рассмотрим некоторую функцию
функции, помогающие достаточно точно строить ее график. Рассмотрим некоторую функцию  . Допустим, что мы при исследовании ее на монотонность установили, что на некотором интервале
. Допустим, что мы при исследовании ее на монотонность установили, что на некотором интервале  функция возрастает. Это означает, что при рисовании графика должны вести его строго вверх между точками А и В (с координатами
функция возрастает. Это означает, что при рисовании графика должны вести его строго вверх между точками А и В (с координатами  и
и  ). Но сделать это можно по-разному (см. рисунок): либо провести график выпуклостью вверх или вниз. Как же определить направление выпуклости. Первая производная (которая указала нам просто на возрастание функции) ответа уже не даст. В данном случае ответ даст уже вторая производная. Сначала заметим (по рисунку), что если кривая имеет выпуклость вверх, то она расположена под касательной, проведенной к любой из ее точек. А если выпуклость направлена вниз, то над касательной. Поэтому примем такие определения. Будем говорить, что график функции
). Но сделать это можно по-разному (см. рисунок): либо провести график выпуклостью вверх или вниз. Как же определить направление выпуклости. Первая производная (которая указала нам просто на возрастание функции) ответа уже не даст. В данном случае ответ даст уже вторая производная. Сначала заметим (по рисунку), что если кривая имеет выпуклость вверх, то она расположена под касательной, проведенной к любой из ее точек. А если выпуклость направлена вниз, то над касательной. Поэтому примем такие определения. Будем говорить, что график функции  имеет на интервале
имеет на интервале  выпуклость, направленную вверх (вниз), если он расположен
выпуклость, направленную вверх (вниз), если он расположен 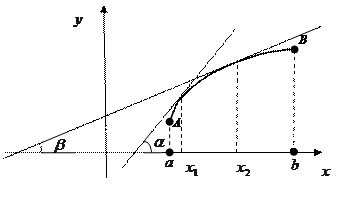 ниже (выше) любой касательной к графику функции на
ниже (выше) любой касательной к графику функции на  . Обозначается выпуклость вверх (вниз) на интервале
. Обозначается выпуклость вверх (вниз) на интервале  так:
так: 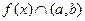
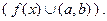 Каким же образом вторая производная покажет направление выпуклости графика? Обратимся к рисунку, на котором график функции
Каким же образом вторая производная покажет направление выпуклости графика? Обратимся к рисунку, на котором график функции  имеет на интервале
имеет на интервале  выпуклость вверх. Возьмем произвольные точки
выпуклость вверх. Возьмем произвольные точки  и
и  из
из  такие, что
такие, что 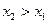 . Построим касательные в соответствующих точках графика (на рисунке). Пусть касательная в точке графика с координатой
. Построим касательные в соответствующих точках графика (на рисунке). Пусть касательная в точке графика с координатой  образует с осью
образует с осью  угол
угол  , а касательная с координатой
, а касательная с координатой  угол
угол 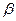 . Из геометрического смысла производной ясно, что
. Из геометрического смысла производной ясно, что 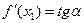 , а
, а 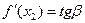 . Из рисунка видно, что при выпуклости графика вверх угол
. Из рисунка видно, что при выпуклости графика вверх угол 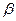 меньше угла
меньше угла  , а потому и
, а потому и 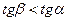 , т.е.
, т.е. 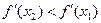 . Таким образом, выяснено, что большему значению х соответствует меньшее значение функции
. Таким образом, выяснено, что большему значению х соответствует меньшее значение функции  . Это (по определению) означает, что функция
. Это (по определению) означает, что функция  убывает на интервале
убывает на интервале  . Тогда по пройденному признаку убывания функции ее производная (т.е.
. Тогда по пройденному признаку убывания функции ее производная (т.е. 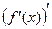 ) должна быть отрицательной на этом интервале. Но по определению производная от производной и есть вторая производная:
) должна быть отрицательной на этом интервале. Но по определению производная от производной и есть вторая производная:
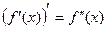 . Итак, мы доказали (точнее, показали), что если график функции имеет на некотором интервале выпуклость вверх, то вторая производная этой функции (если она, конечно, существует) является отрицательной (точнее, неположительной). Аналогично можно доказать-показать, что если график функции имеет на некотором интервале выпуклость вниз, то его вторая производная положительна (точнее, неотрицательна). Итак, справедлива
. Итак, мы доказали (точнее, показали), что если график функции имеет на некотором интервале выпуклость вверх, то вторая производная этой функции (если она, конечно, существует) является отрицательной (точнее, неположительной). Аналогично можно доказать-показать, что если график функции имеет на некотором интервале выпуклость вниз, то его вторая производная положительна (точнее, неотрицательна). Итак, справедлива
Теорема. Пусть у функции  существует на
существует на  вторая производная
вторая производная  . Тогда если
. Тогда если 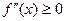 (
(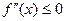 )на
)на  , то график функции имеет на этом интервале выпуклость вниз (вверх).
, то график функции имеет на этом интервале выпуклость вниз (вверх).
Таким образом, мы выяснили, что направление выпуклости графика функции определяется знаком ее второй производной.
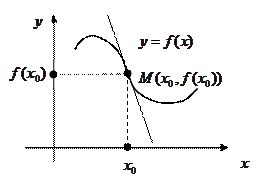 Прейдем теперь к так называемым точкам перегиба графика. Ранее точки экстремума (максимумы и минимумы) обычно разделяли участки монотонности функции разного вида (возрастание − убывание, убывание − возрастание). Аналогично, участки графика, имеющие разное направление выпуклости, тоже обычно разделяются некоторой характерной точкой графика, которая называется точкой перегиба (см. рисунок). Дадим определение такой точки. Точка
Прейдем теперь к так называемым точкам перегиба графика. Ранее точки экстремума (максимумы и минимумы) обычно разделяли участки монотонности функции разного вида (возрастание − убывание, убывание − возрастание). Аналогично, участки графика, имеющие разное направление выпуклости, тоже обычно разделяются некоторой характерной точкой графика, которая называется точкой перегиба (см. рисунок). Дадим определение такой точки. Точка  графика функции
графика функции  называется точкой перегиба, если выполнены условия:
называется точкой перегиба, если выполнены условия:
а) существует касательная к графику в этой точке;
б) по разные стороны от этой точки график имеет разные направления выпуклости.
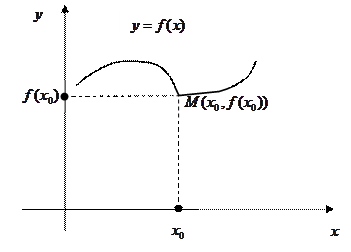 Требование существования касательной в точке перегиба продиктовано тем, что в точке перегиба переход от одного направления выпуклости к другому должен проходить «гладко» (перегиб, а не перелом). Отсутствие касательной, как было сказано раньше, ведет к появлению точки излома графика. Такая точка не считается точкой перегиба, даже если она действительно разделяет разные направления выпуклости графика (такова точка
Требование существования касательной в точке перегиба продиктовано тем, что в точке перегиба переход от одного направления выпуклости к другому должен проходить «гладко» (перегиб, а не перелом). Отсутствие касательной, как было сказано раньше, ведет к появлению точки излома графика. Такая точка не считается точкой перегиба, даже если она действительно разделяет разные направления выпуклости графика (такова точка  на рисунке слева). Если в точках экстремума (первая) производная функции (если она существует) обращается в 0, то в точках перегиба должна обращаться в 0 вторая производная функции (если она тоже существует). Это выражает следующая
на рисунке слева). Если в точках экстремума (первая) производная функции (если она существует) обращается в 0, то в точках перегиба должна обращаться в 0 вторая производная функции (если она тоже существует). Это выражает следующая
Теорема (необходимое условие точки перегиба). Пусть в точке  существует и непрерывна вторая производная функции
существует и непрерывна вторая производная функции 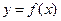 и
и  − точка перегиба ее графика. Тогда
− точка перегиба ее графика. Тогда 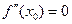 .
.
Таким образом, абсциссы (т.е.  -координаты) точек перегиба надо искать среди точек, в которых вторая производная обращается в 0 или не существует. Фактически это критические точки для первой производной. Дадим название таким точкам. Точки, в которых вторая производная функции
-координаты) точек перегиба надо искать среди точек, в которых вторая производная обращается в 0 или не существует. Фактически это критические точки для первой производной. Дадим название таким точкам. Точки, в которых вторая производная функции 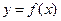 обращается в ноль или не существует, называются критическими точками функции второго рода. Вывод:
обращается в ноль или не существует, называются критическими точками функции второго рода. Вывод:  -координаты точек перегиба находятся только среди критических точек 2 рода. Однако не все такие точки (т.е критические точки 2 рода) обязательно соответствуют точкам перегиба. В качестве примера рассмотрим функцию
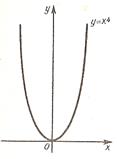
-координаты точек перегиба находятся только среди критических точек 2 рода. Однако не все такие точки (т.е критические точки 2 рода) обязательно соответствуют точкам перегиба. В качестве примера рассмотрим функцию 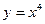 . Ее график имеет ту же форму, что и парабола
. Ее график имеет ту же форму, что и парабола  , но ветви у него круче идут вверх (см. рисунок). Точек перегиба у него нет, так как ее график имеет выпуклость вниз на всей числовой прямой (ее вторая производная равна
, но ветви у него круче идут вверх (см. рисунок). Точек перегиба у него нет, так как ее график имеет выпуклость вниз на всей числовой прямой (ее вторая производная равна 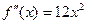 , а потому везде положительна). Однако ясно, что вторая производная обращается в 0 при
, а потому везде положительна). Однако ясно, что вторая производная обращается в 0 при  , а потому
, а потому  есть критическая точка 2 рода. Но соответствующая ей точка графика − начало координат
есть критическая точка 2 рода. Но соответствующая ей точка графика − начало координат 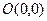 − не точка перегиба. Поэтому для исследования произвольных функций опять нужен алгоритм, позволяющий отсеивать критические точки функции 2 рода, не дающие перегиб. Такой алгоритм прост и нагляден.
− не точка перегиба. Поэтому для исследования произвольных функций опять нужен алгоритм, позволяющий отсеивать критические точки функции 2 рода, не дающие перегиб. Такой алгоритм прост и нагляден.
 Теорема (достаточное условие точки перегиба). Пусть функция
Теорема (достаточное условие точки перегиба). Пусть функция  имеет вторую производную
имеет вторую производную  в некоторой окрестности точки
в некоторой окрестности точки  . Тогда если в пределах указанной окрестности эта производная имеет разные знаки слева и справа от точки
. Тогда если в пределах указанной окрестности эта производная имеет разные знаки слева и справа от точки  , то график функции имеет перегиб в точке
, то график функции имеет перегиб в точке  .
.
Доказательство очевидно, так как разные знаки второй производной означают разное направление выпуклости справа и слева от  .
.
Замечание. Теорема остается верной и при более слабых условиях. Условие существования второй производной в окрестности точки  (включая ее саму) можно заменить наличием второй производной в выколотой окрестности этой точки (т.е. без самой точки
(включая ее саму) можно заменить наличием второй производной в выколотой окрестности этой точки (т.е. без самой точки  ) и наличием касательной к графику в точке
) и наличием касательной к графику в точке  (т.е. существованием производной
(т.е. существованием производной  в самой точке
в самой точке  ).
).
Итак, вопрос о направлении выпуклости и точках перегиба решается с помощью второй производной.
Пример 1. Исследовать график функции 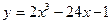 на выпуклость и точки перегиба.
на выпуклость и точки перегиба.
Решение. Мы уже ранее исследовали эту функцию на монотонность и экстремумы. Ищем критические точки 2 рода. Находим первую и вторую производную: 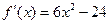 ,
, 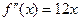 . Вторая производная существует на всей числовой прямой и обращается в 0 только при
. Вторая производная существует на всей числовой прямой и обращается в 0 только при  (критическая точка функции 2 рода), причем
(критическая точка функции 2 рода), причем 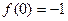 . Поэтому
. Поэтому 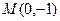 − единственная точка графика функции, подозрительная на точку перегиба этого графика. По аналогии с исследованием
− единственная точка графика функции, подозрительная на точку перегиба этого графика. По аналогии с исследованием 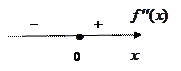 функции на монотонность и экстремумы наносим точку
функции на монотонность и экстремумы наносим точку  на числовую прямую и исследуем знаки второй производной на получившихся интервалах. Очевидно, что
на числовую прямую и исследуем знаки второй производной на получившихся интервалах. Очевидно, что 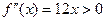 при
при 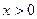 и
и 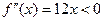 при
при 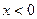 . Поэтому
. Поэтому 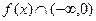 и
и 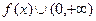 . Точка
. Точка  разделяет интервалы разных знаков для второй производной, а сама она в этой точке обращается в 0. Поэтому по теореме о достаточном условии точки перегиба критическая точка графика
разделяет интервалы разных знаков для второй производной, а сама она в этой точке обращается в 0. Поэтому по теореме о достаточном условии точки перегиба критическая точка графика 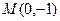 является точкой перегиба.
является точкой перегиба.
 Пример 2. Исследовать график функции
Пример 2. Исследовать график функции 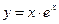 на выпуклость и точки перегиба.
на выпуклость и точки перегиба.
Решение. Ищем критические точки 2 рода. Находим производную (чтобы найти потом вторую производную): 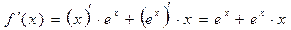 . Тогда вторая производная:
. Тогда вторая производная: 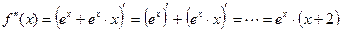 . Она существует на всей числовой прямой и обращается в 0 только при
. Она существует на всей числовой прямой и обращается в 0 только при  (так как функция
(так как функция 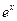 не обращается в 0 ни при каких значениях
не обращается в 0 ни при каких значениях  , оставаясь все время положительной). Итак,
, оставаясь все время положительной). Итак,  − единственная критическая точка функции 2 рода, причем
− единственная критическая точка функции 2 рода, причем 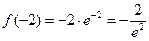 . Поэтому
. Поэтому 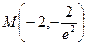 − единственная точка графика функции, подозрительная на точку перегиба. Наносим точку
− единственная точка графика функции, подозрительная на точку перегиба. Наносим точку  на числовую прямую и исследуем знаки второй производной
на числовую прямую и исследуем знаки второй производной 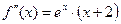 на получившихся интервалах. Поскольку экспонента
на получившихся интервалах. Поскольку экспонента 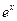 положительна при любых
положительна при любых  , то очевидно, что
, то очевидно, что 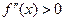 при
при 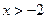 и
и 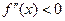 при
при 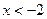 . Поэтому
. Поэтому 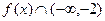 и
и 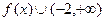 . Точка
. Точка  разделяет интервалы разных знаков для второй производной. Поэтому по теореме о достаточном условии точки перегиба точка графика
разделяет интервалы разных знаков для второй производной. Поэтому по теореме о достаточном условии точки перегиба точка графика 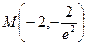 действительно является точкой перегиба.
действительно является точкой перегиба.
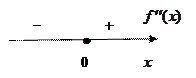 Пример 3. Провести аналогичное исследование для функции
Пример 3. Провести аналогичное исследование для функции 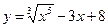 . Решение. Ищем критические точки 2 рода. Первая производная:
. Решение. Ищем критические точки 2 рода. Первая производная: 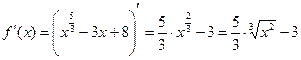 . Тогда вторая производная:
. Тогда вторая производная: 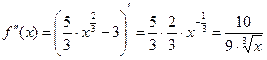 . Она не существует только при
. Она не существует только при  (на ноль делить нельзя), а потому
(на ноль делить нельзя), а потому  является критической точкой 2 рода. Других критических точек нет, поскольку
является критической точкой 2 рода. Других критических точек нет, поскольку 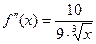 ни при каких значениях
ни при каких значениях  не обращается в 0 (дробь может обратиться в 0 только если ее числитель равен 0, а у нас в числителе стоит число 10, которое ни при каких
не обращается в 0 (дробь может обратиться в 0 только если ее числитель равен 0, а у нас в числителе стоит число 10, которое ни при каких  другим не станет). Итак,
другим не станет). Итак,  − единственная критическая точка функции 2 рода, причем
− единственная критическая точка функции 2 рода, причем 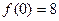 . Поэтому
. Поэтому 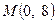 − единственная точка графика функции, подозрительная на точку перегиба. Наносим точку
− единственная точка графика функции, подозрительная на точку перегиба. Наносим точку  на числовую прямую и исследуем знаки второй производной
на числовую прямую и исследуем знаки второй производной 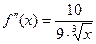 на получившихся интервалах. Из приведенного выражения для второй производной очевидно, что
на получившихся интервалах. Из приведенного выражения для второй производной очевидно, что 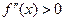 при
при 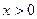 и
и 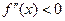 при
при 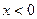 . Поэтому
. Поэтому 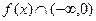 и
и 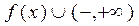 . Точка
. Точка  разделяет интервалы разных знаков для второй производной, но вторая производная
разделяет интервалы разных знаков для второй производной, но вторая производная 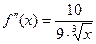 не существует при
не существует при  . Однако она существует в любой выколотой окрестности этой точки, а в самой точке
. Однако она существует в любой выколотой окрестности этой точки, а в самой точке  существует первая производная
существует первая производная 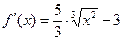 . Поэтому по замечанию к теореме о достаточном условии точки перегиба точка графика
. Поэтому по замечанию к теореме о достаточном условии точки перегиба точка графика  является точкой перегиба.
является точкой перегиба.
Асимптоты графика функции
Мы продолжаем изучать инструменты построения графика функции как наиболее удобного представления характера зависимости одной переменной от другой. При исследовании поведения функции на бесконечности (т.е. при  и
и  ) или вблизи точек разрыва второго рода часто оказывается, что график функции сколь угодно близко приближается к некоторым характерным прямым. Такие прямые называются асимптотами графика функции. Понятно, что если бы мы научились находить такие прямые, то это нам очень бы помогло для более точного построения графика. Прямые на координатной плоскости могут быть вертикальными (параллельными оси у) и наклонными (в частности, горизонтальными). В зависимости от того, к какой из них приближается график функции, будем различать вертикальные и наклонные асимптоты.
) или вблизи точек разрыва второго рода часто оказывается, что график функции сколь угодно близко приближается к некоторым характерным прямым. Такие прямые называются асимптотами графика функции. Понятно, что если бы мы научились находить такие прямые, то это нам очень бы помогло для более точного построения графика. Прямые на координатной плоскости могут быть вертикальными (параллельными оси у) и наклонными (в частности, горизонтальными). В зависимости от того, к какой из них приближается график функции, будем различать вертикальные и наклонные асимптоты.
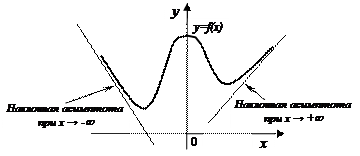 Изучим сначала наклонные асимптоты. Как видно из рисунка, график функции может приближаться к различным прямым при
Изучим сначала наклонные асимптоты. Как видно из рисунка, график функции может приближаться к различным прямым при  и
и  . Поэтому различают наклонные асимптоты при
. Поэтому различают наклонные асимптоты при  и наклонные асимптоты при
и наклонные асимптоты при  . Исходя из геометрических представлений, дадим определение наклонной асимптоты при
. Исходя из геометрических представлений, дадим определение наклонной асимптоты при  . Любая наклонная прямая имеет, как известно, уравнение вида
. Любая наклонная прямая имеет, как известно, уравнение вида 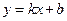 . Меняя числа
. Меняя числа  и
и  , получим уравнения всех наклонных прямых. При некоторой паре чисел
, получим уравнения всех наклонных прямых. При некоторой паре чисел  и
и  может получиться интересующая нас асимптота при
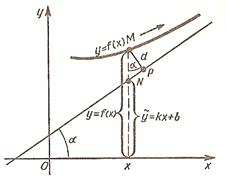
может получиться интересующая нас асимптота при  . Если мы найдем формулы для нахождения этих чисел, то научимся находить уравнение асимптоты, по которому сможем построить и саму асимптоту. Прежде всего нужно дать строгое определение асимптоты. Пока мы просто высказали желание уметь находить прямые, к которым «бесконечно близко примыкает график функции при удалении точки графика в бесконечность». Но фраза, заключенная в кавычках, ни коим образом не может являться строгим математическим определением, с которым можно «работать» математическими средствами. Поэтому попробуем дать строгое определение асимптоты, исходя из того, какое свойство графика мы хотим описать этим понятием. Итак, пусть прямая с уравнением
. Если мы найдем формулы для нахождения этих чисел, то научимся находить уравнение асимптоты, по которому сможем построить и саму асимптоту. Прежде всего нужно дать строгое определение асимптоты. Пока мы просто высказали желание уметь находить прямые, к которым «бесконечно близко примыкает график функции при удалении точки графика в бесконечность». Но фраза, заключенная в кавычках, ни коим образом не может являться строгим математическим определением, с которым можно «работать» математическими средствами. Поэтому попробуем дать строгое определение асимптоты, исходя из того, какое свойство графика мы хотим описать этим понятием. Итак, пусть прямая с уравнением 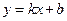 является наклонной асимптотой графика функции
является наклонной асимптотой графика функции  при
при  , т.е. к ней «бесконечно близко примыкает график функции при удалении точки графика в бесконечность» (см. рисунок). Пусть
, т.е. к ней «бесконечно близко примыкает график функции при удалении точки графика в бесконечность» (см. рисунок). Пусть  − текущая точка на оси
− текущая точка на оси  (мы потом устремим
(мы потом устремим  ). Длина отрезка
). Длина отрезка 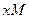 есть не что иное, как значение функции в точке
есть не что иное, как значение функции в точке  , т.е.
, т.е. 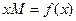 . Поскольку точка
. Поскольку точка  лежит на асимптоте с уравнением
лежит на асимптоте с уравнением 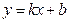 , то длина отрезка
, то длина отрезка 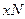 есть значение функции
есть значение функции 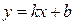 в текущей точке
в текущей точке  , т.е.
, т.е. 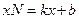 . Поэтому длина отрезка
. Поэтому длина отрезка 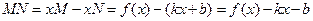 . По рисунку расстояние от точки
. По рисунку расстояние от точки 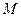 графика до асимптоты (которое и должно по нашему мнению стремиться к 0 при
графика до асимптоты (которое и должно по нашему мнению стремиться к 0 при  ):
): 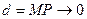 при
при  . Из прямоугольного треугольника
. Из прямоугольного треугольника 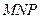 находим
находим 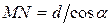 . Поэтому
. Поэтому 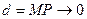 при
при  только в том случае, когда
только в том случае, когда 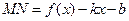 стремится к 0 при
стремится к 0 при  . Исходя из этого, можно принять следующее определение.
. Исходя из этого, можно принять следующее определение.  Наклонная прямая с уравнением
Наклонная прямая с уравнением 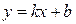 называется наклонной асимптотой графика функции
называется наклонной асимптотой графика функции  при
при  , если
, если
(1) 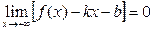 .
.
Вот это уже вполне математически корректное определение. Аналогично определяется наклонная асимптота при  : прямая с уравнением
: прямая с уравнением 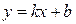 называется наклонной асимптотой графика функции
называется наклонной асимптотой графика функции  при
при  , если
, если
(2) 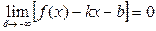 .
.
 Теперь, после введения строгого определения, вернемся к вопросу о нахождении формул для чисел
Теперь, после введения строгого определения, вернемся к вопросу о нахождении формул для чисел  и
и  в уравнении асимптоты
в уравнении асимптоты 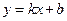 . Справедлива следующая
. Справедлива следующая
Теорема. Для того, чтобы график функции  имел наклонную асимптоту при
имел наклонную асимптоту при  с уравнением
с уравнением 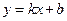 необходимо и достаточно, чтобы существовали два предела:
необходимо и достаточно, чтобы существовали два предела: 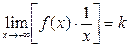 ,
, 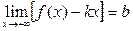 .
.
Докажем, например, необходимость. Пусть прямая 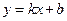 является асимптотой графика функции
является асимптотой графика функции  при
при  . Требуется доказать, что
. Требуется доказать, что 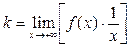 ,
, 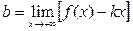 . Поскольку прямая
. Поскольку прямая 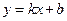 является асимптотой графика функции
является асимптотой графика функции  при
при  , то по определению (1) выполняется:
, то по определению (1) выполняется: 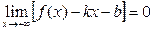 . Преобразуем:
. Преобразуем: 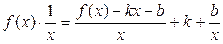 (приводя правую часть к общему знаменателю мы как раз получим левую часть). Переходя к пределу в левой и правой части этого равенства, получим
(приводя правую часть к общему знаменателю мы как раз получим левую часть). Переходя к пределу в левой и правой части этого равенства, получим 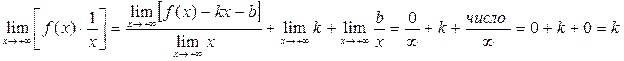 . Первое из требуемых равенств получили. Получим второе. Представим
. Первое из требуемых равенств получили. Получим второе. Представим 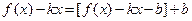 . Переходим к пределу в левой и правой части:
. Переходим к пределу в левой и правой части: 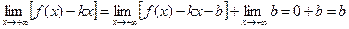 . Что и требовалось доказать.
. Что и требовалось доказать.
Итак, коэффициенты уравнения 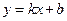 наклонной асимптоты графика функции
наклонной асимптоты графика функции  при
при  находятся по формулам:
находятся по формулам:
(3) 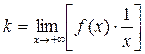 ,
, 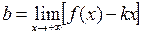 .
.
Если хотя бы один из этих пределов не существует (или равен ∞), то наклонной асимптоты при  у графика нет.
у графика нет.
Что касается наклонной асимптоты при  , то для нее можно повторить все, что сказано для наклонной асимптоты при
, то для нее можно повторить все, что сказано для наклонной асимптоты при  , но во всех пределах надо заменить
, но во всех пределах надо заменить  на
на  . В частности, коэффициенты уравнения
. В частности, коэффициенты уравнения 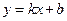 наклонной асимптоты графика функции
наклонной асимптоты графика функции  при
при  находятся по формулам
находятся по формулам 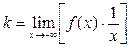 ,
, 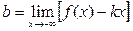 . Если хотя бы один из этих пределов не существует (или равен ∞), то наклонной асимптоты при
. Если хотя бы один из этих пределов не существует (или равен ∞), то наклонной асимптоты при  у графика нет. При поиске наклонных асимптот графика необходимо искать уравнение обеих асимптот (при
у графика нет. При поиске наклонных асимптот графика необходимо искать уравнение обеих асимптот (при  и
и  ). Но для одного класса функций в этом необходимости нет. Доказано, что если функция представляет собой отношение двух многочленов, то ее асимптоты (если они есть) при
). Но для одного класса функций в этом необходимости нет. Доказано, что если функция представляет собой отношение двух многочленов, то ее асимптоты (если они есть) при  и
и  совпадают. В этом случае асимптота, найденная при
совпадают. В этом случае асимптота, найденная при  будет являться и асимптотой при
будет являться и асимптотой при  .
.
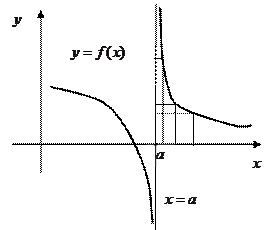 Перейдем теперь к изучению вертикальных асимптот, т.е. вертикальных прямых, к которым «бесконечно близко примыкает график функции при удалении точки графика в бесконечность». Попробуем снова дать математическое определение вертикальной асимптоте. Любая вертикальная прямая имеет уравнение вида
Перейдем теперь к изучению вертикальных асимптот, т.е. вертикальных прямых, к которым «бесконечно близко примыкает график функции при удалении точки графика в бесконечность». Попробуем снова дать математическое определение вертикальной асимптоте. Любая вертикальная прямая имеет уравнение вида 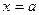 , где
, где  − то число, в котором вертикальная прямая пересекает ось х. Допустим, что такая прямая является вертикальной асимптотой. Для бесконечно близкого приближения графика к такой прямой необходимо, чтобы график хотя бы с одной стороны от этой прямой при подходе к ней резко шел вверх или вниз. Других вариантов нет. Один из возможных вариантов приведен на рисунке. Что же означает такое поведение графика? Если мы начнем приближаться значениями
− то число, в котором вертикальная прямая пересекает ось х. Допустим, что такая прямая является вертикальной асимптотой. Для бесконечно близкого приближения графика к такой прямой необходимо, чтобы график хотя бы с одной стороны от этой прямой при подходе к ней резко шел вверх или вниз. Других вариантов нет. Один из возможных вариантов приведен на рисунке. Что же означает такое поведение графика? Если мы начнем приближаться значениями  к числу
к числу  с правой стороны (как при вычислении правого предела) и каждый раз по графику будем следить за соответствующими значениями функции (см. рисунок), то видно, что значения функции стремятся к +∞. Это означает, что правый предел
с правой стороны (как при вычислении правого предела) и каждый раз по графику будем следить за соответствующими значениями функции (см. рисунок), то видно, что значения функции стремятся к +∞. Это означает, что правый предел 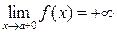 . Аналогично, можно показать, что для функции, график которой изображен на рисунке, левый предел
. Аналогично, можно показать, что для функции, график которой изображен на рисунке, левый предел 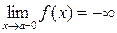 . Бесконечность (+ или −) хотя бы одного такого одностороннего предела и означает безграничное приближение графика к вертикальной прямой с уравнением
. Бесконечность (+ или −) хотя бы одного такого одностороннего предела и означает безграничное приближение графика к вертикальной прямой с уравнением 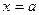 хотя бы с одной стороны. То есть то, что мы и хотели от вертикальной асимптоты. Поэтому естественно принять следующее определение вертикальной асимптоты. Прямая с уравнением
хотя бы с одной стороны. То есть то, что мы и хотели от вертикальной асимптоты. Поэтому естественно принять следующее определение вертикальной асимптоты. Прямая с уравнением 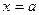 называется вертикальной асимптотой графика функции
называется вертикальной асимптотой графика функции 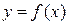 , если выполняется хотя бы одно из условий:
, если выполняется хотя бы одно из условий: 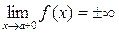 или
или 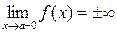 . Поэтому для доказательства того, что некоторая прямая с уравнением
. Поэтому для доказательства того, что некоторая прямая с уравнением 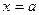 является вертикальной асимптотой, необходимо считать такие пределы. Если хотя бы один из них равен
является вертикальной асимптотой, необходимо считать такие пределы. Если хотя бы один из них равен 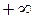 или
или 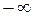 , то прямая есть вертикальная асимптота. Иначе − нет. Как же все-таки находить вертикальные асимптоты графика заданной функции
, то прямая есть вертикальная асимптота. Иначе − нет. Как же все-таки находить вертикальные асимптоты графика заданной функции 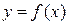 ? Невозможно же для каждого числа
? Невозможно же для каждого числа  на числовой оси х считать оба односторонних предела, чтобы понять, будет ли проходящая через это число вертикальная прямая являться вертикальной асимптотой. Необходимо как-то ограничить количество точек
на числовой оси х считать оба односторонних предела, чтобы понять, будет ли проходящая через это число вертикальная прямая являться вертикальной асимптотой. Необходимо как-то ограничить количество точек  на оси х, подозрительных на прохождение через них вертикальных асимптот. Из приведенного определения вертикальных асимптот следует, что если прямая с уравнением
на оси х, подозрительных на прохождение через них вертикальных асимптот. Из приведенного определения вертикальных асимптот следует, что если прямая с уравнением 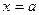 есть вертикальная асимптота, то точка
есть вертикальная асимптота, то точка  обязательно есть точка разрыва функции
обязательно есть точка разрыва функции 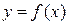 , причем второго рода (односторонние пределы бесконечны). Поэтому проверять нужно только точки разрыва функции. У нас было (при изучении непрерывности функции), что если функция
, причем второго рода (односторонние пределы бесконечны). Поэтому проверять нужно только точки разрыва функции. У нас было (при изучении непрерывности функции), что если функция 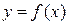 задана одной формулой (т.е. является элементарной функцией), то она непрерывна в точках области определения, а потому точки ее разрыва лежат на границе области определения. Поэтому получаем следующее правило: проверять на вертикальные асимптоты графика функции
задана одной формулой (т.е. является элементарной функцией), то она непрерывна в точках области определения, а потому точки ее разрыва лежат на границе области определения. Поэтому получаем следующее правило: проверять на вертикальные асимптоты графика функции 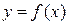 можно только такие прямые с уравнением
можно только такие прямые с уравнением 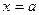 , у которых число
, у которых число  лежит на границе области определения функции. Напомним, что граничными точками некоторого множества называются такие точки, в любой окрестности которых есть точки как принадлежащие этому множеству, так и ему не принадлежащие. Поэтому упомянутые выше граничные точки области определения функции
лежит на границе области определения функции. Напомним, что граничными точками некоторого множества называются такие точки, в любой окрестности которых есть точки как принадлежащие этому множеству, так и ему не принадлежащие. Поэтому упомянутые выше граничные точки области определения функции 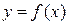 это точки, в любой окрестности которых есть как точки области определения функция, так и точки, в нее не входящие.
это точки, в любой окрестности которых есть как точки области определения функция, так и точки, в нее не входящие.
Пример 1. Найти асимптоты графика функции 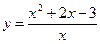 .
.
Решение.
1) Находим наклонные асимптоты. Вычисляем  и
и  для наклонной асимптоты
для наклонной асимптоты 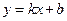 при
при  по формулам (1):
по формулам (1): 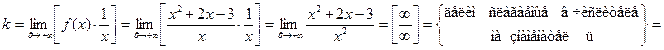
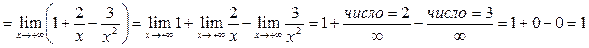 . Итак,
. Итак, 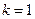 . Далее,
. Далее,
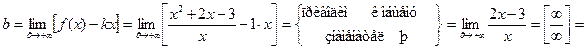
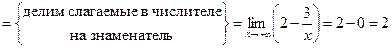 . Итак,
. Итак, 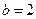 . Поэтому уравнение наклонной асимптоты при
. Поэтому уравнение наклонной асимптоты при  :
: 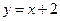 . Поскольку исследуемая функция
. Поскольку исследуемая функция 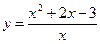 представляет собой отношение двух многочленов (второй и первой степени), то, как сказано выше, эта же прямая будет наклонной асимптотой и при
представляет собой отношение двух многочленов (второй и первой степени), то, как сказано выше, эта же прямая будет наклонной асимптотой и при  .
.
2) Найдем вертикальные асимптоты. Их уравнение имеет вид 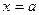 , причем (по приведенному выше правилу) число
, причем (по приведенному выше правилу) число  может лежать только на границе области определения функции. Поскольку область определения функции
может лежать только на границе области определения функции. Поскольку область определения функции 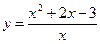 есть
есть 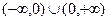 , то граничной точкой такой области является только число 0, поскольку в любой окрестности этой точки есть точки как из области определения, так и не из нее (это сама точка 0). Поэтому проверяем только
, то граничной точкой такой области является только число 0, поскольку в любой окрестности этой точки есть точки как из области определения, так и не из нее (это сама точка 0). Поэтому проверяем только  . Это значит, что проверяется на вертикальную асимптоту прямая с уравнением
. Это значит, что проверяется на вертикальную асимптоту прямая с уравнением  (эта прямая, как известно, совпадает с осью у). Считаем односторонние пределы при
(эта прямая, как известно, совпадает с осью у). Считаем односторонние пределы при 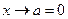 :
: 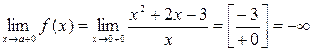 . Дробь
. Дробь 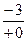 означает, что при подстановке вместо
означает, что при подстановке вместо  числа 0 в числителе получается число
числа 0 в числителе получается число 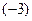 , а в знаменателе 0, к которому пришли со стороны положительных чисел. При изучении псевдонеопределенностей мы получали, что
, а в знаменателе 0, к которому пришли со стороны положительных чисел. При изучении псевдонеопределенностей мы получали, что 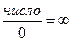 . Осталось понять, почему мы поставили знак минус у этой бесконечности. При
. Осталось понять, почему мы поставили знак минус у этой бесконечности. При  , близких к 0 со стороны положительных чисел, выяснилось, что числитель приближается к числу
, близких к 0 со стороны положительных чисел, выяснилось, что числитель приближается к числу 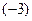 (т.е. становится отрицательным), а знаменатель положителен. Поэтому вся дробь
(т.е. становится отрицательным), а знаменатель положителен. Поэтому вся дробь 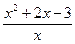 под знаком предела отрицательна. Поэтому получилась именно (−∞). Аналогично получаем для левого предела
под знаком предела отрицательна. Поэтому получилась именно (−∞). Аналогично получаем для левого предела 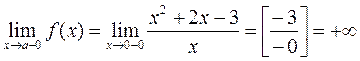 . Итак, получили
. Итак, получили 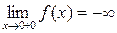 ,
, 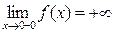 . Так как оба односторонних предела равны бесконечности, то (по определению) прямая с уравнением
. Так как оба односторонних предела равны бесконечности, то (по определению) прямая с уравнением  (т.е. ось у) является вертикальной асимптотой. На рисунке схематично изображен график исследуемой функции, видно поведение графика вблизи асимптот.
(т.е. ось у) является вертикальной асимптотой. На рисунке схематично изображен график исследуемой функции, видно поведение графика вблизи асимптот.
Пример 2. Найти асимптоты графика функции 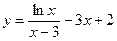 .
.
Решение. Прежде всего, найдем область определения, которая в данном примере играет существенную роль. Поскольку в правой части формулы 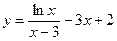 переменная
переменная  встречается под знаком логарифма, то она должна быть строго положительной:
встречается под знаком логарифма, то она должна быть строго положительной: 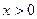 . С другой стороны, при вычислении значения функции присутствует операция деления на
. С другой стороны, при вычислении значения функции присутствует операция деления на 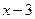 . Поскольку на 0 делить нельзя, то исключаем из возможных значение
. Поскольку на 0 делить нельзя, то исключаем из возможных значение 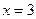 . Таким образом, область определения данной функции − все положительные числа, за
. Таким образом, область определения данной функции − все положительные числа, за
исключением числа 3, т.е. объединение двух интервалов: 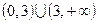 . Поскольку (как мы только что выяснили)
. Поскольку (как мы только что выяснили)  не может принимать отрицательные значения, то это означает, что над отрицательной частью оси
не может принимать отрицательные значения, то это означает, что над отрицательной частью оси  график этой функции вообще отсутствует, а потому у него (графика то есть) не может быть никакой асимптоты при
график этой функции вообще отсутствует, а потому у него (графика то есть) не может быть никакой асимптоты при  . Далее двигаемся по схеме решения предыдущего примера.
. Далее двигаемся по схеме решения предыдущего примера.


 лучше всего характеризует характер зависимости некоторого фактора
лучше всего характеризует характер зависимости некоторого фактора  от другого фактора
от другого фактора  , задаваемой этой функцией. На графике сразу видно, где функция возрастает, а где убывает и насколько быстро, сразу видны ее экстремумы, интервалы положительности и отрицательности ее значений и т.д.. Чего не скажешь, глядя на саму формулу
, задаваемой этой функцией. На графике сразу видно, где функция возрастает, а где убывает и насколько быстро, сразу видны ее экстремумы, интервалы положительности и отрицательности ее значений и т.д.. Чего не скажешь, глядя на саму формулу  функции, помогающие достаточно точно строить ее график. Рассмотрим некоторую функцию
функции, помогающие достаточно точно строить ее график. Рассмотрим некоторую функцию  функция возрастает. Это означает, что при рисовании графика должны вести его строго вверх между точками А и В (с координатами
функция возрастает. Это означает, что при рисовании графика должны вести его строго вверх между точками А и В (с координатами 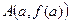 и
и 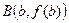 ). Но сделать это можно по-разному (см. рисунок): либо провести график выпуклостью вверх или вниз. Как же определить направление выпуклости. Первая производная (которая указала нам просто на возрастание функции) ответа уже не даст. В данном случае ответ даст уже вторая производная. Сначала заметим (по рисунку), что если кривая имеет выпуклость вверх, то она расположена под касательной, проведенной к любой из ее точек. А если выпуклость направлена вниз, то над касательной. Поэтому примем такие определения. Будем говорить, что график функции
). Но сделать это можно по-разному (см. рисунок): либо провести график выпуклостью вверх или вниз. Как же определить направление выпуклости. Первая производная (которая указала нам просто на возрастание функции) ответа уже не даст. В данном случае ответ даст уже вторая производная. Сначала заметим (по рисунку), что если кривая имеет выпуклость вверх, то она расположена под касательной, проведенной к любой из ее точек. А если выпуклость направлена вниз, то над касательной. Поэтому примем такие определения. Будем говорить, что график функции  ниже (выше) любой касательной к графику функции на
ниже (выше) любой касательной к графику функции на 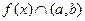
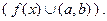 Каким же образом вторая производная покажет направление выпуклости графика? Обратимся к рисунку, на котором график функции
Каким же образом вторая производная покажет направление выпуклости графика? Обратимся к рисунку, на котором график функции  и
и  из
из 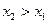 . Построим касательные в соответствующих точках графика (на рисунке). Пусть касательная в точке графика с координатой
. Построим касательные в соответствующих точках графика (на рисунке). Пусть касательная в точке графика с координатой  , а касательная с координатой
, а касательная с координатой 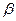 . Из геометрического смысла производной ясно, что
. Из геометрического смысла производной ясно, что 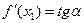 , а
, а 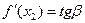 . Из рисунка видно, что при выпуклости графика вверх угол
. Из рисунка видно, что при выпуклости графика вверх угол 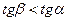 , т.е.
, т.е. 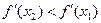 . Таким образом, выяснено, что большему значению х соответствует меньшее значение функции
. Таким образом, выяснено, что большему значению х соответствует меньшее значение функции  . Это (по определению) означает, что функция
. Это (по определению) означает, что функция 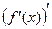 ) должна быть отрицательной на этом интервале. Но по определению производная от производной и есть вторая производная:
) должна быть отрицательной на этом интервале. Но по определению производная от производной и есть вторая производная: 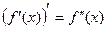 . Итак, мы доказали (точнее, показали), что если график функции имеет на некотором интервале выпуклость вверх, то вторая производная этой функции (если она, конечно, существует) является отрицательной (точнее, неположительной). Аналогично можно доказать-показать, что если график функции имеет на некотором интервале выпуклость вниз, то его вторая производная положительна (точнее, неотрицательна). Итак, справедлива
. Итак, мы доказали (точнее, показали), что если график функции имеет на некотором интервале выпуклость вверх, то вторая производная этой функции (если она, конечно, существует) является отрицательной (точнее, неположительной). Аналогично можно доказать-показать, что если график функции имеет на некотором интервале выпуклость вниз, то его вторая производная положительна (точнее, неотрицательна). Итак, справедлива . Тогда если
. Тогда если 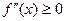 (
(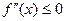 )на
)на 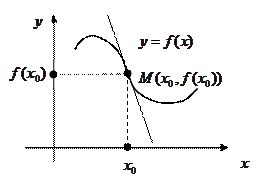 Прейдем теперь к так называемым точкам перегиба графика. Ранее точки экстремума (максимумы и минимумы) обычно разделяли участки монотонности функции разного вида (возрастание − убывание, убывание − возрастание). Аналогично, участки графика, имеющие разное направление выпуклости, тоже обычно разделяются некоторой характерной точкой графика, которая называется точкой перегиба (см. рисунок). Дадим определение такой точки. Точка
Прейдем теперь к так называемым точкам перегиба графика. Ранее точки экстремума (максимумы и минимумы) обычно разделяли участки монотонности функции разного вида (возрастание − убывание, убывание − возрастание). Аналогично, участки графика, имеющие разное направление выпуклости, тоже обычно разделяются некоторой характерной точкой графика, которая называется точкой перегиба (см. рисунок). Дадим определение такой точки. Точка  графика функции
графика функции 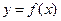 называется точкой перегиба, если выполнены условия:
называется точкой перегиба, если выполнены условия: Требование существования касательной в точке перегиба продиктовано тем, что в точке перегиба переход от одного направления выпуклости к другому должен проходить «гладко» (перегиб, а не перелом). Отсутствие касательной, как было сказано раньше, ведет к появлению точки излома графика. Такая точка не считается точкой перегиба, даже если она действительно разделяет разные направления выпуклости графика (такова точка
Требование существования касательной в точке перегиба продиктовано тем, что в точке перегиба переход от одного направления выпуклости к другому должен проходить «гладко» (перегиб, а не перелом). Отсутствие касательной, как было сказано раньше, ведет к появлению точки излома графика. Такая точка не считается точкой перегиба, даже если она действительно разделяет разные направления выпуклости графика (такова точка  существует и непрерывна вторая производная функции
существует и непрерывна вторая производная функции 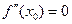 .
.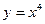 . Ее график имеет ту же форму, что и парабола
. Ее график имеет ту же форму, что и парабола  , но ветви у него круче идут вверх (см. рисунок). Точек перегиба у него нет, так как ее график имеет выпуклость вниз на всей числовой прямой (ее вторая производная равна
, но ветви у него круче идут вверх (см. рисунок). Точек перегиба у него нет, так как ее график имеет выпуклость вниз на всей числовой прямой (ее вторая производная равна 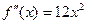 , а потому везде положительна). Однако ясно, что вторая производная обращается в 0 при
, а потому везде положительна). Однако ясно, что вторая производная обращается в 0 при  , а потому
, а потому 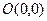 − не точка перегиба. Поэтому для исследования произвольных функций опять нужен алгоритм, позволяющий отсеивать критические точки функции 2 рода, не дающие перегиб. Такой алгоритм прост и нагляден.
− не точка перегиба. Поэтому для исследования произвольных функций опять нужен алгоритм, позволяющий отсеивать критические точки функции 2 рода, не дающие перегиб. Такой алгоритм прост и нагляден. Теорема (достаточное условие точки перегиба). Пусть функция
Теорема (достаточное условие точки перегиба). Пусть функция  в самой точке
в самой точке 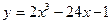 на выпуклость и точки перегиба.
на выпуклость и точки перегиба.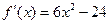 ,
, 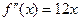 . Вторая производная существует на всей числовой прямой и обращается в 0 только при
. Вторая производная существует на всей числовой прямой и обращается в 0 только при 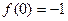 . Поэтому
. Поэтому 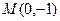 − единственная точка графика функции, подозрительная на точку перегиба этого графика. По аналогии с исследованием
− единственная точка графика функции, подозрительная на точку перегиба этого графика. По аналогии с исследованием 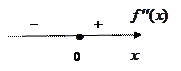 функции на монотонность и экстремумы наносим точку
функции на монотонность и экстремумы наносим точку 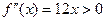 при
при 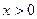 и
и 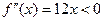 при
при 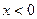 . Поэтому
. Поэтому 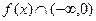 и
и 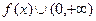 . Точка
. Точка  Пример 2. Исследовать график функции
Пример 2. Исследовать график функции 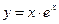 на выпуклость и точки перегиба.
на выпуклость и точки перегиба.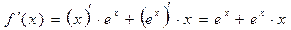 . Тогда вторая производная:
. Тогда вторая производная: 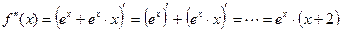 . Она существует на всей числовой прямой и обращается в 0 только при
. Она существует на всей числовой прямой и обращается в 0 только при  (так как функция
(так как функция 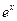 не обращается в 0 ни при каких значениях
не обращается в 0 ни при каких значениях 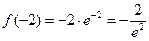 . Поэтому
. Поэтому 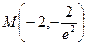 − единственная точка графика функции, подозрительная на точку перегиба. Наносим точку
− единственная точка графика функции, подозрительная на точку перегиба. Наносим точку 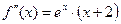 на получившихся интервалах. Поскольку экспонента
на получившихся интервалах. Поскольку экспонента 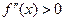 при
при 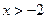 и
и 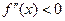 при
при 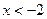 . Поэтому
. Поэтому 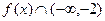 и
и 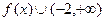 . Точка
. Точка 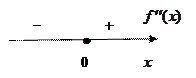 Пример 3. Провести аналогичное исследование для функции
Пример 3. Провести аналогичное исследование для функции 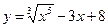 . Решение. Ищем критические точки 2 рода. Первая производная:
. Решение. Ищем критические точки 2 рода. Первая производная: 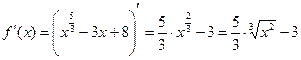 . Тогда вторая производная:
. Тогда вторая производная: 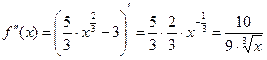 . Она не существует только при
. Она не существует только при 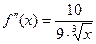 ни при каких значениях
ни при каких значениях 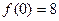 . Поэтому
. Поэтому 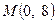 − единственная точка графика функции, подозрительная на точку перегиба. Наносим точку
− единственная точка графика функции, подозрительная на точку перегиба. Наносим точку 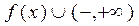 . Точка
. Точка 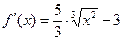 . Поэтому по замечанию к теореме о достаточном условии точки перегиба точка графика
. Поэтому по замечанию к теореме о достаточном условии точки перегиба точка графика  и
и  ) или вблизи точек разрыва второго рода часто оказывается, что график функции сколь угодно близко приближается к некоторым характерным прямым. Такие прямые называются асимптотами графика функции. Понятно, что если бы мы научились находить такие прямые, то это нам очень бы помогло для более точного построения графика. Прямые на координатной плоскости могут быть вертикальными (параллельными оси у) и наклонными (в частности, горизонтальными). В зависимости от того, к какой из них приближается график функции, будем различать вертикальные и наклонные асимптоты.
) или вблизи точек разрыва второго рода часто оказывается, что график функции сколь угодно близко приближается к некоторым характерным прямым. Такие прямые называются асимптотами графика функции. Понятно, что если бы мы научились находить такие прямые, то это нам очень бы помогло для более точного построения графика. Прямые на координатной плоскости могут быть вертикальными (параллельными оси у) и наклонными (в частности, горизонтальными). В зависимости от того, к какой из них приближается график функции, будем различать вертикальные и наклонные асимптоты. Изучим сначала наклонные асимптоты. Как видно из рисунка, график функции может приближаться к различным прямым при
Изучим сначала наклонные асимптоты. Как видно из рисунка, график функции может приближаться к различным прямым при 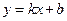 . Меняя числа
. Меняя числа  и
и  , получим уравнения всех наклонных прямых. При некоторой паре чисел
, получим уравнения всех наклонных прямых. При некоторой паре чисел 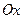 (мы потом устремим
(мы потом устремим 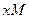 есть не что иное, как значение функции в точке
есть не что иное, как значение функции в точке 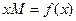 . Поскольку точка
. Поскольку точка  лежит на асимптоте с уравнением
лежит на асимптоте с уравнением 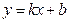 , то длина отрезка
, то длина отрезка 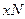 есть значение функции
есть значение функции 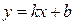 в текущей точке
в текущей точке 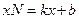 . Поэтому длина отрезка
. Поэтому длина отрезка 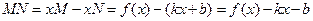 . По рисунку расстояние от точки
. По рисунку расстояние от точки 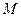 графика до асимптоты (которое и должно по нашему мнению стремиться к 0 при
графика до асимптоты (которое и должно по нашему мнению стремиться к 0 при 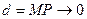 при
при 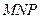 находим
находим 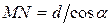 . Поэтому
. Поэтому 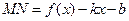 стремится к 0 при
стремится к 0 при  Наклонная прямая с уравнением
Наклонная прямая с уравнением 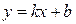 называется наклонной асимптотой графика функции
называется наклонной асимптотой графика функции 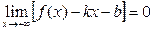 .
. : прямая с уравнением
: прямая с уравнением 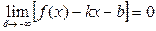 .
. Теперь, после введения строгого определения, вернемся к вопросу о нахождении формул для чисел
Теперь, после введения строгого определения, вернемся к вопросу о нахождении формул для чисел 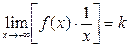 ,
, 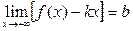 .
.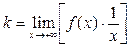 ,
, 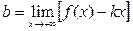 . Поскольку прямая
. Поскольку прямая 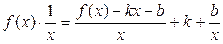 (приводя правую часть к общему знаменателю мы как раз получим левую часть). Переходя к пределу в левой и правой части этого равенства, получим
(приводя правую часть к общему знаменателю мы как раз получим левую часть). Переходя к пределу в левой и правой части этого равенства, получим 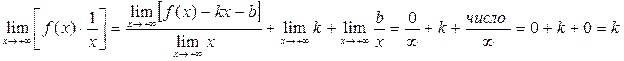 . Первое из требуемых равенств получили. Получим второе. Представим
. Первое из требуемых равенств получили. Получим второе. Представим 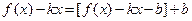 . Переходим к пределу в левой и правой части:
. Переходим к пределу в левой и правой части: 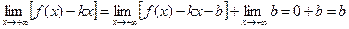 . Что и требовалось доказать.
. Что и требовалось доказать.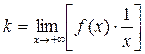 ,
, 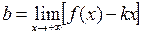 .
.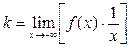 ,
, 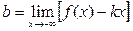 . Если хотя бы один из этих пределов не существует (или равен ∞), то наклонной асимптоты при
. Если хотя бы один из этих пределов не существует (или равен ∞), то наклонной асимптоты при  Перейдем теперь к изучению вертикальных асимптот, т.е. вертикальных прямых, к которым «бесконечно близко примыкает график функции при удалении точки графика в бесконечность». Попробуем снова дать математическое определение вертикальной асимптоте. Любая вертикальная прямая имеет уравнение вида
Перейдем теперь к изучению вертикальных асимптот, т.е. вертикальных прямых, к которым «бесконечно близко примыкает график функции при удалении точки графика в бесконечность». Попробуем снова дать математическое определение вертикальной асимптоте. Любая вертикальная прямая имеет уравнение вида 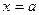 , где
, где  − то число, в котором вертикальная прямая пересекает ось х. Допустим, что такая прямая является вертикальной асимптотой. Для бесконечно близкого приближения графика к такой прямой необходимо, чтобы график хотя бы с одной стороны от этой прямой при подходе к ней резко шел вверх или вниз. Других вариантов нет. Один из возможных вариантов приведен на рисунке. Что же означает такое поведение графика? Если мы начнем приближаться значениями
− то число, в котором вертикальная прямая пересекает ось х. Допустим, что такая прямая является вертикальной асимптотой. Для бесконечно близкого приближения графика к такой прямой необходимо, чтобы график хотя бы с одной стороны от этой прямой при подходе к ней резко шел вверх или вниз. Других вариантов нет. Один из возможных вариантов приведен на рисунке. Что же означает такое поведение графика? Если мы начнем приближаться значениями 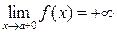 . Аналогично, можно показать, что для функции, график которой изображен на рисунке, левый предел
. Аналогично, можно показать, что для функции, график которой изображен на рисунке, левый предел 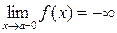 . Бесконечность (+ или −) хотя бы одного такого одностороннего предела и означает безграничное приближение графика к вертикальной прямой с уравнением
. Бесконечность (+ или −) хотя бы одного такого одностороннего предела и означает безграничное приближение графика к вертикальной прямой с уравнением 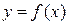 , если выполняется хотя бы одно из условий:
, если выполняется хотя бы одно из условий: 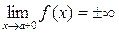 или
или 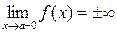 . Поэтому для доказательства того, что некоторая прямая с уравнением
. Поэтому для доказательства того, что некоторая прямая с уравнением 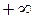 или
или 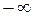 , то прямая есть вертикальная асимптота. Иначе − нет. Как же все-таки находить вертикальные асимптоты графика заданной функции
, то прямая есть вертикальная асимптота. Иначе − нет. Как же все-таки находить вертикальные асимптоты графика заданной функции 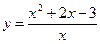 .
.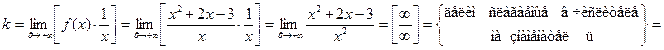
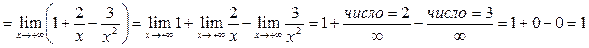 . Итак,
. Итак, 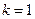 . Далее,
. Далее,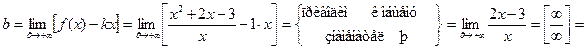
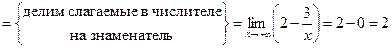 . Итак,
. Итак, 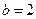 . Поэтому уравнение наклонной асимптоты при
. Поэтому уравнение наклонной асимптоты при 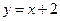 . Поскольку исследуемая функция
. Поскольку исследуемая функция 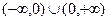 , то граничной точкой такой области является только число 0, поскольку в любой окрестности этой точки есть точки как из области определения, так и не из нее (это сама точка 0). Поэтому проверяем только
, то граничной точкой такой области является только число 0, поскольку в любой окрестности этой точки есть точки как из области определения, так и не из нее (это сама точка 0). Поэтому проверяем только  . Это значит, что проверяется на вертикальную асимптоту прямая с уравнением
. Это значит, что проверяется на вертикальную асимптоту прямая с уравнением 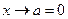 :
: 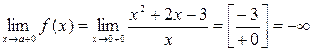 . Дробь
. Дробь 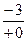 означает, что при подстановке вместо
означает, что при подстановке вместо 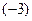 , а в знаменателе 0, к которому пришли со стороны положительных чисел. При изучении псевдонеопределенностей мы получали, что
, а в знаменателе 0, к которому пришли со стороны положительных чисел. При изучении псевдонеопределенностей мы получали, что 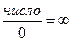 . Осталось понять, почему мы поставили знак минус у этой бесконечности. При
. Осталось понять, почему мы поставили знак минус у этой бесконечности. При  , близких к 0 со стороны положительных чисел, выяснилось, что числитель приближается к числу
, близких к 0 со стороны положительных чисел, выяснилось, что числитель приближается к числу 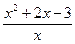 под знаком предела отрицательна. Поэтому получилась именно (−∞). Аналогично получаем для левого предела
под знаком предела отрицательна. Поэтому получилась именно (−∞). Аналогично получаем для левого предела 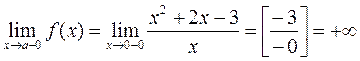 . Итак, получили
. Итак, получили 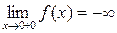 ,
, 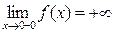 . Так как оба односторонних предела равны бесконечности, то (по определению) прямая с уравнением
. Так как оба односторонних предела равны бесконечности, то (по определению) прямая с уравнением 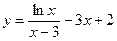 .
.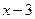 . Поскольку на 0 делить нельзя, то исключаем из возможных значение
. Поскольку на 0 делить нельзя, то исключаем из возможных значение 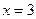 . Таким образом, область определения данной функции − все положительные числа, за
. Таким образом, область определения данной функции − все положительные числа, за 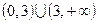 . Поскольку (как мы только что выяснили)
. Поскольку (как мы только что выяснили) 


