
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Допускающие понижение порядка
Сведения из теории
Укажем несколько типов дифференциальных уравнений, которые заменой переменных можно свести к уравнениям меньшего порядка.
10.1.1. Простейшее дифференциальное уравнение n -го порядка Это уравнение вида
…………..
10.1.2. Уравнение n -го порядка, не содержащее явно искомой функции и ее производных до
Его можно рассматривать как уравнение
Пусть
k -кратным интегрированием, в соответствии с п. 10.1.1.
Уравнение второго порядка, не содержащее явно независимой переменной x
Введем новую неизвестную функцию
Дифференцируя по
Подставляя выражения
Пусть
Аналогично, уравнение Примеры решения задач 10.2.1. Решить уравнение ◄
10.2.2. Решить уравнение ◄ Уравнение не содержит явно
Замечание. При решении задачи Коши значения постоянных
10.2.3. Найти общее решение дифференциального уравнения ◄ Уравнение не содержит явно независимой переменной
Таким образом, Найдем теперь решение, удовлетворяющее начальным условиям
Подставляя в полученное соотношение начальные данные
Приведем теперь другой вариант решения задачи Коши, в котором используются определенные интегралы. Для функции начального условия 10.3. Задачи для самостоятельного решения Решить уравнения.
11. Линейные однородные дифференциальные уравнения n- го порядка Сведения из теории Система функций
называется линейно независимой, если равенство
имеет место только при Определителем Вронского системы функций называется определитель n -го порядка
Если Уравнение вида
называется линейным однородным дифференциальным уравнением n-го порядка. Фундаментальной системой решений (ф.с.р.) уравнения называется система
где Примеры решения задач 11.2.1. Убедиться, что функции
образуют фундаментальную систему решений уравнения
Найти общее решение уравнения. ◄ 1) То, что функции решения уравнения легко проверить их подстановкой в уравнение. 2) Проверим линейную независимость системы функций: a. Определитель Вронского
Следовательно, функции линейно независимы. b. Линейную независимость системы можно проверить и исходя из определения. Пусть
Полагая
Решая эту систему, находим 3) Общее решение уравнения имеет вид
11.3. Задачи для самостоятельного решения Убедиться, что заданная система функций образует фундаментальную систему решений линейного дифференциального уравнения. Найти общее решение.
11.3.1.
11.3.2.
11.3.3. Известно, что для функций
|
||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 341; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.104.29 (0.025 с.) |
 . Его общее решение находится n- кратным интегрированием
. Его общее решение находится n- кратным интегрированием ,
, ,
, .
. -го порядка включительно
-го порядка включительно .
. -го порядка относительно функции
-го порядка относительно функции  :
: .
. – его общее решение. Тогда общее решение
– его общее решение. Тогда общее решение  уравнения находится из уравнения
уравнения находится из уравнения
 .
. , связанную с
, связанную с  соотношением
соотношением .
. и используя правило дифференцирования сложной функции, находим
и используя правило дифференцирования сложной функции, находим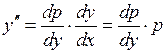 .
. и
и  в, получим уравнение первого порядка для функции
в, получим уравнение первого порядка для функции 
 .
. – его общее решение. Общее решение
– его общее решение. Общее решение 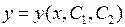 уравнения находим, решая уравнение с разделяющимися переменными
уравнения находим, решая уравнение с разделяющимися переменными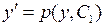 .
. можно свести к уравнению
можно свести к уравнению  -го порядка для функции
-го порядка для функции  .
. .
. .
. .
. .►
.► .
. и
и  , тогда
, тогда  .
.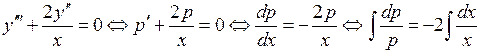 .
. .
. .►
.► целесообразно находить последовательно в процессе решения, а не после нахождения общего решения.
целесообразно находить последовательно в процессе решения, а не после нахождения общего решения.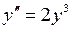 , и решение, удовлетворяющее начальным условиям
, и решение, удовлетворяющее начальным условиям  .
. . Подставив это выражение в уравнение, получим уравнение с разделяющимися переменными для функции
. Подставив это выражение в уравнение, получим уравнение с разделяющимися переменными для функции 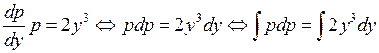

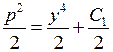 .
. и для функции y получаем дифференциальное уравнение с разделяющимися переменными
и для функции y получаем дифференциальное уравнение с разделяющимися переменными  . Его общий интеграл имеет вид
. Его общий интеграл имеет вид  . Заметим, что левая часть этого уравнения не выражается через элементарные функции.
. Заметим, что левая часть этого уравнения не выражается через элементарные функции. , получаем
, получаем  . Теперь
. Теперь  . Выбираем знак «+», так как
. Выбираем знак «+», так как  . Для нахождения искомого решения получаем уравнение
. Для нахождения искомого решения получаем уравнение .
.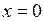 и
и  , находим, что
, находим, что 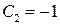 . В итоге получаем решение задачи Коши
. В итоге получаем решение задачи Коши .
. имеем дифференциальное уравнение
имеем дифференциальное уравнение  и начальное условие
и начальное условие  . Поэтому
. Поэтому  и, следовательно,
и, следовательно,  . Теперь из уравнения
. Теперь из уравнения  и
и получаем
получаем 

 .►
.► .
.
 .
.
 .
10.3.4.
.
10.3.4.  .
.
 .
10.3.6.
.
10.3.6.  .
.

 .
.
 ,
,
 .
.
 .
.
 .
.
 .
.
 ,
,  .
.
 ,
, 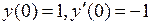 .
.
 ,
,  .
.
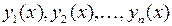 ,
,  ,
,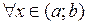

 .
. .
. хотя бы в одной точке
хотя бы в одной точке 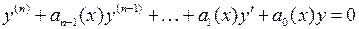
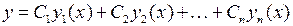 ,
, ,
, .
.
 .
.
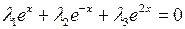 .
. , получим
, получим
 , то есть система функций линейно независима.
, то есть система функций линейно независима. .►
.► ,
,  .
. ,
,  .
. определитель Вронского в точке
определитель Вронского в точке  равен нулю, а в точке
равен нулю, а в точке  не равен нулю. Можно ли что-нибудь сказать о линейной зависимости (или независимости) этих функций на отрезке
не равен нулю. Можно ли что-нибудь сказать о линейной зависимости (или независимости) этих функций на отрезке  ?
?


