
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Случайные погрешности измерений
Факторы, определяющие возникновение случайных погрешностей, проявляются нерегулярно, в различных комбинациях и с интенсивностью, которую трудно предвидеть. Случайная погрешность случайно изменяется при повторных измерениях одной и той же физической величины. Однако если оперировать исправленными результатами измерений, т.е. такими, из которых исключены систематические погрешности, то чисто случайные погрешности будут обладать следующими свойствами: • равные по абсолютной величине положительные и отрицательные погрешности равновероятны; • большие погрешности наблюдаются реже, чем малые; • с увеличением числа измерений одной и той же величины среднее арифметическое погрешностей стремится к нулю, и, следовательно, среднее арифметическое результатов измерений стремится к истинному значению измеряемой величины. Фактическое значение случайной погрешности, полученное при поверке средства измерения, не характеризует его точности. Для оценки интервала значений погрешностей и вероятности появления определенных значений необходимы многократные измерения и использование математического аппарата теории вероятностей. Наиболее универсальный способ описания случайных величин заключается в отыскании их интегральных или дифференциальных функций распределения. Интегральной функцией распределения
где Р — символ вероятности события, описание которого заключено в фигурных скобках. Обычно график интегральной функции распределения результатов наблюдений представляет собой непрерывную неубывающую кривую, начинающуюся от нуля на отрицательной бесконечности и асимптотически приближающуюся к единице при увеличении аргумента до плюс бесконечности. Если интегральная функция имеет точку перегиба при значении Более наглядным является описание свойств результатов наблюдений, содержащих случайные погрешности, с помощью дифференциальной функции распределения, иначе называемой плотностью распределения вероятностей (рис. 3.3, б):
Поскольку Вероятность попадания случайной величины
Рис. 3.3. Интегральная (а) и дифференциальная (б) функции распределения случайной величины:
Отыскание функций распределения требует проведения весьма трудоемких исследований и вычислений. На практике встречаются трапециидальные, уплощенные, экспоненциальные и другие виды распределений. Однако для наибольшего числа встречающихся на практике случайных величин можно ожидать распределение по так называемому закону нормального распределения (закону Гаусса). Теоретически доказано, что распределение случайных погрешностей будет близко к нормальному всякий раз, когда результаты наблюдений формируются под действием большого числа независимо действующих факторов, каждый из которых оказывает лишь незначительное действие по сравнению с суммарным действием всех остальных. Плотность нормального распределения вероятностей для случайной величины (рис. 3.4, а) описывается уравнением:
где Кривая имеет точки перегиба, соответствующие абсциссам Если данную кривую рассматривают как плотность распределения случайных погрешностей, то начало координат переносят в центр распределения и по оси абсцисс откладывают значения погрешностей
Математическое ожидание случайной величины
представляет собой оценку истинного значения измеряемой величины. Математическое ожидание случайных погрешностей равно нулю. Дисперсия результатов наблюдений является характеристикой их рассеивания:
Она имеет размерность квадрата измеряемой величины и не всегда удобна для использования в качестве характеристики рассеивания. Среднее квадратическое отклонение результатов наблюдений
а
б Рис. 3.4. Кривая нормального распределения случайной величины (а) и случайной погрешности (б): величины;
Если абсцисса функций нормального распределения выражается в долях среднего квадратического отклонения:
и начало координат находится в центре распределения, то распределение называется нормированным. Уравнения дифференциальной и интегральной функций нормированного нормального распределения принимают следующий вид:
Определенный интеграл
называют функцией Лапласа. Заметим, что Значения функции Лапласа для различных значений t приведены в табл. 3.1. Приведенные в табл. 3.1 значения показывают, что случайная погрешность при одноразовом измерении не выйдет за пределы интервала Таблица 3.1 Значения функции Лапласа
В интервале В производственной практике часто считается необходимым выполнение следующего условия: допустимое предельное отклонение от заданного номинального размера должно быть не меньше интервала Область технологического рассеивания какого-либо размера (параметра) изделия, как правило, подчиняется нормальному закону, и периодически определяемое среднее квадратическое отклонение является показателем изменений в технологическом цикле.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-28; просмотров: 491; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.58.150.59 (0.011 с.) |
 называют функцию, значение которой для каждого
называют функцию, значение которой для каждого 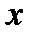 является вероятностью появления значений
является вероятностью появления значений  (в i-м наблюдении), меньших
(в i-м наблюдении), меньших 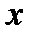 :
: =P
=P 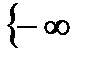

 , близком к истинному значению измеряемой величины, и принимает в этой точке значение, равное 0,5, то говорят о симметричности распределения результатов (рис. 3.3, а).
, близком к истинному значению измеряемой величины, и принимает в этой точке значение, равное 0,5, то говорят о симметричности распределения результатов (рис. 3.3, а).
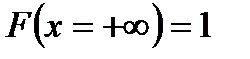 , то
, то  , т.е. площадь, заключенная между кривой дифференциальной функции распределения и осью абсцисс, равна единице.
, т.е. площадь, заключенная между кривой дифференциальной функции распределения и осью абсцисс, равна единице. в заданный интервал (
в заданный интервал ( ) равна площади, заключенной между абсциссами
) равна площади, заключенной между абсциссами  и
и 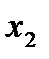 :
:

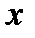 — значения измеряемой величины;
— значения измеряемой величины; 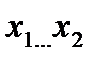 — заданный интервал;
— заданный интервал; 
 — значения интегральной функции в начальной и конечной точках заданного интервала;
— значения интегральной функции в начальной и конечной точках заданного интервала;  — центр распределения;
— центр распределения;  — дифференциальная функция распределения;
— дифференциальная функция распределения;  — площадь, заключенная между кривой дифференциальной функции распределения и осью абсцисс
— площадь, заключенная между кривой дифференциальной функции распределения и осью абсцисс
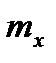 и
и  - математическое ожидание и среднее квадратичное отклонение, являющиеся основными параметрами нормального распределения;
- математическое ожидание и среднее квадратичное отклонение, являющиеся основными параметрами нормального распределения;  - основание натурального логарифма.
- основание натурального логарифма. .
. (рис. 3.4, б). Уравнение принимает вид:
(рис. 3.4, б). Уравнение принимает вид:


 имеет размерность измеряемой величины и наиболее часто используется в качестве основного параметра, характеризующего рассеивание результатов измерений.
имеет размерность измеряемой величины и наиболее часто используется в качестве основного параметра, характеризующего рассеивание результатов измерений.

 — дифференциальная функция распределения случайной
— дифференциальная функция распределения случайной — дифференциальная функция распределения случайной погрешности;
— дифференциальная функция распределения случайной погрешности; — среднее квадратическое отклонение;
— среднее квадратическое отклонение;  — погрешность;
— погрешность; — математическое ожидание
— математическое ожидание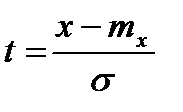

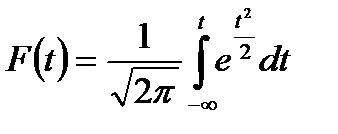 ;
;

 .
. с вероятностью ≈ 0,68 (0,3413·2), т.е. 68% измерений будут иметь погрешность
с вероятностью ≈ 0,68 (0,3413·2), т.е. 68% измерений будут иметь погрешность  .
.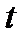
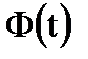
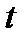
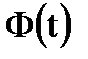
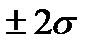 погрешность находится с вероятностью ≈ 0,95 (0,4772·2), в интервале
погрешность находится с вероятностью ≈ 0,95 (0,4772·2), в интервале 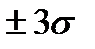 — с вероятностью 0,9973, т.е. вероятность того, что случайная погрешность не выйдет за пределы
— с вероятностью 0,9973, т.е. вероятность того, что случайная погрешность не выйдет за пределы 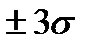 , составляет 0,9973, или 99,73 %. На практике с учетом интервала
, составляет 0,9973, или 99,73 %. На практике с учетом интервала 


