
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Приближенное решение нелинейных уравнений
§2. Правило пропорциональных частей (метод хорд).
Точки А (a; f (a)) и В (b; f(b)) соединим хордой. Найдем точку х1 :
Если f (х1) < 0, то за новый, более узкий, интервал изоляции можно взять отрезок[ х1; b]. Соединив точки А1 (х1; f (х1)) и В (b; f(b)), получим в точке пересечения хорды с осью второе приближение х2, которое вычислим по формуле:
и т. д. Последовательность чисел а, х1, х2.... стремится к искомому корню х0. Вычисления следует вести до тех пор, пока не перестанут изменяться те десятичные знаки, которые мы хотим сохранить в ответе (т.е. пока не будет достигнута заданная степень точности). Пример 1.2: Методом хорд найти положительный корень уравнения х4 - 2х – 4 = 0 с точностью до 0,01 Решение. Положительный корень будет находиться в промежутке (1; 1,7), т.к. f (1) = -5<0, а f (1,7) = 0,952>0. Найдем первое приближенное значение корня по формуле (3):
Получим Так как f (1,588) = -0,817 < 0, то применяя вторично способ хорд к промежутку (1,588; 1,7) получим: Найдем третье приближенное значение на промежутке (1,639; 1,7) получим: Найдем четвертое приближенное значение на отрезке (1,642; 1,7) получим: Следовательно, искомый корень с точностью до 0,01 равен 1,64 (до тех пор, пока значение в точке f(xi) по модулю не станет меньше заданной точности 0,01). §3. Метод касательных (Ньютона). Метод касательных –это метод отделения корней. Метод касательных отличается от метода хорд тем, что здесь рассматривается не секущая, соединяющая концы дуги графика, а касательная к графику. Точка пересечения касательной с осью ОХ дает приближенное значение корня. Пусть действительный корень уравнения f(x) = 0 изолирован на отрезке [a; b]. Выберем на отрезке [a; b] такое число х0, при котором
Проведем в точке М0 (х0; у = f(x). За приближенное значение корня примем абсциссу точки пересечения этой касательной с осью ОХ. Это приближенное значение корня найдется по формуле:
Применив этот метод вторично в точке М1 (х1;
и т.д. Полученная таким образом последовательность х0, х1, х2.... имеет своим пределом искомый корень. Пример 1.3: Методом касательных найти положительный корень уравнения х4 - 2х – 4 = 0 с точностью до 0,01 Решение. Здесь f(x) = х4 - 2х – 4, Так как f(x) и Тогда Применяя второй раз способ касательных, получим:
Аналогично получим третье приближение:
Следовательно, искомый корень с точностью до 0,01 равен 1,64
|
|||||
|
Последнее изменение этой страницы: 2016-12-27; просмотров: 1873; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.104.29 (0.005 с.) |
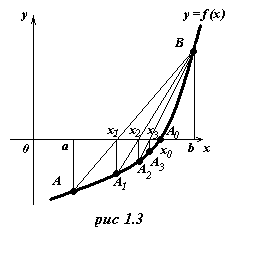 Метод хорд – это метод приближенного решения уравнения (1) имеет следующую геометрическую иллюстрацию: вместо точки пересечения оси ОХ и графика функции у = f(x), входящей в это уравнение, рассматривается точка пересечения данной оси и отрезка прямой, соединяющей концы дуги графика. Пусть требуется вычислить действительный корень уравнения f(x) = 0, изолированный на отрезке [a; b]. Рассмотрим график функции у = f(x). Пусть f (a) < 0, а f(b) > 0.
Метод хорд – это метод приближенного решения уравнения (1) имеет следующую геометрическую иллюстрацию: вместо точки пересечения оси ОХ и графика функции у = f(x), входящей в это уравнение, рассматривается точка пересечения данной оси и отрезка прямой, соединяющей концы дуги графика. Пусть требуется вычислить действительный корень уравнения f(x) = 0, изолированный на отрезке [a; b]. Рассмотрим график функции у = f(x). Пусть f (a) < 0, а f(b) > 0. (3)
(3) (4)
(4)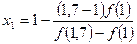 =1,588
=1,588 = 1,639; f (1,639) = -0,051 < 0.
= 1,639; f (1,639) = -0,051 < 0.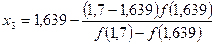 = 1,642; f (1,642) = -0,016 < 0.
= 1,642; f (1,642) = -0,016 < 0. = 1,643; f (1,643) =-0,004>0.
= 1,643; f (1,643) =-0,004>0.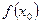 имеет тот же знак что и
имеет тот же знак что и  , т.е. выполняется условие
, т.е. выполняется условие 
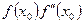 >0 (5)
>0 (5) (6)
(6) ), получим:
), получим: (7)
(7) =4х3 – 2,
=4х3 – 2,  = 12х2.
= 12х2.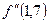 = 34,68> 0, то применяя формулу
= 34,68> 0, то применяя формулу  =17,652.
=17,652.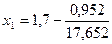 = 1,646.
= 1,646.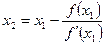 , где
, где  =
= 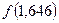 = 0,048,
= 0,048,  =15,838.
=15,838. 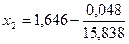 = 1,643.
= 1,643.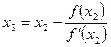 ,
,  =0,004,
=0,004,  =15,740, следовательно,
=15,740, следовательно,  = 1,6427.
= 1,6427.


