
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Составление структурно-математической схемы САУ
Структурно-математическая схемы системы автоматического регулирования температуры изображена на рис.3. В соответствии со структурно – математической схемой дифференциальное уравнение линейной части системы можно записать в следующем виде:
Подставим в уравнение (1.7) численные значения параметров и получим
Уравнение нелинейной части (1.7) дополняется уравнением нелинейного звена (1.3)
Раздел 2. Метод фазовых траекторий Исследуем устойчивость САУ температуры методом фазового пространства при отключенной местной обратной связи (см. рис.1). В режиме стабилизации температуры можно принять 1) Уравнение объекта регулирования
2) Уравнение чувствительного элемента
3) Уравнение усилителя (при kос=0)
4) Уравнение двигателя постоянного тока
5) Уравнение редуктора
Учитывая, что ток в обмотке поляризованного реле пропорционален отклонению температуры
Рис. 1. Статическая характеристика нелинейного звена
На этом рисунке
В соответствии с уравнением объекта регулирования (2.1) и статической характеристикой нелинейого звена (см.рис. 1) уравнения всей системы можно записать в следующем виде:
(2.7)
(2.8) (2.9) (2.10)
(2.11)
(2.12)
(2.13)
(2.14)
(2.15)
(2.16)
Подставив в уравнения (2.14) - (2.16) численные значения, получим:
По данным уравнениям построим фазовый портрет всей системы. Раздел 3. Метод Ляпунова
Согласно структурно-математической схеме САУ температуры описывается следующими дифференциальными и алгебраическими уравнениями:
(3.1)
Введем обозначения:
Получим:
Общий вид системы нелинейных уравнений 2-го порядка, заданных в нормальной форме, представлен ниже:
Откуда следует:
Запишем уравнения в канонической форме. Для этого из коэффициентов уравнения составим определитель.
Для нашего случая определитель имеет вид:
Определим корни характеристического уравнения
Ввиду того, что в характеристическом уравнении имеется один нулевой корень, канонические уравнения записываются в следующем виде:
Определим постоянные
где Dik(λ) обозначает алгебраическое дополнение элемента i - той строки и k- го столбца определителя D(λ).
По формуле (3.7) определим:
Определим D(λ):
Поскольку λ1=0, то и
Для класса нелинейных систем, к которому принадлежит рассматриваемая система, достаточные условия устойчивости имеют вид:
Это условие приводит к следующему достаточному условию устойчивости рассматриваемой системы:
|
|||||
|
Последнее изменение этой страницы: 2016-12-13; просмотров: 276; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.246.203 (0.008 с.) |
 (1.7)
(1.7) (1.8)
(1.8) (1.9)
(1.9) . При этом уравнения звеньев системы можно записать в следующем виде:
. При этом уравнения звеньев системы можно записать в следующем виде:

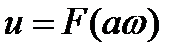


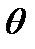 , а скорость отклонения регулирующего органа
, а скорость отклонения регулирующего органа  пропорциональна напряжению
пропорциональна напряжению  , в качестве входной величины нелинейного звена (поляризованного реле) можно принять
, в качестве входной величины нелинейного звена (поляризованного реле) можно принять 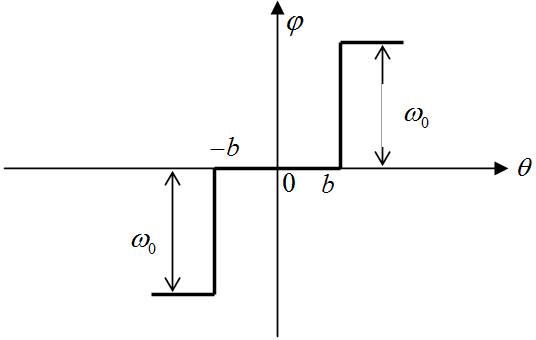
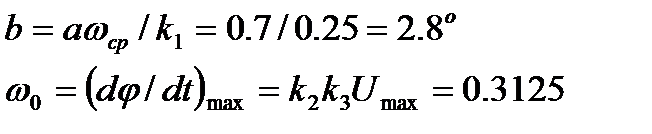
 (2.6)
(2.6)
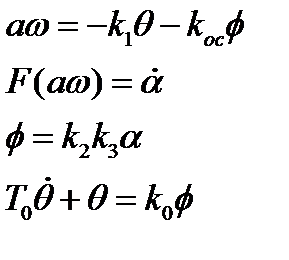

 (3.2)
(3.2) (3.3)
(3.3)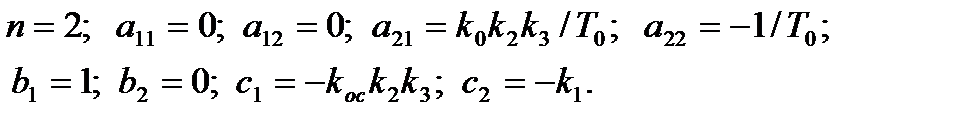
 (3.4)
(3.4) (3.5)
(3.5) (3.6)
(3.6) :
: (3.7)
(3.7)
 (3.8)
(3.8)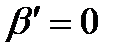
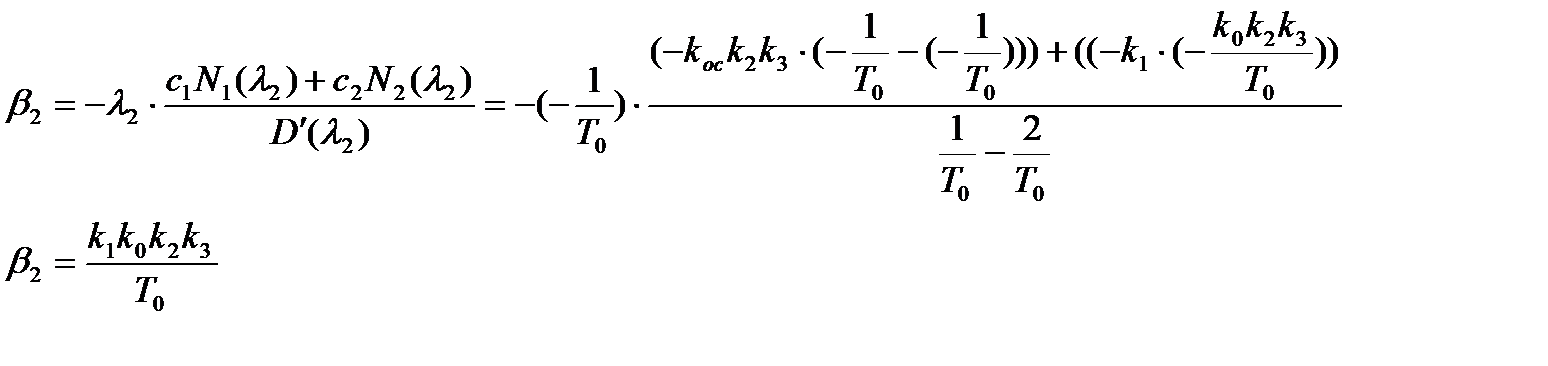 (3.9)
(3.9)




