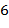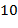Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Элементы теории чисел и общей алгебрыСтр 1 из 11Следующая ⇒
I. Введение I. 1. Предмет алгебры и теории чисел I.2. Основные понятия и обозначения из теории множеств математической логики Литература к разделу: 1. Кострикин А. И. Введение в алгебру.− М.: Наука, 1977. 2. Виноградов И. М. Основы теории чисел.− М.: Наука, 1965. II. Элементарная теория чисел Теория чисел занимается изучением свойств чисел. В данном разделе рассматриваются некоторые понятия и результаты классической теории чисел на основе арифметических свойств делимости и простых комбинаторных соображений без привлечения специальных понятий геометрии, алгебры и анализа, иррациональных и комплексных чисел. Замечание. Традиционно в теории чисел неэлементарными считаются доказательства, в которых используются мнимые числа. Геометрические, алгебраические, аналитические, вероятностные методы − предмет более продвинутого изучения. Далее используются обозначения: ℕ = {1, 2, 3, …} − множество натуральных чисел; ℤ = {0, II.1. Теория делимости в ℤ Число Натуральное число Теорема Евклида. Множество ℙ простых чисел бесконечно. Доказательство ( от противного ). Допустим, что множество ℙ конечно и состоит из чисел
Последнее равенство, однако, невозможно, так как делителями единицы в ℤ являются лишь 1 и −1. Значит, Теорема (о делении в ℤ с остатком). Для любых
Числа
Доказательство. Рассмотрим множество чисел
Так как
Для чисел Пусть числа Алгоритм Евклида вычисления нод 1) 2) 3) и осуществляется по схеме: a:=abs(a); b:=abs(b); while (a >0)&(b >0) do { if a>b then a:=a mod b else b:=b mod a}; нод:=a+b. Этот алгоритм затрачивает O Если Теорема. Пусть
в частности, если Доказательство. Положим
Выберем в
откуда следует, что число Наибольший общий делитель чисел нод ( Лемма. Пусть Доказательство. Допустим, что Основная теорема арифметики. Всякое натуральное число Доказательство. Факт представления числа
− два разложения числа В разложении числа на простые множители некоторые из них могут повторяться. Собирая одинаковые множители, получим
где Пример. Замечание. Доказать данную теорему, опираясь только на мультипликативные свойства (т.е. свойства умножения и деления) целых чисел невозможно. Необходимо привлечение аддитивных свойств (т.е. свойств сложения). Это можно проиллюстрировать на примере множества Наименьшее общее кратное чисел Теорема. Пусть
Доказательство. Пусть
II.2. Сравнения в ℤ Пусть
Запись Отметим следующие свойства сравнений:
(свойства
где символ
т.е. обе части сравнения можно разделить на любой общий делитель при условии, что этот делитель взаимно прост с модулем;
т.е. обе части сравнения и модуль можно разделить на любой их общий делитель;
Полная системам вычетов по модулю
Нетрудно установить, что
Другими словами, классы
Каждое число из класса
образует полную систему наименьших неотрицательных вычетов по модулю Теорема. Пусть Доказательство. Если Приведённая система вычетов по модулю В разбиении Теорема. Пусть нод ( Доказательство. Если Функция Эйлера Первые
Далее будет установлена формула для этой функции.
|
|||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-13; просмотров: 287; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.129.247.196 (0.076 с.) |
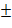 1,
1, 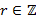 называется делителем числа
называется делителем числа 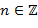 , если
, если  для некоторого
для некоторого  . В свою очередь
. В свою очередь 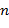 называется кратным числа
называется кратным числа  . Факт делимости обозначается как
. Факт делимости обозначается как 
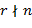 (читается:
(читается:  и
и  , то
, то 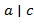 . Отметим также: если
. Отметим также: если 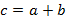 ,
,  и
и 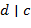 , то
, то  .
. называется простым, если все его натуральные делители исчерпываются числами
называется простым, если все его натуральные делители исчерпываются числами  и
и 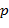 . Натуральное число
. Натуральное число  , не являющееся простым, называется составным. Число
, не являющееся простым, называется составным. Число  ,
,  ,…,
,…,  .Тогда число
.Тогда число  является составным и представимо в виде
является составным и представимо в виде  для некоторых
для некоторых  и
и 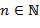 , и, следовательно,
, и, следовательно, .
. не может быть конечным множеством. ∎
не может быть конечным множеством. ∎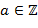 и
и  существуют единственные
существуют единственные 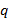 ,
,  ,
,  .
.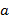 на
на 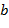 .
. ,
,  .
. , и
, и  , то
, то  (
(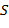 не пусто). Пусть
не пусто). Пусть  − наименьшее число в
− наименьшее число в  . Если допустить, что
. Если допустить, что  , то
, то 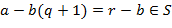 , а это противоречит выбору числа
, а это противоречит выбору числа  . Остаётся доказать, что числа
. Остаётся доказать, что числа  ,
, 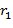 такие, что
такие, что  ,
, 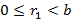 . Тогда
. Тогда  Для определённости, считаем, что
Для определённости, считаем, что  . Тогда
. Тогда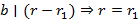 и
и 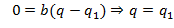 . ∎
. ∎ ,
, 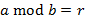 , где
, где 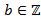 не равны нулю одновременно. Наибольшее
не равны нулю одновременно. Наибольшее 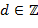 такое, что
такое, что 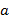 и
и 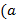 ,
, 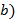 (или как нод
(или как нод 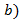 , если возникает коллизия обозначений с векторами).
, если возникает коллизия обозначений с векторами).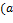 ,
, 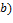 основан на использовании следующих свойств:
основан на использовании следующих свойств: ;
;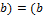 ,
,  ;
; ,
,  ,
,  времени (по числу арифметических операций). Анализ этого и других алгоритмов вычисления нодсм. у Д. Кнута (т. 2, § 4.5.2, 4.5.3).
времени (по числу арифметических операций). Анализ этого и других алгоритмов вычисления нодсм. у Д. Кнута (т. 2, § 4.5.2, 4.5.3). ,
,  , то числа
, то числа  и
и  называются взаимно простыми.
называются взаимно простыми.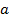 ,
,  ,
, 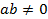 . Тогда существуют
. Тогда существуют 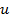 ,
,  такие, что
такие, что ;
;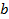 взаимно просты,
взаимно просты,  то для некоторых
то для некоторых 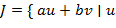 ,
,  }.
}. наименьшее положительное число
наименьшее положительное число  . Запишем число
. Запишем число 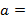
 , где
, где 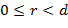 . Имеем
. Имеем 
 . Поскольку
. Поскольку , то
, то  (по условию выбора
(по условию выбора  ), и, следовательно,
), и, следовательно,  − любой общий делитель чисел
− любой общий делитель чисел 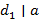 ,
,  ,
,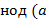 ,
, 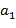 ,
,  , …,
, …,  может быть вычислен по схеме:
может быть вычислен по схеме: ,
,  ,
,  ,…,
,…,  , то либо
, то либо 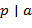 , либо
, либо 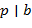 (либо и то, и другое).
(либо и то, и другое).  . Тогда
. Тогда  для некоторых
для некоторых  . Так как
. Так как  , то
, то  . ∎
. ∎ разлагается в произведение простых чисел, причем единственным способом, если не учитывать порядок сомножителей.
разлагается в произведение простых чисел, причем единственным способом, если не учитывать порядок сомножителей.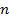 в виде произведения простых сомножителей очевиден. Докажем единственность такого представления. Пусть
в виде произведения простых сомножителей очевиден. Докажем единственность такого представления. Пусть
 на простые сомножители
на простые сомножители  ,
, 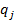 . Тогда из предыдущей леммы следует, что
. Тогда из предыдущей леммы следует, что  делит одно из чисел
делит одно из чисел  ,
,  , …,
, …,  . Пусть, для определённости
. Пусть, для определённости 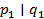 . Поскольку
. Поскольку 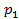 . Переходя к равенству
. Переходя к равенству 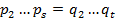 , получаем аналогично, что
, получаем аналогично, что  , и так далее. ∎
, и так далее. ∎ ,
, − различные простые числа,
− различные простые числа,  ,
,  , …,
, …,  . Такое преставление называется каноническим разложением числа на простые множители.
. Такое преставление называется каноническим разложением числа на простые множители. .
. , 4, 6,…} чётных чисел. Оно замкнуто относительно умножения:
, 4, 6,…} чётных чисел. Оно замкнуто относительно умножения:  ,
, 
 . Всякое число
. Всякое число  представимо в виде произведения чисел
представимо в виде произведения чисел  ,…,
,…, 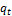 , каждое из которых неразложимо в
, каждое из которых неразложимо в  . Такие числа
. Такие числа  назовём
назовём  . Очевидно, что первая часть Основной теоремы выполняется. Однако вторая часть (об однозначности разложения) для
. Очевидно, что первая часть Основной теоремы выполняется. Однако вторая часть (об однозначности разложения) для 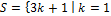 ,
, 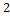 ,
,  ,…
,…  ,
,  такое, что
такое, что 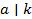 и
и  , и обозначается символом
, и обозначается символом  ,
,  (или нок
(или нок 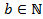 . Тогда
. Тогда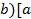 ,
, 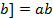 .
. и
и  − канонические разложения чисел
− канонические разложения чисел  ,
, 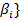 ,
,  ,
,  , …,
, …, 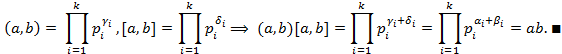
 называются сравнимыми по модулю
называются сравнимыми по модулю 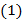
 .
. означает, что для чисел
означает, что для чисел  сравнение
сравнение 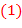 не имеет места.
не имеет места.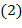
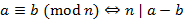 ;
;
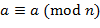 ;
;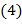

 ;
;
 и
и 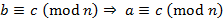
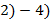 означают, что отношение сравнимости рефлексивно, симметрично и транзитивно, т.е. является отношением эквивалентности на множестве ℤ);
означают, что отношение сравнимости рефлексивно, симметрично и транзитивно, т.е. является отношением эквивалентности на множестве ℤ);
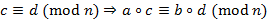 ,
, может быть заменён на любой из символов:
может быть заменён на любой из символов:  (сложение), − (вычитание) или ∙ (умножение), но на один и тот же в обеих частях сравнения, так что сравнения можно почленно складывать, вычитать и перемножать);
(сложение), − (вычитание) или ∙ (умножение), но на один и тот же в обеих частях сравнения, так что сравнения можно почленно складывать, вычитать и перемножать);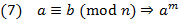 ≡
≡ 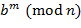 ,
,  ;
;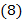 если
если 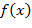 − многочлен с целочисленными коэффициентами, то
− многочлен с целочисленными коэффициентами, то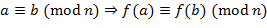 ;
;
 ;
; если
если  ,
, 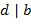 ,
,  ,
, 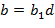 , нод
, нод  ,
,  , то
, то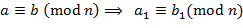 ,
,
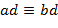 (mod
(mod  ),
),
 , где
, где  нок
нок  ,
,  ;
;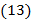
 ,
,  , и
, и 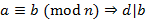 ;
;
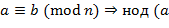 ,
, 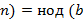 ,
,  .
. . Пусть
. Пусть  , включая в него все числа, сравнимые с
, включая в него все числа, сравнимые с 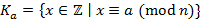 .
.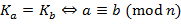 ,
,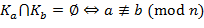 .
. ,
,  ,…,
,…, 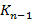 попарно не пересекаются, и любой класс
попарно не пересекаются, и любой класс  на непересекающиеся классы:
на непересекающиеся классы: .
. , 1, …,
, 1, …, 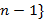
 ) = нод (
) = нод (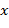 пробегает полную систему вычетов по модулю
пробегает полную систему вычетов по модулю  также пробегает полную систему вычетов по модулю
также пробегает полную систему вычетов по модулю  , то из свойств сравнений следует, что
, то из свойств сравнений следует, что  . Поэтому, если
. Поэтому, если  , то
, то  . ∎
. ∎ . Из оставшихся классов (для них нод
. Из оставшихся классов (для них нод  ) возьмём по одному вычету. В результате получим систему вычетов, которую называют приведённой системой вычетов по модулю
) возьмём по одному вычету. В результате получим систему вычетов, которую называют приведённой системой вычетов по модулю  также пробегает приведённую систему вычетов по модулю
также пробегает приведённую систему вычетов по модулю  , то
, то  (mod
(mod  . Остаётся учесть, что нод (
. Остаётся учесть, что нод (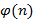 определяется как количество чисел среди
определяется как количество чисел среди  , …,
, …, 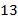 значений
значений