
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Еластичність функції. Попит на конкурентні товари
Поняття частинної похідної знаходить застосування в економічній теорії. Аналогічно до поняття еластичності функції однієї змінної вводиться поняття частинної еластичності функції декількох змінних
Розглянемо частинні похідні
Маємо Якщо розглядати попит Якщо при дослідженні попиту на даний товар розглядати вплив другого, альтернативного товару ціною Частинні похідні та диференціали першого порядку Частинні похідні
Нехай функція Означення. Величина
називається частинним приростом функції Аналогічно вводиться частинний приріст
Означення. Якщо існує границя
то вона називається частинною похідною першого порядку функції
Аналогічно частинна похідна першого порядку функції
і позначається одним із символів:
Згідно з означенням, при знаходженні частинної похідної ä Приклад. Знайти частинні похідні функції
ä Приклад. Потік пасажирів Похідна Диференційована функція Означення. Операція знаходження похідної Означення. Функція
можна представити у вигляді
де
Означення. Функція
Теорема 1. Якщо функція Теорема 2. Якщо функція
Теорема 3. Якщо функція
Повний диференціал функції Означення.Повним диференціалом
Повний диференціал
або
ä Приклад. Знайти повний приріст і повний диференціал функції
Оскільки то Повний приріст і повний диференціал функції в точці
Тоді різниця
|
||||||
|
Последнее изменение этой страницы: 2016-12-12; просмотров: 409; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.12.161.77 (0.017 с.) |
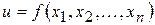 відносно змінної
відносно змінної  :
: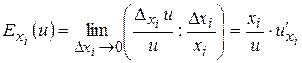 .
. і
і 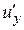 функції корисності. Вони називаються граничними корисностями
функції корисності. Вони називаються граничними корисностями 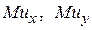 . Якщо вимірювати кількість товару у вартісному виразі, то граничні корисності можна розглядати як функції попиту на відповідний товар. Знайдемо граничні корисності для функції постійної еластичності
. Якщо вимірювати кількість товару у вартісному виразі, то граничні корисності можна розглядати як функції попиту на відповідний товар. Знайдемо граничні корисності для функції постійної еластичності .
.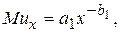
 тобто функції попиту з ростом вартості кожного товару є спадними, а параметри
тобто функції попиту з ростом вартості кожного товару є спадними, а параметри 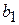 і
і  представляють частинні еластичності попиту на ці товари.
представляють частинні еластичності попиту на ці товари. як функцію декількох змінних, наприклад двох – ціни товару
як функцію декількох змінних, наприклад двох – ціни товару 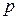 і доходів споживачів
і доходів споживачів  , тобто
, тобто  , то можна говорити про частинні еластичності попиту від ціни
, то можна говорити про частинні еластичності попиту від ціни  і попиту від доходів
і попиту від доходів 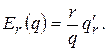 Наприклад, можна встановити, що
Наприклад, можна встановити, що  для якісних товарів і
для якісних товарів і 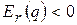 для товарів низького гатунку, так як з ростом доходів попит на якісні товари збільшується, а на товари низького гатунку – зменшується.
для товарів низького гатунку, так як з ростом доходів попит на якісні товари збільшується, а на товари низького гатунку – зменшується. , тобто розглядати попит як функцію трьох змінних
, тобто розглядати попит як функцію трьох змінних  , то можна ввести перехресний коефіцієнт еластичності попиту, який визначається за формулою
, то можна ввести перехресний коефіцієнт еластичності попиту, який визначається за формулою  і показує наближено відсоткову зміну попиту на даний товар при зміні ціни альтернативного товару на 1%. Очевидно, що для товарів, які взаємозамінюються
і показує наближено відсоткову зміну попиту на даний товар при зміні ціни альтернативного товару на 1%. Очевидно, що для товарів, які взаємозамінюються  , так як збільшення ціни одного товару призводить до збільшення попиту на інший. В той же час для взаємодоповнюючих товарів
, так як збільшення ціни одного товару призводить до збільшення попиту на інший. В той же час для взаємодоповнюючих товарів  , бо в цьому випадку ріст ціни будь-якого товару призводить до зниження попиту.
, бо в цьому випадку ріст ціни будь-якого товару призводить до зниження попиту. визначена в деякому околі точки
визначена в деякому околі точки  . Надамо змінній
. Надамо змінній  приросту
приросту  , залишаючи змінну
, залишаючи змінну 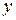 незмінною, так, щоб точка
незмінною, так, щоб точка  належала заданому околу.
належала заданому околу.
 по змінній х.
по змінній х. функції по змінній
функції по змінній  .
.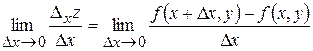 ,
, по змінній
по змінній  ;
; – частинні похідні по х в точці
– частинні похідні по х в точці 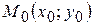 .
.
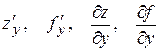 .
. обчислюють звичайну похідну функції однієї змінної х, вважаючи змінну
обчислюють звичайну похідну функції однієї змінної х, вважаючи змінну  сталою вважається змінна х.
сталою вважається змінна х. .
.

 виражається функцією
виражається функцією 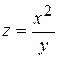 , де х – число мешканців,
, де х – число мешканців,  показує, що при одній і тій же відстані між містами збільшення потоку пасажирів пропорційне подвоєному числу мешканців. Похідна
показує, що при одній і тій же відстані між містами збільшення потоку пасажирів пропорційне подвоєному числу мешканців. Похідна 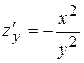 показує, що при одній і тій же чисельності мешканців збільшення потоку пасажирів обернено пропорційне квадрату відстані між містами.
показує, що при одній і тій же чисельності мешканців збільшення потоку пасажирів обернено пропорційне квадрату відстані між містами. – точкою диференціювання. Операція знаходження похідної
– точкою диференціювання. Операція знаходження похідної 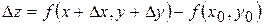
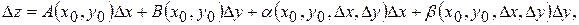
 – дійсні числа, а функції
– дійсні числа, а функції 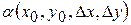 ,
,  такі, що
такі, що
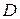 , якщо вона диференційована в кожній точці
, якщо вона диференційована в кожній точці  цієї області.
цієї області.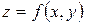 диференційована в точці
диференційована в точці 
 функції двох змінних
функції двох змінних 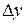 , тобто
, тобто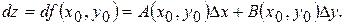
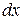 і
і  – диференціали незалежних змінних,
– диференціали незалежних змінних, 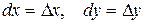 має вигляд:
має вигляд: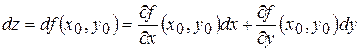
 .
.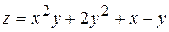 в точці
в точці  , якщо
, якщо 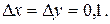
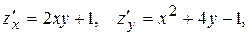
 а
а 
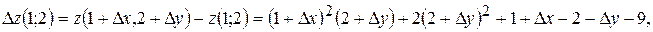

 являє собою похибку, яка виникає від заміни повного приросту
являє собою похибку, яка виникає від заміни повного приросту  функції її повним диференціалом
функції її повним диференціалом 





