
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Продольная сила. Напряжения и деформации
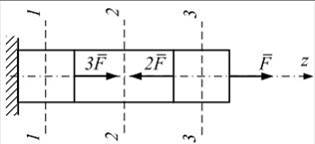
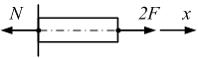
Задача 2.1.1: Для стержня, схема которого изображена на рисунке, продольная сила N в сечении 2-2 будет…
Варианты ответов: 1) равной нулю; 2) равномерно распределенной по сечению; 3) растягивающей; 4) сжимающей. Решение: 1), 3) Ответ неверный! Скорее всего, допущена ошибка при определении продольной силы. Условие равновесия для правой части стержня от сечения 2-2 −
2) Ответ неверный! Продольная сила – это равнодействующая нормальных напряжений, равномерно распределенных по площади поперечного сечения. Продольная сила – это сосредоточенная сила. 4) Ответ верный. Для определения продольной силы следует рассмотреть равновесие отсеченной правой части стержня
Задача 2.1.2: Сплошной однородный стержень круглого поперечного сечения диаметром d нагружен так, как показано на рисунке. Нормальные напряжения в сечении
Варианты ответов: 1) Решение: 1) Ответ неверный! Площадь круглого поперечного сечения равна 2) Ответ верный. Нормальные напряжения при растяжении − сжатии определяются по формуле
3) Ответ неверный! Неправильно определена продольная сила N. Продольная сила N находится из условия равновесия оставленной части: 4) Ответ неверный! Нормальные напряжения при растяжении − сжатии находят по формуле
Задача 2.1.3: Из гипотезы плоских сечений следует, что вдали от мест нагружения, резкого изменения формы и размеров поперечного сечения нормальные напряжения при растяжении − сжатии прямолинейных стержней распределяются по площади поперечного сечения … Варианты ответов: 1) по закону квадратной параболы, достигая максимума на нейтральной линии; 2) по линейному закону, достигая минимума на нейтральной линии; 3) неравномерно, в зависимости от формы поперечного сечения; 4) равномерно. Решение: 1), 2) Ответ неверный! Понятие «нейтральная линия» используется при изгибе. При растяжении − сжатии из гипотезы плоских сечений следует, что нормальные напряжения распределяются равномерно по площади поперечного сечения стержня.
3) Ответ неверный! Из гипотезы плоских сечений следует, что нормальные напряжения при растяжении − сжатии распределяются равномерно по площади поперечного сечения стержня. От формы поперечного сечения напряжения в данном случае не зависят. 4) Ответ верный. Гипотеза плоских сечений (Я. Бернули, 1654 − 1705) гласит: поперечные сечения стержня, плоские и нормальные до деформации к его оси, остаются плоскими и нормальными к оси и после деформации. Из гипотезы следует, что нормальные напряжения при растяжении − сжатии распределяются равномерно по площади поперечного сечения стержня.
Задача 2.1.4: Распределение нормальных напряжений при растяжении − сжатии вдали от мест нагружения, резкого изменения формы и размеров поперечного сечения существенно зависит от… Варианты ответов: 1) величины и способа приложения внешних сил; 2) величины приложенных внешних сил; 3) способа приложения внешних сил; 4) от формы поперечного сечения Решение: 1), 3) Ответ неверный! Согласно принципу Сен-Венана на достаточном удалении от места нагружения распределение напряжений зависит только от статического эквивалента приложенных внешних сил. От способа приложения внешних сил распределение напряжений зависит существенно лишь вблизи места нагружения. 2) Ответ верный. Согласно принципу Сен-Венана, если тело нагружается статически эквивалентными системами сил и размеры области их приложения невелики (по сравнению с размерами тела), то в сечениях, достаточно удаленных от мест приложения нагрузок, величина напряжений весьма мало зависит от способа нагружения.
4) Ответ неверный! Нормальные напряжения при растяжении-сжатии определяются по формуле
Задача 2.1.5: Для стержня круглого поперечного сечения, схема которого изображена на рисунке, абсолютное удлинение
Варианты ответов: 1) Решение: 1) Ответ верный.
2) Ответ неверный! Напомним, что удлинение стержня в случае, когда 3), 4) Ответ неверный! Скорее всего, допущена ошибка при определении продольной силы. Условие равновесия
Задача 2.1.6: Стержень нагружен системой сил. Модуль упругости материала Е, площадь поперечного сечения А, размер а, значение силы F заданы. Продольная линейная деформация на участке СК равна …
1) Решение: 1) Ответ верный. Сделаем произвольное поперечное сечение на участке СК и рассмотрим равновесие правой отсеченной части. 2) Ответ неверный! При определении продольной линейной деформации 3), 4) Ответ неверный! Неправильно определена величина продольной силы.
|
||||||
|
Последнее изменение этой страницы: 2016-12-10; просмотров: 3962; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.223.172.252 (0.013 с.) |
 ,
,  ,
, 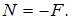
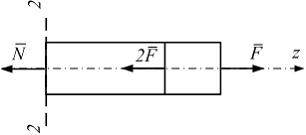
 откуда
откуда 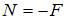 . В сечении 2-2 действует сжимающая продольная сила.
. В сечении 2-2 действует сжимающая продольная сила.
 равны…
равны…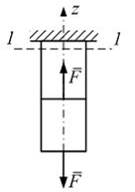
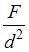 ; 2) 0; 3)
; 2) 0; 3)  ; 4)
; 4) 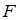 .
.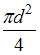 , где d – диаметр круга. Условие равновесия имеет вид
, где d – диаметр круга. Условие равновесия имеет вид 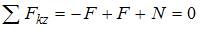 .
.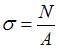 . Продольная сила N определяется из условия равновесия для отсеченной части стержня
. Продольная сила N определяется из условия равновесия для отсеченной части стержня 
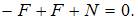 Откуда
Откуда  В результате
В результате  .
.
 , откуда
, откуда 
 . Здесь N − продольная сила; А − площадь поперечного сечения стержня. Таким образом, нормальные напряжения при растяжении − сжатии от формы поперечного сечения не зависят.
. Здесь N − продольная сила; А − площадь поперечного сечения стержня. Таким образом, нормальные напряжения при растяжении − сжатии от формы поперечного сечения не зависят.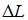 равно…
равно…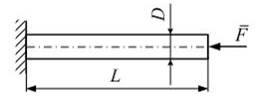
 ; 2)
; 2)  ; 3)
; 3)  ; 4) 0
; 4) 0
 В нашем случае
В нашем случае  ,
, 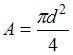 . Окончательно
. Окончательно  .
.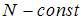 и
и 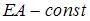 , находится по формуле
, находится по формуле 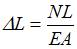 . Здесь
. Здесь 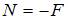 и
и 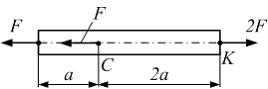
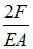 ; 2)
; 2) 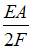 ; 3)
; 3) 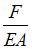 ; 4)
; 4)  .
.
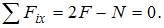
 Далее определяем нормальное напряжение:
Далее определяем нормальное напряжение:  Из закона Гука
Из закона Гука 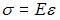 вычислим значение продольной линейной деформации:
вычислим значение продольной линейной деформации: 
 .
.

 .
. .
.


