
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 16 Числовые характеристики случайных величин
Лекция 3.16.1 «Числовые характеристики случайных величин» Учебные вопросы: 1. Характеристики положения 2. Характеристики рассеивания
Характеристики положения Случайные величины, помимо законов распределения, могут также описываться числовыми характеристиками, среди которых различают характеристики положения (математическое ожидание, мода, медиана и др.) и характеристики рассеивания (дисперсия, среднеквадратичное отклонение, различные моменты распределения порядка выше первого и др.). Математическим ожиданием (средним значением по распределению, средним) называется действительное число, определяемое в зависимости от типа случайной величины X формулой
Из определения математического ожидания легко получаются следующие его свойства: a. Аддитивность b. Для любого числа
т. е. постоянный множитель c. Математическое ожидание индикатора
d. Свойство монотонности: если Х ≥ Y, то
e. Для независимых случайных величин X и Y имеет место мультипликативное свойство математического ожидания:
т. е. математическое ожидание произведения независимых случайных величин равно произведениюих математических ожиданий. Свойство мультипликативности распространяется на случай произвольного конечного числа независимых случайных величин. Следует отметить, что если свойство аддитивности математического ожидания справедливо для любых случайных величин, то свойство мультипликативности математического ожидания справедливо только для независимых случайных величин. Модой случайной величины X непрерывного типа называется такое ее числовое значение
k Таким образом, мода дискретной случайной величины есть ее наиболее вероятное значение в случае, если такое значение единственно. Мода может не существовать, иметь единственное значение (унимодальное распределение) или иметь множество значений (мультимодальноераспределение).
Медианой случайной величины X непрерывного типа называется такое ее числовое значение
Так как данное уравнение может иметь множество корней, то медиана определяется, вообще говоря, неоднозначно.
Характеристики рассеивания Дисперсией случайной величины X называется неотрицательное число
Неотрицательное число Свойства дисперсии: a. Дисперсия любой случайной величины b. Если
c. Если случайные величины X и Y независимы, то
Случайная величина X называется центрированной (обозначается mX = 0 и Начальным моментом m -го порядка(
Центральным моментом m -го порядка распределения случайной величины X называется число
Из определений моментов, в частности, следует, что a0 = Отметим еще две важные характеристики распределения, связанные с моментами высшего порядка: · коэффициент асимметрии или «скошенности» распределения
· коэффициент эксцесса или «островершинности» распределения
Квантилью порядка
В частности, из определения медианы следует, что hX =
|
||||||
|
Последнее изменение этой страницы: 2016-12-10; просмотров: 276; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.42.196 (0.01 с.) |
 (1)
(1) [ X + Y ] =
[ X + Y ] = 
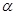 X ] =
X ] =  события А равно вероятности этого события:
события А равно вероятности этого события: (А);
(А); , для которого плотность распределения вероятностей
, для которого плотность распределения вероятностей  этой величины имеет максимум. Мода случайной величины дискретного типа определяется как такое ее возможное значение
этой величины имеет максимум. Мода случайной величины дискретного типа определяется как такое ее возможное значение  , для которого
, для которого , при котором
, при котором . (3)
. (3) [ Х ]
[ Х ]  , определяемое формулой
, определяемое формулой (4)
(4)
 называется среднеквадратичным отклонением (сокращенно с. к. о.) случайной величины X. Оно имеет размерность случайной величины X и определяет некоторый стандартный среднеквадратичный интервал рассеивания, симметричный относительно математического ожидания. (Величину
называется среднеквадратичным отклонением (сокращенно с. к. о.) случайной величины X. Оно имеет размерность случайной величины X и определяет некоторый стандартный среднеквадратичный интервал рассеивания, симметричный относительно математического ожидания. (Величину 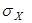 иногда называют стандартным отклонением.) Если величина X =const (т. е. X не случайна), то
иногда называют стандартным отклонением.) Если величина X =const (т. е. X не случайна), то  ] = 0.
] = 0.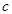 – постоянная, то
– постоянная, то ] =
] = 
 ] =
] = 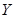 ].
]. ), если mX = 0. Случайная величина X называется стандартизованной, если
), если mX = 0. Случайная величина X называется стандартизованной, если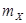 , а единицей измерения величины является
, а единицей измерения величины является 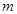 = 0, 1, 2,...) распределенияслучайной величины X называется действительное число
= 0, 1, 2,...) распределенияслучайной величины X называется действительное число  , определяемое по формуле
, определяемое по формуле (5)
(5)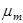 , определяемое по формуле
, определяемое по формуле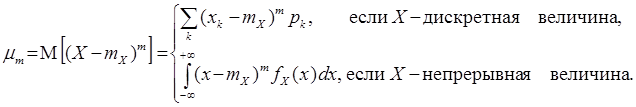 (6)
(6) = 1, mX = a1 , DХ =
= 1, mX = a1 , DХ =  =
=  = a2 -
= a2 - 
 , (7)
, (7)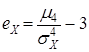 . (8)
. (8) распределения случайной величины X непрерывного типа называется действительное число
распределения случайной величины X непрерывного типа называется действительное число  , удовлетворяющее уравнению
, удовлетворяющее уравнению .
.


