
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Спектральна щільність та її властивості
Спектральним розкладом випадкового процесу називається зображення його у вигляді нескінченної суми гармонічних коливань різних частот з випадковими амплітудами і випадковими фазами. Спектром процесу називається функція, яка описує розподіл амплітуд за різними частотами. Спектр показує, які гармонічні складові переважають у процесі, яка його внутрішня структура. Спектральний розклад стаціонарного випадкового процесу X (t) в проміжку [0, T ], якщо відома його кореляційна функція kx (t) = Kx (t 1, t 2), де t = t 2 – t 1, має вигляд(оскільки кореляційна функція парна, то вона розкладається в проміжку [– T; T ] у ряд Фур’є за косинусами):
де w k = k w1,
D 0, D 1, …, Dk, … є невід’ємними величинами.
Канонічний розклад кореляційної функції стаціонарного випадкового процесу має вигляд:
Координатними функціями цього розкладу є косинуси і синуси частот, кратних w1: cos w kt, sin w kt (w k = k w1, k = 0, 1, 2, …).
Канонічний розклад випадкового процесу X(t) з тими ж координатними функціями має вигляд:
де Ak i Bk – некорельовані випадкові величини, що мають нульові математичні сподівання і попарно рівні додатні дисперсії
Канонічний розклад (2.4) називається спектральним розкладом стаціонарного випадкового процесу X(t) в проміжку [0, T]. Дисперсія цього стаціонарного випадкового процесу X (t) дорівнює
Розподіл дисперсій за частотами можна зобразити у вигляді спектра дисперсій (рис. 1), який називається також спектром стаціонарного випадкового процесу на скінченному проміжку. Сума всіх ординат спектра дисперсій дорівнює дисперсії стаціонарного випадкового процесу. Такий спектр називається лінійчастим.
Розглянемо спектральний розклад стаціонарного випадкового процесу на нескінченному інтервалі часу (T ® ¥), коли коефіцієнти розкладу (2.3) кореляційної функції будуть необмежено зменшуватись (Dk ® 0), а їх число в сумі (2.5) буде необмежено збільшуватись. При цьому величина
Введемо позначення
або,
Функція Sx (w) називається спектральною щільністю стаціонарного випадкового процесу X (t).
Площа, обмежена кривою Sx (w) і віссю абсцис чисельно дорівнює дисперсії Dx (t) цього процесу, тобто
Фізичний зміст спектральної щільності Sx (w): Якщо випадковий процес X (t) – це флуктуації електричного струму чи напруги, то спектральна щільність характеризує щільність потужності, яка припадає на одиницю частоти w.
Щільність потужності Sx (w) виражає собою частотний спектр даного випадкового процесу. Такий спектр називається енергетичним, оскільки мова йде про те, як розподілена енергія (середня потужність) процесу по частотному діапазону. Цей спектр дає усереднену картину розподілу енергії за частотами елементарних гармонічних складових.
Зв’язок між спектральною щільністю Sx (w) і кореляційною функцією kx (t) стаціонарного випадкового процесу.
Застосовуючи формули Ейлера eiz = cos z + i sin z, e – iz = cos z – i sin z співвідношення (2.9) можна записати в комплексній формі так:
Ці формули визначають пряме та обернене перетворення Фур’є і є узагальненням розкладу неперіодичної функції на гармонічні коливання в нескінченному інтервалі.
Означення. Якщо основна частина потужності концентрується в деякій вузькій смузі частот навколо фіксованої частоти w0, то такий випадковий процес називається вузькосмужним; якщо ж вказана умова не виконується, то процес- широкосмужний. Означення. Білим шумом називається стаціонарний процес з нульовим математичним сподіванням і сталою спектральною щільністю для всіх частот від 0 до ¥, тобто
mx (t) = 0, Sx (w) = S0 = const. (2.11)
Число S0 називається інтенсивністю білого шуму. Потужність білого шуму розподілена рівномірно по всьому діапазону частот. Для дисперсії білого шуму одержимо
Білий шум має нескінченну дисперсію, з ним пов’язана нескінченна енергія, тому фізично реалізувати білий шум неможливо. Його застосовують як математичну модель: кожний стаціонарний випадковий процес можна вважати білим шумом, якщо його спектральна щільність є сталою в межах смуги пропускання.
Контрольні запитання
1. Що називається спектральним розкладом випадкового процесу? 2. За якими функціями розкладається в ряд Фур’є кореляційна функція стаціонарного процесу? 3. Яку властивість мають коефіцієнти розкладу в ряд Фур’є кореляційної функції стаціонарного процесу? 4. Які функції є координатними функціями канонічного розкладу в ряд Фур’є кореляційної функції стаціонарного процесу? 5. Які властивості мають коефіцієнти канонічного розкладу в ряд Фур’є стаціонарного випадкового процесу? 6. Чому дорівнює сума дисперсій всіх гармонік спектрального розкладу стаціонарного процесу? 7. У чому фізичний зміст спектральної щільності стаціонарного процесу? 8. Який зв’язок між спектральною щільністю Sx (w) і кореляційною функцією kx (t) стаціонарного випадкового процесу? 9. Який процес називається білим шумом?
Розв’язування задач Задача №1 Знайти спектральну щільність телеграфного сигналу.
Розв’язання
Кореляційна функція телеграфного сигналу має вигляд:
Скористаємося формулою (4.12). Маємо:
Задача №2 Знайти спектральну щільність процесу з кореляційною функцією Розв’язання Замінивши
При обчисленні інтегралів використані результати попередньої задачі. Задача № 3 Кореляційна функція має вигляд Розв’язання Обчислюємо спектральну щільність аналогічно задачі 1:
Задача №4 Задано спектральну щільність процесу Розв’язання Порівнюючи спектральну функцію kx (t) = h 2 e – 2l| t | параметри, прийдемо до такої функції:
Практичне заняття 15 ЛІНІЙНІ ПЕРЕТВОРЕННЯ ВИПАДКОВИХ ПРОЦЕСІВ
На вхід деякої системи S подається випадковий процес X (t) – “ вхідний сигнал ”. Система S здійснює перетворення вхідного сигналу X (t), у результаті чого на виході системи маємо випадковий процес Y (t), який називається вихідним сигналом або реакцією системи S.
Це перетворення символічно запишемо у вигляді:
Y (t) = At { X (t)}, (3.1)
де At – оператор системи S. Індекс t означає, що оператор At здійснює перетворення випадкового процесу по аргументу t, який має, як правило, зміст часу. Розрізняють лінійні та нелінійні оператори. Лінійні оператори в свою чергу поділяють на однорідні та неоднорідні.
Оператор L називається лінійним однорідним оператором, якщо він має такі дві властивості: 1) L { X 1(t) + X 2(t)} = L { X 1(t)} + L { X 2(t)}; (3.2) 2) L { CX (t)} = CL { X (t)} (C = const).
Оператор L називається лінійним неоднорідним, якщо він складається з лінійного однорідного оператора L 0 з додаванням деякої цілком визначеної невипадкової функції j(t): L { X (t)} = L 0{ X (t)} + j(t). (3.3)
Оператори, які не є лінійними (однорідними чи неоднорідними), називаються нелінійними. Лінійними однорідними операторами є:
1) оператор множення на невипадкову функцію f (t):
Y (t) = L { X (t)} = f (t)· X (t); (3.4)
2) оператор диференціювання:
3) оператор інтегрування:
Лінійними неоднорідними операторами є:
1)Y (t) = L { X (t)} = f (t) X (t) + j(t), 2) 3) де f (t), j(t) – деякі невипадкові функції. Розглянемо кілька прикладів розв’язання задачі визначення характеристик реакції Y (t) лінійної системи, якщо відомі характеристики вхідного сигналу X (t).
Зауваження 1. Якщо відомі математичне сподівання mx (t) і кореляційна функція Kx (t 1, t 2) випадкового процесу X (t), то відповідні характеристики випадкового процесу
обчислюється за формулами:
Контрольні запитання
1. Що називається вхідним та вихідним сигналом? 2. Пояснити, що називається оператором системи. 3. Які оператори називаються лінійними однорідними? 4. Які оператори називаються лінійними неоднорідними? 5. Навести приклади лінійних однорідних операторів. 6. Навести приклади лінійних неоднорідних операторів.
Розв’язування задач
Задача№1
Відомі характеристики випадкового процесу X (t): mx (t) і Kx (t 1, t 2). Потрібно знайти математичне сподівання і кореляційну функцію випадкового процесу Y (t) = f (t)· X (t), де f (t) – невипадкова функція.
Розв’язання
Враховуючи, що f (t) – невипадкова функція, одержимо
my (t) = M (Y (t)) = M (f (t)· X (t)) = f (t) M (X (t)) = f (t)· mx (t).
Щоб знайти кореляційну функцію випадкового процесу Y (t), достатньо скористатись властивістю 6 кореляційної функції
Ky (t 1, t 2) = f (t 1) f (t 2) Kx (t 1, t 2).
Якщо, зокрема, f (t) = C = const, тобто Y (t) = CX (t), то my (t) = Cmx (t), Ky (t 1, t 2) = C 2 Kx (t 1, t 2).
Задача №2
Для випадкових процесів X (t), Y (t) відомі їхні математичні сподівання mx (t), my (t), кореляційні функції Kx (t 1, t 2), Ky (t 1, t 2) та взаємна кореляційна функція Kxy (t 1, t 2). Потрібно знайти математичне сподівання та кореляційну функцію випадкового процесу Z (t) = X (t) + Y (t). Розв’язання Використовуючи властивості математичного сподівання і означення кореляційної функції випадкового процесу, легко одержати такі вирази:
mz (t) = mx (t) + my (t),
Kz (t 1, t 2) = Kx (t 1, t 2) + Ky (t 1, t 2) + Kxy (t 1, t 2) + Kyx (t 1, t 2).
Якщо випадкові процеси X (t) та Y (t) некорельовані, то
Kxy (t 1, t 2) = Kyx (t 1, t 2) = 0 і кореляційна функція випадкового процесу Z (t) матиме вигляд
Kz (t 1, t 2) = Kx (t 1, t 2) + Ky (t 1, t 2).
Задача№3 Випадковий процес X (t) має характеристики
Розв’язання
Випадковий процес Y (t) є результатом диференціювання і множення на невипадкову функцію з додаванням невипадкової функції, застосованих до випадкового процесу X (t). Тому за формулами одержимо
Кореляційну функцію Ky (t 1, t 2) знаходимо за допомогою формул:
Крім того,
Задача№4 На вхід інтегруючої системи з оператором mx (t) = 3 t 2 – 8 t + 5, Kx (t 1, t 2) = cos w t 1 cos w t 2. Знайти характеристики випадкового процесу Y (t) на виході системи.
Розв’язання Скористаємося формулами. Маємо:
Звідси
Задача№5 Нехай стаціонарний випадковий процес X (t) має математичне сподівання mx (t) = mx = const і кореляційну функцію kx (t). Нехай
Розв’язування Нехай
Позначимо t = t 1 – t 2, тоді
Знайдемо тепер спектральну щільність випадкового процесу Y (t).
Задача№6
Нехай Z (t) = X (t) + Y (t) є сумою двох стаціонарних випадкових процесів X (t) та Y (t). Відомі характеристики процесів X (t) і Y (t): mx, kx (t), my, ky (t), а також їхня взаємна кореляційна функція Kxy (t 1, t 2) = Kyx (t 2, t 1). Знайти характеристики випадкового процесу Z (t).
Розв’язування Враховуючи результати задачі 2, одержимо
mz (t) = mx + my = mz = const;
Kz (t 1, t 2) = kx (t 1 – t 2) + ky (t 1 – t 2) + Kxy (t 1, t 2) + Kyx (t 1, t 2);
Dz (t) = kx (0) + ky (0) + 2 Kxy (t, t) = Dx + Dy + 2 Kxy (t, t).
Отже, математичне сподівання суми двох стаціонарних випадкових процесів є стала величина, а кореляційна функція є функцією двох аргументів t 1 і t 2. Тому в загальному випадку сума двох стаціонарних випадкових процесів не є стаціонарним випадковим процесом.
Задача№7
Нехай в умовах попередньої задачі відомо, що стаціонарні процеси X (t), Y (t) некорельовані. Чи буде сумарний процес стаціонарним?
Розв’язування Якщо процеси некорельовані, то Kxy (t 1, t 2) = 0. Звідки випливає, що Kz (t 1, t 2) = kx (t) + ky (t), тобто випадковий процес Z (t) є стаціонарним.
Задача№8 Лінійне однорідне перетворення – інтегрування стаціонарного випадкового процесу X (t):
Чи буде вихідний процес стаціонарним?
Розв’язування Лінійне однорідне перетворення – інтегрування стаціонарного випадкового процесу X (t)
приводить до нестаціонарного випадкового процесу, оскільки математичне сподівання випадкового процесу Y (t)
не є сталою величиною. Практичне заняття 16
|
||||||||
|
Последнее изменение этой страницы: 2016-12-10; просмотров: 636; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.8.42 (0.159 с.) |
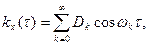 (2.1)
(2.1) , а коефіцієнти Dk ряду Фур’є визначаються за формулами:
, а коефіцієнти Dk ряду Фур’є визначаються за формулами: ,
, 
 . (2.2)
. (2.2) (2.3)
(2.3) (2.4)
(2.4) (2.5)
(2.5) Дисперсія стаціонарного випадкового процесу, зображеного канонічним розкладом (2.4), дорівнює сумі дисперсій всіх гармонік його спектрального розкладу.
Дисперсія стаціонарного випадкового процесу, зображеного канонічним розкладом (2.4), дорівнює сумі дисперсій всіх гармонік його спектрального розкладу. – інтервал між сусідніми частотами – також буде прямувати до нуля.
– інтервал між сусідніми частотами – також буде прямувати до нуля. , (2.6)
, (2.6) (2.7)
(2.7) . (2.8)
. (2.8)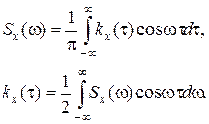 (2.9)
(2.9) (2.10)
(2.10)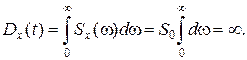 (2.12)
(2.12)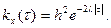

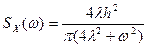 .
.
 на
на  , отримаємо:
, отримаємо:
 .
. ,
, 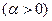 . Знайти спектральну щільність процесу.
. Знайти спектральну щільність процесу.

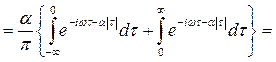
 .
.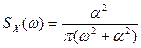 . Знайти кореляційну функцію.
. Знайти кореляційну функцію. переходять одна в одну. Тому і кореляційні функції повинні переходити одна в одну при такій заміні, тобто замінивши у формулі:
переходять одна в одну. Тому і кореляційні функції повинні переходити одна в одну при такій заміні, тобто замінивши у формулі: .
. ; (3.5)
; (3.5) . (3.6)
. (3.6)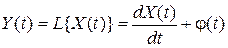 , (3.7)
, (3.7) ,
, мають вигляд:
мають вигляд: . Зауваження 2. Якщо відомі характеристики mx (t) і Kx (t 1, t 2) випадкового процесу X (t), то математичне сподівання my (t) і кореляційна функція Ky (t 1, t 2) випадкового процесу
. Зауваження 2. Якщо відомі характеристики mx (t) і Kx (t 1, t 2) випадкового процесу X (t), то математичне сподівання my (t) і кореляційна функція Ky (t 1, t 2) випадкового процесу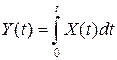
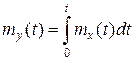 ,
,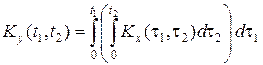 .
. . Знайти характеристики випадкового процесу
. Знайти характеристики випадкового процесу .
. .
. .
. .
. ;
;
 .
. . Далі за другою з формул маємо
. Далі за другою з формул маємо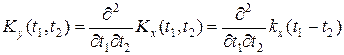 .
. .
.
 .
.



