
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение отношения теплоемкостей
Основные понятия и определения: уравнение Клапейрона-Менделеева, первое начало термодинамики, внутренняя энергия идеального газа, теплоемкость и виды теплоемкостей. Цель работы: научиться работать с электроприборами, измерять скорость звука по резонансу в воздушном столбе. Краткая теория Теплоемкость газов При термодинамическом равновесии состояние газа в целом может характеризоваться тремя параметрами: давлением P, объемом V и температурой Т. Соотношение, связывающее между собой эти величины, называется уравнением состояния газа. Для идеального газа таковым является уравнение Клапейрона - Менделеева, которое для данной массы газа m имеет вид:
где m - молярная масса газа, R- универсальная газовая постоянная. При равновесном переходе газа из одного состояния в другое, т.е. при термодинамическом процессе, должно выполниться первое начало термодинамики, которое можно сформулировать следующим образом: количество теплоты dQ, переданное газу, идет на изменение его внутренней энергии dU и на работу dA, совершаемую газом против внешних сил: dQ = dU + dA Элементарная работа dA=pdV, а внутренняя энергия одного киломоля идеального газа определяется по формуле
где i - число степеней свободы молекулы газа, Для одноатомных молекул i =3 (только 3 поступательных степени свободы); для двухатомных i =5 (3 поступательных и 2 вращательных); для трех и более атомных i =6 (3 поступательных и 3 вращательных). Теплоёмкостью С называется величина, равная отношению сообщенного телу при нагревании количества теплоты dQ к вызванному этим процессом изменению температуры dT:
Различают удельную теплоемкость Cуд – теплоёмкость одного килограмма газа в молярную Сm - теплоёмкость одного киломоля газа. Эти теплоёмкости связаны между собой равенством:
Теплоемкости для одного и того же газа не являются постоянными величинами, а зависят от характера процесса, при котором происходит нагревание газа, т.к. одному и тому же изменению температуры dT могут соответствовать различные значения работы dA. Рассмотрим основные изопроцессы, протекающие в одном киломоле идеального газа и найдем соответствующие им теплоёмкости. а) Изохорический процесс (V = const)
В этом случае dV=0, следовательно dA=0, и всё подводимое к газу количество теплоты идет на увеличение его внутренней энергии dU: dQ = dU. Тогда молярная теплоемкость при постоянном объёме, учитывая (I), равна:
б) Изобарический процесс (p = const) В этом случае молярная теплоемкость
Из уравнения состояния газа для одного киломоля имеем:
Т.к, p = const,то dp =0 и pdV=RdT. (4а) Подставляя (4а) в (3) и заменяя dU согласно (2) на
в) Изотермический процесс (T = const) В этом случае dT =0 и dQ = dA,т.е. все подводимое количество теплоты идет на совершение газом работы, а его внутренняя энергия остается постоянной. Т.к. температура при этом не изменяется, то молярная теплоёмкость равна Элементарная работа при изотермическом процессе определяется уравнением
Полная работа
где V1 и V2 - начальный и конечный объем газа при изотермическом расширении Из уравнения Клапейрона- Менделеева для любой массы газа
Находим давление Тогда Данный интеграл имеет следующее решение
Итак, работа газа при изотермическом расширении определяется уравнением
г) Адиабатический процесс (dQ = 0, dU + dA = 0) – процесс, происходящий при отсутствии теплообмена между газом и окружающей средой. Т.к. при этом dQ =0,то молярная теплоёмкость равна нулю. Выведем уравнение адиабатического процесса (уравнение Пуассона). dA = -dU или pdV = -CvdT. (6)
Разделив равенство (4) на (6), учитывая (5),получим:
где Если вместо Ср и Сv подставить в выражение для g их значения через число степеней свободы идеального газа i, то получим:
Интегрируя и потенцируя уравнение (7), получим уравнение Пуассона:
В данной работе определяется отношение g для воздуха по скорости звука в нем. Теория метода Звуковые волны в газах являются продольными и представляют собой последовательные сжатия и разрежения частиц газа. Скорость распространения звуковой волны зависит от упругости газа и его плотности:
где Е – модуль упругости (Юнга). Модуль упругости Е, по определению, есть коэффициент пропорциональности между относительным удлинением тела
В продольной волне при одностороннем растяжении относительное удлинение
При распространении волн в газовой среде вследствие сжатий и разрежений происходит изменение температуры различных участков. Причём опыт показал, что для звуковых волн за время одного колебания температура между сжатыми (и тем самым разогретыми) и разреженными (и тем самым охлаждёнными) областями волны не успевает выравниваться. Поэтому кратковременные процессы сжатия и разрежения можно считать происходящими без теплообмена, т.е. адиабатическими. Дифференцируя уравнение Пуассона (9), получим:
Подставляя выражение (12) в равенство (11), для модуля упругости получим:
Плотность раза r можно получить из уравнения Клайперона- Менделеева:
Подставляя (13) и (14) в (10), получим
Таким образом, для определения показателя адиабаты достаточно измерить абсолютную температуру газа и скорость распространения звука в нем (молярная масса газа считается известной). В вашей работе газом является воздух и его молярная масса m = 29 кг/кмоль. Скорость же звука u измеряется с помощью установки, изображенной на рис. 1. Звуковые колебания возбуждаются в трубе Т телефоном Тф, укрепленным на конце подвижного поршня П, а улавливаются микрофоном М у открытого конца трубы. Телефон подключается к звуковому генератору ЗГ, а возникающие в микрофоне электрические сигналы наблюдаются на экране осциллографа Э0. Колебаний мембраны телефона приведут в движение частицы воздуха, прилегающие к ней, которые в свою очередь приведут в движение находящиеся за ними соседние частицы и т.д., то есть в трубе будет распространяться звуковая волна. Эта волна будет испытывать многократные отражения от закрытого и открытого концов трубы, поэтому звуковые колебания в результате наложения на первоначальную волну всех отраженных волн, вообще говоря, имеют сложный вид. Картина значительно упрощается, если в трубе возникает акустический резонанс, которому соответствует резкое увеличение амплитуды электрических колебаний, наблюдаемых на экране осциллографа.
Рисунок 1. Установка, для измерения скорости звука в воздухе
Резонанс - это явление резкого возрастания амплитуды вынужденных колебаний и колебательной системе при приближении частоты вынуждающей внешней силы к частоте какого-либо собственного колебания данной системы. В нашем случае имеем акустический резонанс, при котором колебания частиц воздуха на выходе трубы достигают максимальной амплитуды. Это произойдет в том случае, если частота звуковых колебаний мембраны (вынуждающей силы) приближается к одной из собственных частот колебаний столба воздуха в трубе между поршнем и открытым концом. Для этого необходимо, чтобы длина Ln этого воздушного столба удовлетворяла условию:
где l - длина волны звука в трубе, n – любое целое число (n =1, 2, 3,…).
Скорость же звука
Подбор условий для получения резонанса можно осуществить двояко: при постоянной частоте n звука, а, следовательно, и длине звуковой волны l, можно изменять длину воздушного столба, получая ряд последовательных резонансов. При постепенном увеличении длины столба воздуха значения её при резонансе равны:
Отсюда следует, что волна изменить длину резонирующего столба воздуха на l/2, то полученный столб также будет резонировать. Действительно, наименьшая разность длин двух воздушных столбов, в которых возникает резонанс, равна:
Определив l, можно найти и l: Зная частоту n, находим и скорость звука:
при постоянной длине столба воздуха L1 изменяют частоту звуковых колебаний от 200 Гц и выше, определяя частоту, при которой впервые в трубе возникает резонанс. Очевидно, что в этом случае n = 1 и
Порядок выполнения Упражнение 1. Определение g при постоянной частоте звуковых колебаний (n=const) 1) Включить в сеть электронный осциллограф ЭО и звуковой генератор ЗГ. Поршень с телефоном поставить у открытого конца трубы. 2) Спустя 2-3 минуты установить на ЗГ частоту колебаний в пределах от 1000 Гц до 2000 Гц (по указанию преподавателя). 3) Подобрать напряжение на выходе генератора, чтобы на экране осциллографа наблюдались колебания достаточной амплитуды. 4) Плавно отодвигая поршень от открытого конца, последовательно пройти через все доступные для наблюдения точки резонанса, отмечая по линейке стержня соответствующие положения Ln поршня с телефоном. Данные занести в таблицу 1.
Таблица 1 Результаты измерений и вычислений
5) Вычислить расстояния между двумя последовательными положениями поршня, при которых возникает резонанс:
6) Найти среднее значение 7) Измерить температуру окружающего воздуха и найти значение g для воздуха по формуле (15), зная что 8) Найти относительную погрешность измерения g:
При следующих значениях абсолютных погрешностей
Δl=0.5·10-3м; Δν=25Гц; ΔТ=1К 9) Найти максимальную погрешность по следующей формуле
Упражнение 2. Определение g при постоянной длине воздушного столба (L = const). 1)Установить поршень с телефоном на расстояние L =15..20 см от открытого конца трубы. 2) Увеличивая частоту ЗГ от 200 Гц и выше, определить частоту, при которой в трубе впервые возникает резонанс. Для уменьшения влияния случайных ошибок на результат измерения частоты, опыт повторить несколько раз. Найти среднее значение частоты
Таблица 2 Результаты измерений и вычислений
3) Зная L, по формуле (17) найти значение скорости звука. 4) Найти значение g для воздуха по формуле (15). 5) Оценить погрешности измерения по аналогии с первым упражнением. 6) Сравнить полученные в двух упражнениях значения g с его теоретическим значением, вычисленным по формуле (8), если известно, что воздух приближенно можно рассматривать как идеальный двухатомный газ.
Контрольные вопросы 1. Уравнение Клапейрона-Менделеева. 2. Первое начало термодинамики. 3. Выражение для внутренней энергии идеального газа через число степеней свободы. 4. Виды теплоемкостей. 5. Значения молярных теплоемкостей при изопроцессах (V=const, p=const, T=const) и при адиабатическом процессе. 6. Уравнение Пуассона для адиабатического процесса. 7. Природа звука в газе. 8. Расчетная формула для нахождения g по скорости звука в газе. 9. Способы измерения скорости звука по резонансу в воздушном столбе.
Лабораторная работа №3
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-10; просмотров: 1194; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.15.135.63 (0.051 с.) |
 по скорости звука в газе
по скорости звука в газе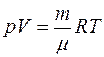 ,
,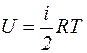 , (1)
, (1)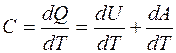
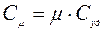
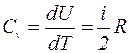 . (2)
. (2)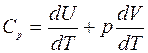 . (3)
. (3)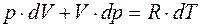 . (4)
. (4)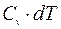 , получим окончательно:
, получим окончательно: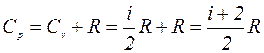 . (5)
. (5)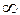 .
.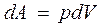
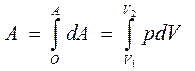
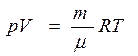
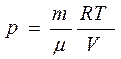
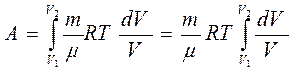
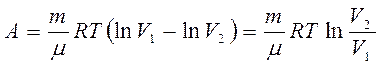
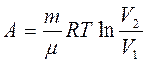
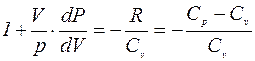 или
или 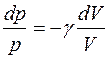 , (7)
, (7)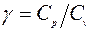 - отношение теплоемкостей, называемое показателем адиабаты.
- отношение теплоемкостей, называемое показателем адиабаты.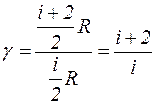 . (8)
. (8)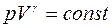 . (9)
. (9)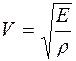 , (10)
, (10)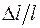 и приложенным к нему напряжением
и приложенным к нему напряжением 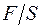 (т.е. растягивающей силе на единицу площади):
(т.е. растягивающей силе на единицу площади): , откуда
, откуда 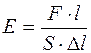 .
.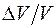 , а роль напряжения играет изменение давленая, Dр. Полагая изменения объёма и давления бесконечно малыми и принимая во внимание, что увеличение давления соответствует уменьшению объёма, для модуля упругости газа можно написать равенство:
, а роль напряжения играет изменение давленая, Dр. Полагая изменения объёма и давления бесконечно малыми и принимая во внимание, что увеличение давления соответствует уменьшению объёма, для модуля упругости газа можно написать равенство: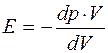 . (11)
. (11) , откуда
, откуда  . (12)
. (12)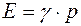 (13)
(13) (14)
(14) , откуда:
, откуда: 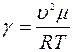 (15)
(15)
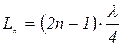 ,
,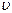 связана с его частотой n и длиной волны l соотношением:
связана с его частотой n и длиной волны l соотношением:






 . (16)
. (16) откуда l = 4L1. Зная L1=const и найдя соответствующую частоту n, находят
откуда l = 4L1. Зная L1=const и найдя соответствующую частоту n, находят  :
: (17)
(17) ,м/с
,м/с

 ;
;  ;
;  .
. вычислить скорость звука
вычислить скорость звука  ;
; 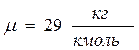



 . Данные занести в таблицу 2.
. Данные занести в таблицу 2. м/с
м/с



