
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Приближенное интегрирование функцийСтр 1 из 6Следующая ⇒
ВВЕДЕНИЕ Ни одна серьезная разработка в любой отрасли науки и производства, в том числе и в радиотехнике, не обходится без трудоемких математических расчетов. Многие серьезные радиотехнические задачи базируются на таких методах численного анализа, как вычисление определенных интегралов, решение обыкновенных дифференциальных уравнений и систем дифференциальных уравнений, регрессионный анализ и решение систем линейных уравнений. Вначале вычисления данными методами производились вручную, затем – на программируемых микрокалькуляторах. Написание программ на универсальных языках программирования, таких, как Бейсик или Паскаль, позволило значительно облегчить труд инженера. Следующим этапом автоматизации инженерных расчетов стало появление специальных математических компьютерных систем, таких, как Mathcad, Eureka, Mercury, MatLAB, Matematika, Maple и др. Системы Mathcad традиционно занимают особое место среди этих математических пакетов и по праву могут называться самыми современными, универсальными и массовыми математическими системами. Системы класса Mathcad представляют уже привычные, мощные, удобные и наглядные средства описания алгоритмов решения математических задач. ОСОБЕННОСТИ СИСТЕМЫ MATHCAD Mathcad является универсальным математическим пакетом и предоставляет пользователю одновременно оперативные возможности электронной таблицы и интерфейс WYSIWYG (What you see is what you get - что Вы видите, то и получаете). Кроме того, числовые алгоритмы, используемые Mathcad, являются общепринятыми и отличаются устойчивостью и хорошей изученностью. Mathcad позволяет выполнять как численные, так и аналитические (символьные) вычисления, имеет чрезвычайно удобный математико-ориентированный интерфейс и прекрасные средства графики. Системы начиная с версии 3.9 работают под управлением графических операционных систем Windows. Двойной щелчок на пиктограмме Mathcad вызывает появление заставки. Затем открывается окно приложения, содержащее полосу меню, палитру символов, панель инструментов и поле рабочего документа Mathcad. Для вызова меню достаточно щелкнуть по нему мышью или нажать клавишу [Alt] вместе с подчеркнутым символом. Каждая кнопка в полосе, находящейся ниже меню, открывает палитру символов, которые служат для вставки общих арифметических операторов, знаков равенства и отношения, двух- и трехмерных графиков, матричных и векторных операций, символов производных, интегралов, пределов, рядов и произведений, программных структур и греческих букв. Ниже полосы кнопок расположена панель инструментов, дублирующая наиболее часто употребляемые команды меню, и панель шрифтов, содержащая шаблоны выбора и кнопки, используемые для задания характеристик шрифтов в уравнениях и тексте. Формулы могут размещаться в любом месте рабочего документа. При этом простые выражения достаточно просто напечатать в Mathcad, а ввод более сложных уравнений облегчается специальным инструментарием. Mathcad требует от пользователя корректного описания алгоритма решения математической задачи на входном языке, очень напоминающем общепринятый язык описания математических и научно-технических расчетов.
При помощи переменных и функций в Mathcad становятся возможными связь уравнений и использование промежуточных результатов в дальнейших вычислениях. Чтобы определить любую переменную, необходимо. 1) Напечатать имя переменной, которую нужно определить. 2) Напечатать двоеточие, чтобы ввести символ определения (присваивания). 3) Напечатать значение, присваиваемое переменной. Значение может быть одиночным числом или более сложным сочетанием чисел и ранее определенных переменных. Система Mathcad содержит расширенный набор встроенных элементарных функций (более 250). Функции задаются своим именем и значением аргумента в круглых скобках. В ответ на обращения к ним функции возвращают вычисленные значения. Аргумент и значение функций могут быть действительными или комплексными числами. Для вызова встроенных функций достаточно нажать кнопку ¦
Несмотря на довольно широкий набор встроенных функций, всегда возникает необходимость расширить систему новыми функциями, представляющими интерес для пользователя. Функции пользователя вводятся с применением следующего выражения: Имя_функции (Список_параметров): = Выражение Имя функции задается как любой идентификатор. В скобках указывается список параметров функции, т.е. перечень используемых в выражении переменных, разделяемых запятыми. Выражение - любое выражение, содержащее доступные системе операторы и функции с операндами и аргументами, указанными в списке параметров. В качестве примера использования функции при вычислениях рассмотрим решение одного уравнения с одним неизвестным с помощью функции root. Аргументами этой функции является выражение и переменная, входящая в выражение: root(f(z),z). Функция возвращает значение переменной z, при котором заданное выражение обратится в ноль. Оба аргумента функции root должны быть скалярами, с векторами и матрицами она работать не может. Второму аргументу – имени переменной – до вызова функции root необходимо присвоить какое-либо значение, которое Mathcad будет использовать как начальное приближение при поиске корня. Эта возможность особенно полезна, если имеется несколько решений. Тогда выбор решения определяется выбором начального значения переменной. Первым аргументом должна быть либо определенная ранее собственная функция пользователя, либо собственно выражение. В любом случае выражение – это левая часть уравнения Таким образом, если дано уравнение
Набрав после этого Также функцию root можно использовать не с 2-я, а с 4-я аргументами, где кроме выражения и переменной указываются границы интервала нахождения корня. Например Mathcad может строить двумерные графики в декартовых и полярных координатах, картины линий уровня, изображать поверхности и выводить ряд других трехмерных графиков. Чтобы создать график в Mathcad, нужно щелкнуть мышью на том свободном месте, где его нужно разместить, и выбрать нужный пункт из меню Графика. Появляется пустой график с полями ввода для выражений, отображаемых по осям графика. Множества точек, из которых состоит график, определяются дискретными аргументами: Mathcad строит одну точку графика для каждого значения дискретного аргумента, задающего график. Поле ввода возникнет под осью абсцисс. В него нужно ввести имя переменной, установив, таким образом, соответствие этой оси с переменной. Теперь нужно щелкнуть в поле напротив середины оси ординат и ввести здесь функцию, указав Mathcad откладывать значения этой функции по данной оси. Остающиеся поля предназначены для ввода границ на осях максимального и минимального значений, откладываемых на оси. Если оставить их пустыми, Mathcad автоматически заполнит их при создании графика. После щелчка вне графика Mathcad вычисляет и строит точки графика. Под ординатой появляется образец линии, которой нарисован график. Это помогает идентифицировать различные кривые, если на одно поле выводятся несколько графиков. По умолчанию Mathcad соединяет точки прямыми линиями и устанавливает пределы по осям.
Mathcad имеет интерактивную справочную систему, вызываемую нажатием клавиши [F1]. Совокупность часто используемых процедур Mathcad оформлена в виде набора легкодоступных документов - шпаргалок QuickSheets. Формулы или изображения из Электронных Книг Mathcad могут быть перенесены в рабочий документ простым щелчком мыши. Сохранение и печать рабочего документа Mathcad осуществляется стандартно для Windows-программ. Метод выбранных точек Пусть для системы опытных данных
содержащая m (m<n) свободных параметров На координатной плоскости Oxy с возможной аккуратностью проводим плавную кривую Г, наиболее близко примыкающую к точкам
Для случая квадратичной зависимости
Заметим, что метод выбранных точек содержит геометрические построения, допускающие известный произвол, и поэтому является грубым. К нему следует прибегать в тех случаях, когда точность исходных данных относительно невелика. Для увеличения точности метода рекомендуется пользоваться сеткой с мелкими делениями. Достоинство метода – простота применения и наглядность. Метод средних Если в эмпирическую формулу
подставить исходные данные
называются уклонениями и представляют собой расстояния по вертикали точек Согласно методу средних за наилучшее положение эмпирической кривой К принимается то, для которого равна нулю алгебраическая сумма Е всех уклонений
Для определения по методу средних постоянных Решив эту систему, найдём коэффициенты Метод наименьших квадратов Пусть известен вид эмпирической формулы
и Согласно методу наименьших квадратов наилучшими коэффициентами
будет минимальной. Отсюда, используя необходимые условия экстремума функции нескольких переменных, получаем так называемую нормальную систему для определения коэффициентов
Если система (10) единственное решение, то оно будет искомым. Система (10) упрощается, если эмпирическая функция
где
Отсюда
Введя сокращенные обозначения
В частном случае, если эмпирическая функция представляет полином
Следовательно, нормальная система (11’) будет иметь вид
Метод наименьших квадратов обладает тем преимуществом, что если сумма S квадратов уклонений Недостатком метода наименьших квадратов является громоздкость вычислений. Поэтому к нему прибегают обычно при обработке наблюдений высокой точности, когда нужно получить также весьма точные значения параметров. Заметим, что в этом случае промежуточные вычисления нужно проводить с надлежащим количеством десятичных знаков, так как в противном случае при неблагоприятных условиях искомые коэффициенты будут иметь мало верных знаков. Но грубые значения этих коэффициентов могут быть получены значительно проще, т.е. применение метода не будет оправданно. В частности, если происходит потеря цифр при вычитании, то вычисления должны быть проведены с достаточным количеством запасных верных значащих цифр. Здесь следует руководствоваться следующим правилом: если численные значения коэффициентов желательно иметь с m верными значащими цифрами и если предварительные вычисления показывают, что первые p цифр исчезнут при вычитании, то вычисления должны быть произведены с m + p + 1 верными значащими цифрами на всех стадиях работы. Линейная регрессия Для проведения линейной регрессии в систему встроен ряд приведенных ниже функций: corr( VX, VY ) – возвращает скаляр – коэффициент корреляции Пирсона; intercrpt( VX, VY ) – возвращает значение параметра а (смещение линии регрессии по вертикали);
slope( VX, VY ) – возвращает значение параметра b (наклона линии регрессии). Эти функции возвращают угловые коэффициенты линии с наименьшей площадью отклонений. Если Вы размещаете ваши значения x в вектор Vx, а значения y в Vy, получается линия: Обозначения: Vx - вектор реальных значений данных в восходящем порядке для функции отрезка, отсекаемого на координатной оси. (Значения в Vx соответствуют значениям x; Vy - вектор реальных значений данных). Они соответствуют значениям y, число элементов то же самое, что и у Vx. Параболическая регрессия Введена в MathCAD и функция для обеспечения полиномиальной (параболической)регрессии при произвольной степени полинома регрессии regress( VX,VY,n ). Она возвращает вектор VS, запрашиваемый функцией interp (VS,VX,VY,x), содержащий коэффициенты многочлена п-й степени, который наилучшим образом приближает “облако” точек с координатами, хранящимися в векторах VX и VY. На практике не рекомендуется делать степень аппроксимирующего полинома выше четвертой - шестой, поскольку погрешности реализации регрессии сильно возрастают. Функция regress создает единственный приближающий полином, коэффициенты которого вычисляются по всей совокупности заданных точек, т.е. глобально. Иногда полезна другая функция полиномиальной регрессии, дающая локальные приближения отрезками полиномов второй степени, Линейная комбинация функций При выполнении в Mathcad линейной регрессии общего вида заданная совокупность точек приближается функцией вида F(x, К1,К2,., Kn)= K1, F1(x)+K2 F2(x)+ +КnFn(x) Таким образом, функция регрессии является линейной комбинацией функций F1(x), F2(x),., Fn(x), причем сами эти функции могут быть нелинейными, что резко расширяет возможности такой аппроксимации и распространяет ее на нелинейные функции. Для реализации линейной регрессии общего вида используется функция linfit( VX,VY,F ). Эта функция возвращает вектор коэффициентов линейной регрессии общего вида К, при котором среднеквадратичная погрешность приближения облака исходных точек, если их координаты хранятся в векторах VX и VY, оказывается минимальной. Вектор F должен содержать функции F1(x), F2(x),, Fn(x), записанные в символьном виде. Расположение координат точек исходного массива может быть любым, но вектор VX должен содержать координаты, упорядоченные в порядке их возрастания, а вектор VY ординаты, соответствующие абсциссам в векторе VX. Оператор Add Line Оператор Add Line выполняет функции расширения программного блока. Расширение фиксируется удлинением вертикальной черты программных блоков или их древовидным расширением. Благодаря этому в принципе можно создавать сколь угодно большие программы. Оператор ← Оператор ← выполняет функции внутреннего локального присваивания. Например, выражение х ← 123 присваивает переменной х значение 123. Локальный характер присваивания означает, что такое значение х сохраняет только в теле программы. За пределами тела программы значение переменной х может быть неопределенным либо равным значению, которое задается операторами локального: = и глобального = присваивания вне программного блока. Оператор if Оператор if является оператором условного выражения. Он задается в виде: Выражение if Условие Если Условие выполняется, то возвращается значение Выражения. Совместно с этим оператором часто используются оператор прерывания break и оператор иного выбора otherwise. Оператор for Оператор for служит для организации циклов с заданным числом повторений. Он записывается в виде: for Var e Nmin.. Nmax
Эта запись означает, что если переменная Var меняется с шагом +1 от значения Nmin до значения Nmax, то выражение, помещенное в шаблон, будет выполняться. Переменную счетчика Var можно использовать в выражениях программы. Оператор while Оператор while служит для организации циклов, действующих до тех пор, пока выполняется некоторое Условие. Этот оператор записывается в виде: While Условие
Выполняемое выражение записывается на место шаблона. Оператор otherwise Оператор иного выбора otherwise обычно используется совместно с оператором if. Это поясняет следующая программная конструкция: f (x): = 1 if х>0 возвращает 1, если х > 0 -1 otherwise возвращает -1 во всех иных случаях Оператор break Оператор break вызывает прерывание работы программы всякий раз, когда он встречается. Чаще всего он используется совместно с оператором условного выражения if и операторами циклов while и for, обеспечивая переход в конец тела цикла. Оператор continue Оператор continue используется для продолжения работы после прерывания программы. Обычно он применяется совместно с операторами задания циклов while и for, обеспечивая после прерывания возврат в начало цикла. Оператор return Оператор return прерывает выполнение программы и возвращает значение своего операнда, стоящего следом за ним. Например, в приведенном ниже случае return 0 if x<0 будет возвращаться значение 0 при любом х < 0. Оператор on error Оператор on error является оператором обработки ошибок, позволяющим создавать конструкции обработчиков ошибок. Этот оператор задается в виде: Выражение_1 on error Выражение_2 Если при выполнении Выражения_1 возникает ошибка, то выполняется Выражение_2. С оператором on error связана функция error, которая обычно используется для возврата текстового сообщения об ошибке. ЗАКЛЮЧЕНИЕ Овладение рассмотренными численными методами, способами их алгоритмизации для реализации на языках программирования высокого уровня, освоение возможностей пакета Mathcad позволит современному радиоинженеру легко справляться с большинством возникающих на практике вычислительных задач. БИБЛИОГРАФИЧЕСКИЙ СПИСОК 1. Демидович Б. П., Марон И. А., Шувалова Э. З. Численные методы анализа. - М.: Физматгиз, 1963. 2. Копченова Н. В., Марон И. А. Вычислительная математика в примерах и задачах. - М.: Наука, 1972. 3. Mathcad 6.0 PLUS. Финансовые, инженерные и научные расчеты в среде Windows 95./Перевод с англ. - М.: Информационно-издательский дом “Филинъ”, 1996. ПРИЛОЖЕНИЕ Содержание
ВВЕДЕНИЕ.. 2 1. ОСОБЕННОСТИ СИСТЕМЫ MATHCAD.. 2 2. ПРИБЛИЖЕННОЕ ИНТЕГРИРОВАНИЕ ФУНКЦИЙ.. 2 3. ПРИБЛИЖЕННЫЕ МЕТОДЫ РЕШЕНИЯ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ.. 2 4. ОПРЕДЕЛЕНИЕ ПАРАМЕТРОВ ЭМПИРИЧЕСКОЙ ФОРМУЛЫ (РЕГРЕССИОННЫЙ АНАЛИЗ) 2 5.РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ.. 2 6. ВОЗМОЖНОСТИ ПРОГРАММИРОВАНИЯ В MATHCAD.. 2 ЗАКЛЮЧЕНИЕ.. 2 БИБЛИОГРАФИЧЕСКИЙ СПИСОК. 2 ПРИЛОЖЕНИЕ.. 2
ВВЕДЕНИЕ Ни одна серьезная разработка в любой отрасли науки и производства, в том числе и в радиотехнике, не обходится без трудоемких математических расчетов. Многие серьезные радиотехнические задачи базируются на таких методах численного анализа, как вычисление определенных интегралов, решение обыкновенных дифференциальных уравнений и систем дифференциальных уравнений, регрессионный анализ и решение систем линейных уравнений. Вначале вычисления данными методами производились вручную, затем – на программируемых микрокалькуляторах. Написание программ на универсальных языках программирования, таких, как Бейсик или Паскаль, позволило значительно облегчить труд инженера. Следующим этапом автоматизации инженерных расчетов стало появление специальных математических компьютерных систем, таких, как Mathcad, Eureka, Mercury, MatLAB, Matematika, Maple и др. Системы Mathcad традиционно занимают особое место среди этих математических пакетов и по праву могут называться самыми современными, универсальными и массовыми математическими системами. Системы класса Mathcad представляют уже привычные, мощные, удобные и наглядные средства описания алгоритмов решения математических задач. ОСОБЕННОСТИ СИСТЕМЫ MATHCAD Mathcad является универсальным математическим пакетом и предоставляет пользователю одновременно оперативные возможности электронной таблицы и интерфейс WYSIWYG (What you see is what you get - что Вы видите, то и получаете). Кроме того, числовые алгоритмы, используемые Mathcad, являются общепринятыми и отличаются устойчивостью и хорошей изученностью. Mathcad позволяет выполнять как численные, так и аналитические (символьные) вычисления, имеет чрезвычайно удобный математико-ориентированный интерфейс и прекрасные средства графики. Системы начиная с версии 3.9 работают под управлением графических операционных систем Windows. Двойной щелчок на пиктограмме Mathcad вызывает появление заставки. Затем открывается окно приложения, содержащее полосу меню, палитру символов, панель инструментов и поле рабочего документа Mathcad. Для вызова меню достаточно щелкнуть по нему мышью или нажать клавишу [Alt] вместе с подчеркнутым символом. Каждая кнопка в полосе, находящейся ниже меню, открывает палитру символов, которые служат для вставки общих арифметических операторов, знаков равенства и отношения, двух- и трехмерных графиков, матричных и векторных операций, символов производных, интегралов, пределов, рядов и произведений, программных структур и греческих букв. Ниже полосы кнопок расположена панель инструментов, дублирующая наиболее часто употребляемые команды меню, и панель шрифтов, содержащая шаблоны выбора и кнопки, используемые для задания характеристик шрифтов в уравнениях и тексте. Формулы могут размещаться в любом месте рабочего документа. При этом простые выражения достаточно просто напечатать в Mathcad, а ввод более сложных уравнений облегчается специальным инструментарием. Mathcad требует от пользователя корректного описания алгоритма решения математической задачи на входном языке, очень напоминающем общепринятый язык описания математических и научно-технических расчетов. При помощи переменных и функций в Mathcad становятся возможными связь уравнений и использование промежуточных результатов в дальнейших вычислениях. Чтобы определить любую переменную, необходимо. 1) Напечатать имя переменной, которую нужно определить. 2) Напечатать двоеточие, чтобы ввести символ определения (присваивания). 3) Напечатать значение, присваиваемое переменной. Значение может быть одиночным числом или более сложным сочетанием чисел и ранее определенных переменных. Система Mathcad содержит расширенный набор встроенных элементарных функций (более 250). Функции задаются своим именем и значением аргумента в круглых скобках. В ответ на обращения к ним функции возвращают вычисленные значения. Аргумент и значение функций могут быть действительными или комплексными числами. Для вызова встроенных функций достаточно нажать кнопку ¦ Несмотря на довольно широкий набор встроенных функций, всегда возникает необходимость расширить систему новыми функциями, представляющими интерес для пользователя. Функции пользователя вводятся с применением следующего выражения: Имя_функции (Список_параметров): = Выражение Имя функции задается как любой идентификатор. В скобках указывается список параметров функции, т.е. перечень используемых в выражении переменных, разделяемых запятыми. Выражение - любое выражение, содержащее доступные системе операторы и функции с операндами и аргументами, указанными в списке параметров. В качестве примера использования функции при вычислениях рассмотрим решение одного уравнения с одним неизвестным с помощью функции root. Аргументами этой функции является выражение и переменная, входящая в выражение: root(f(z),z). Функция возвращает значение переменной z, при котором заданное выражение обратится в ноль. Оба аргумента функции root должны быть скалярами, с векторами и матрицами она работать не может. Второму аргументу – имени переменной – до вызова функции root необходимо присвоить какое-либо значение, которое Mathcad будет использовать как начальное приближение при поиске корня. Эта возможность особенно полезна, если имеется несколько решений. Тогда выбор решения определяется выбором начального значения переменной. Первым аргументом должна быть либо определенная ранее собственная функция пользователя, либо собственно выражение. В любом случае выражение – это левая часть уравнения Таким образом, если дано уравнение
Набрав после этого Также функцию root можно использовать не с 2-я, а с 4-я аргументами, где кроме выражения и переменной указываются границы интервала нахождения корня. Например Mathcad может строить двумерные графики в декартовых и полярных координатах, картины линий уровня, изображать поверхности и выводить ряд других трехмерных графиков. Чтобы создать график в Mathcad, нужно щелкнуть мышью на том свободном месте, где его нужно разместить, и выбрать нужный пункт из меню Графика. Появляется пустой график с полями ввода для выражений, отображаемых по осям графика. Множества точек, из которых состоит график, определяются дискретными аргументами: Mathcad строит одну точку графика для каждого значения дискретного аргумента, задающего график. Поле ввода возникнет под осью абсцисс. В него нужно ввести имя переменной, установив, таким образом, соответствие этой оси с переменной. Теперь нужно щелкнуть в поле напротив середины оси ординат и ввести здесь функцию, указав Mathcad откладывать значения этой функции по данной оси. Остающиеся поля предназначены для ввода границ на осях максимального и минимального значений, откладываемых на оси. Если оставить их пустыми, Mathcad автоматически заполнит их при создании графика. После щелчка вне графика Mathcad вычисляет и строит точки графика. Под ординатой появляется образец линии, которой нарисован график. Это помогает идентифицировать различные кривые, если на одно поле выводятся несколько графиков. По умолчанию Mathcad соединяет точки прямыми линиями и устанавливает пределы по осям. Mathcad имеет интерактивную справочную систему, вызываемую нажатием клавиши [F1]. Совокупность часто используемых процедур Mathcad оформлена в виде набора легкодоступных документов - шпаргалок QuickSheets. Формулы или изображения из Электронных Книг Mathcad могут быть перенесены в рабочий документ простым щелчком мыши. Сохранение и печать рабочего документа Mathcad осуществляется стандартно для Windows-программ. ПРИБЛИЖЕННОЕ ИНТЕГРИРОВАНИЕ ФУНКЦИЙ Если функция Однако во многих случаях первообразная функция Заменяя подынтегральную функцию интерполяционным многочленом, получаем квадратурные формулы вида
где
Вычисляется подынтегральная функция в полученных узлах
Квадратурные формулы для равностоящих узлов называются формулами Ньютона-Котеса. Формулы Ньютона-Котеса различаются степенями использованных интерполяционных многочленов. Чтобы не иметь дело с многочленами высоких степеней, промежуток интегрирования обычно разбивают на отдельные участки, применяют формулы Ньютона-Котеса с невысокими степенями на каждом участке и потом складывают полученные результаты (что дает так называемые составные формулы). Наиболее простые из формул такого типа приведены ниже.
Формула трапеций (рис. 1):
где
Рис.1.
Остаточный член имеет вид
|
|||||||||
|
Последнее изменение этой страницы: 2016-12-10; просмотров: 425; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.15.1 (0.162 с.) |
 на панели инструментов или вызвать пункт Function из меню Insert(Вставка). Операция Choose function... (Выбрать функцию) выполняет следующие действия: выводит полный перечень встроенных в ядро системы функций; кратко поясняет назначение каждой функции; позволяет корректно ввести шаблон с именем функции в место расположения курсора, установленного в математическом выражении. На месте параметров в выведенной функции имеются шаблоны данных для их ввода.
на панели инструментов или вызвать пункт Function из меню Insert(Вставка). Операция Choose function... (Выбрать функцию) выполняет следующие действия: выводит полный перечень встроенных в ядро системы функций; кратко поясняет назначение каждой функции; позволяет корректно ввести шаблон с именем функции в место расположения курсора, установленного в математическом выражении. На месте параметров в выведенной функции имеются шаблоны данных для их ввода. .
. , то для решения в Mathcad предварительно его надо переписать в виде
, то для решения в Mathcad предварительно его надо переписать в виде  . Теперь в Mathcad набираем:
. Теперь в Mathcad набираем:
 или
или 


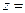 , получаем на экране значение корня данного уравнения.
, получаем на экране значение корня данного уравнения.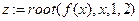 .
. построена эмпирическая формула
построена эмпирическая формула (6)
(6) , где
, где  известная функция.
известная функция. . На кривой Г выбираем систему m (по числу параметров) точек
. На кривой Г выбираем систему m (по числу параметров) точек  , не обязательно совпадающих с точками
, не обязательно совпадающих с точками  были по возможности равномерно распределены по всей рабочей части кривой Г и возможно дальше отстояли друг от друга, и в то же время не лежали бы слишком близко к мало надёжным концевым точкам
были по возможности равномерно распределены по всей рабочей части кривой Г и возможно дальше отстояли друг от друга, и в то же время не лежали бы слишком близко к мало надёжным концевым точкам  и
и  . Для удобства обычно берут абсциссы
. Для удобства обычно берут абсциссы  этих точек совпадающими с крупными делениями оси Ox координатной сетки. После этого со всей тщательностью замеряют координаты
этих точек совпадающими с крупными делениями оси Ox координатной сетки. После этого со всей тщательностью замеряют координаты  . Тогда параметры
. Тогда параметры  , в общем случае, могут быть определены из системы m уравнений
, в общем случае, могут быть определены из системы m уравнений


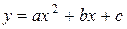 коэффициенты a, b и c определяются из системы трёх уравнений
коэффициенты a, b и c определяются из системы трёх уравнений
 (7)
(7) , то левая часть формулы, вообще говоря, не будет равна правой. Разности (невязки)
, то левая часть формулы, вообще говоря, не будет равна правой. Разности (невязки)

 от графика эмпирической функции (7), взятые со знаком плюс (+) или со знаком минус (-).
от графика эмпирической функции (7), взятые со знаком плюс (+) или со знаком минус (-). , т.е. должно иметь место равенство
, т.е. должно иметь место равенство (8)
(8) , где m < n, все уклонения
, где m < n, все уклонения  уклонений, входящих в каждую из этих групп, получаем систему, содержащую столько уравнений, сколько имеется неизвестных коэффициентов
уклонений, входящих в каждую из этих групп, получаем систему, содержащую столько уравнений, сколько имеется неизвестных коэффициентов  . Заметим, что поскольку сумма
. Заметим, что поскольку сумма  уклонений для каждой группы равна нулю, то равна нулю также и сумма Е всех уклонений, т.е. для нашей системы равенство (8) будет выполнено.
уклонений для каждой группы равна нулю, то равна нулю также и сумма Е всех уклонений, т.е. для нашей системы равенство (8) будет выполнено. (9)
(9)
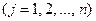 - уклонения эмпирической формулы (9) от исходных данных (
- уклонения эмпирической формулы (9) от исходных данных (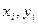 ).
). считаются те, для которых сумма квадратов уклонений
считаются те, для которых сумма квадратов уклонений

 (10)
(10) линейная относительно параметров
линейная относительно параметров  ,
,
 (11)
(11) и
и  , систему (5) можно записать в виде нормальной системы
, систему (5) можно записать в виде нормальной системы (11’)
(11’) то:
то: и
и 

 мала, то сами эти уклонения также малы по абсолютной величине. Для метода средних, где составляется алгебраическая сумма уклонений, такого вывода сделать нельзя.
мала, то сами эти уклонения также малы по абсолютной величине. Для метода средних, где составляется алгебраическая сумма уклонений, такого вывода сделать нельзя. непрерывна на [a, b] и известна ее первообразная
непрерывна на [a, b] и известна ее первообразная  , то определенный интеграл от этой функции в пределах от а до b может быть вычислен по формуле Ньютона-Лейбница:
, то определенный интеграл от этой функции в пределах от а до b может быть вычислен по формуле Ньютона-Лейбница:  где
где  .
. часто задается таблично, и тогда понятие первообразной теряет смысл. Аналогичные вопросы возникают и при вычислении кратных интегралов. Поэтому большое значение имеют приближенные и в первую очередь численные методы интегрирования.
часто задается таблично, и тогда понятие первообразной теряет смысл. Аналогичные вопросы возникают и при вычислении кратных интегралов. Поэтому большое значение имеют приближенные и в первую очередь численные методы интегрирования.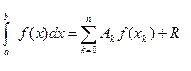
 - выбранные узлы интерполяции,
- выбранные узлы интерполяции,  - коэффициенты, зависящие только от выбора узлов, но не от вида функции
- коэффициенты, зависящие только от выбора узлов, но не от вида функции 
 - остаточный член, или погрешность квадратурной формулы. При отбрасывании остаточного члена R появляется погрешность усечения. В расчете отрезок интегрирования
- остаточный член, или погрешность квадратурной формулы. При отбрасывании остаточного члена R появляется погрешность усечения. В расчете отрезок интегрирования  разбивается на n равных частей системой точек
разбивается на n равных частей системой точек (i=0, 1, …, n),
(i=0, 1, …, n),  ,
,  ,
, 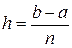 .
. (i=0, 1, …, n).
(i=0, 1, …, n).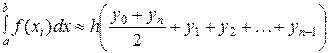 ,
, (i=0, 1, …, n).
(i=0, 1, …, n).



