
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Выбор вида математической модели⇐ ПредыдущаяСтр 13 из 13
Как мы выяснили, через n точек можно всегда провести кривую, аналитически выражаемую многочленом (n - 1) -й степени. Этот многочлен называют интерполяционным. И вообще, замену функции
Рис. 33.13. Сглаживание функцией supsmooth.
Однако такое решение проблемы не является удовлетворительным, поскольку
где Как правило, регрессия очень эффективна, когда заранее известен (или, по крайней мере, хорошо угадывается) закон распределения данных. Задача выбора вида функциональной зависимости - задача не формализуемая, так как одна и та же кривая на данном участке примерно с одинаковой точностью может быть описана самыми различными аналитическими выражениями. Так, например, U - образная кривая может быть описана участком параболы, гиперболы, эллипса или синусоиды. Рациональный выбор того или иного аналитического описания может быть обоснован лишь при учете определенного перечня требований. Главное требование к математической модели - это удобство ее последующего использования. Основное, что обеспечивает удобство математического выражения, - его компактность. Например, известно, что любую функцию Другое весьма желательное (но не всегда достижимое) требование – это содержательность, иначе говоря, интерпретируемость предлагаемого аналитического описания. Как правило, это достигается путем придания определенного смысла константам или функциям, входящим в найденную математическую модель. Отсюда следует важное практическое обстоятельство. Даже в наше время широкого использования компьютеров в научных исследованиях принятие решения о выборе той или иной математической модели остается за человеком - исследователем и не может быть передано компьютеру. Только человек, а не компьютер, знает, для чего будет в дальнейшем использоваться эта модель, на основе каких понятий будут интерпретированы ее параметры и т. д.
Если подбор вида аппроксимирующей функции - процесс не формальный и не может быть полностью передан компьютеру, то расчет параметров аппроксимирующей функции выбранного вида - операция чисто формальная и ее следует осуществлять на компьютере. Более того, это трудный и утомительный процесс, в котором человек не застрахован от ошибок, а компьютер выполнит его быстрее и качественнее. В общем случае этот расчет состоит в решении системы нелинейных уравнений. В частных случаях это может быть система уравнений линейных относительно искомых параметров, система уравнений, которые после ряда преобразований сводятся к линейным и, наконец, когда уравнения системы не сводятся к линейным. Так, например, если известны координаты Как видно из этого примера, число независимых уравнений системы равно числу n поставленных опытов. С другой стороны, для определения k коэффициентов необходимо не менее k независимых уравнений. Но если число n поставленных опытов и число независимых уравнений равно числу искомых коэффициентов, то решение системы единственно, а следовательно, случайно, так как точно соответствует случайным значениям исходных данных. При числе опытов n, большем, чем число k искомых коэффициентов, число независимых уравнений системы избыточно. Из этих уравнений в разных комбинациях можно составить несколько систем уравнений, каждая из которых в отдельности даст свое решение. Но между собой они будут несовместимы. Каждое решение будет соответствовать своей аппроксимирующей функции. Если все их построить на графике, то получим целый пучок аппроксимирующих кривых.
Это открывает при n > k совершенно новые возможности. Во-первых, этот пучок кривых показывает форму и ширину области неопределенности проведенного эксперимента. Во-вторых, может быть произведено усреднение всех найденных кривых. Полученная усредненная кривая будет гораздо точнее и достовернее описывать исследованное явление, так как она в значительной степени освобождена от случайных погрешностей, приводящих к разбросу отдельных экспериментальных точек. Таким образом, проведение большего числа опытов n, чем минимально необходимое для расчета коэффициентов n = k, позволяет определить область неопределенности по фактическим данным эксперимента и одновременно существенно уменьшить случайную погрешность окончательного результата путем усреднения.
Метод наименьших квадратов.
Усреднение несовместных решений избыточной системы уравнений может быть произведено различными способами (на глаз, методом медианных центров и т. д.). Наиболее мощный метод был разработан в 1795-180 гг. Лежандром и Гауссом и получил название регрессионного анализа, или метода наименьших квадратов (МНК). Но теперь благодаря возможности широкого доступа исследователей к вычислительной технике этот метод получил второе рождение. Дело в том, что вычисления по МНК черезвычайно громоздки. С появлением компьютеров положение коренным образом изменилось. Программы обработки данных МНК содержатся в математическом обеспечении любого компьютера. Поэтому практически надо только ввести свои данные в соответствии с этой программой и дождаться готового ответа. Но чтобы представлять себе, что делает с нашими данными компьютер по программам МНК, рассмотрим сущность МНК на примере простейших задач. Задача аппроксимации решается следующим образом. В декартовой прямоугольной системе координат наносят точки (xi, yi). По расположению этих точек высказывается предположение о принадлежности искомой функции к определенному классу функций. Например, линейная функция
Величина
Отсюда и наименование: метод наименьших квадратов. Решая систему уравнений (33.13), находим неизвестные параметры aj и тем самым полностью определяем функцию, которая наилучшим образом (в смысле наименьших квадратов отклонений от исходных точек или наименьшей суммарной невязки) аппроксимирует (приближает) искомую функцию
Линейная зависимость.
Остановимся подробнее на линейной зависимости.
Задача состоит в том, чтобы найти параметры m и c, при которых прямая наилучшим образом проходила бы через экспериментальные точки. Линейная зависимость очень широко распространена в физике. И даже когда зависимость нелинейная, обычно стараются строить график так, чтобы получить прямую линию.
Допустим, что имеется n пар измеренных значений В случае параметров m и c отклонение в i -м измерении составляет
Наилучшие значения m и c выбираются так, чтобы сумма
была минимальной.
Таким образом, искомые величины m и c получаются решением системы уравнений
Второе уравнение показывает, что наилучшая прямая проходит через точку с координатами
т.е. через центр тяжести всех экспериментальных точек. Из уравнений находим
Результат обработки данных линейной зависимостью методом наименьших квадратов средствами Mathcad показан на рисунках 33.14 - 33.14.
Рис. 33.14: Метод наименьших квадратов. Аппроксимация линейной зависимостью средствами Mathcad. Линеаризация
Ввиду простоты расчетов, линейная зависимость используется довольно часто. Кроме того, многие функции, зависящие от двух параметров, можно линеаризовать путем замены переменных. Для этого необходимо подобрать такое преобразование исходной зависимости Для ряда часто встречающихся двухпараметрических зависимостей возможные замены переменных приведены в Таблице 33.1.
Таблица 33.1.
Полиномиальная регрессия
Еще одним из наиболее распространенных вариантов обработки набора данных однофакторного эксперимента является аппроксимация полиномами.
Рис. 20: Реализация экспоненциальной регрессии.
Рассмотрим полином
где Метод наименьших квадратов требует, чтобы сумма квадратов отклонений, т. е. квадратов остатков, была минимальной. Она определяется следующим образом
где n - число пар экспериментальных данных (xi, yi). Минимизируем R стандартным методом. Для этого определим производные по каждому из параметров и приравняем их к нулю.
В результате мы имеем систему из m уравнений, линейных по неизвестным коэффициентам полинома
где суммирование производится по всем точкам. Преобразуя систему уравнений, получим
Систему линейных уравнений удобно представить в матричном обозначении Aa = b. Матрица A - квадратная симметричная матрица, a - вектор коэффициентов полинома, b - вектор свободных членов.
Элементы матрицы A легко записать следующим образом
где j - номер строки, k - номер столбца. Подобным же образом запишем выражение для b
Из линейной алгебры вы знаете, что решение для вектора a можно найти следующим образом
Среднеквадратичная ошибка подгонки и ошибки подгоночных параметров определяются выражениями
Качество аппроксимации полиномами различных степеней можно оценить сравнивая значения ѕ. Обратите внимание, что эта величина зависит от разности числа экспериментальных точек и числа подгоночных параметров.
|
||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-13; просмотров: 412; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.178.133 (0.061 с.) |
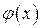 на функцию
на функцию  так, что их значения совпадают в заданных точках
так, что их значения совпадают в заданных точках 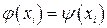 называют интерполяцией.
называют интерполяцией.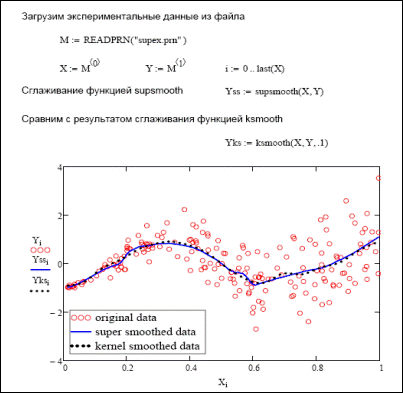
 из-за случайных ошибок измерения и влияния на измерения значений
из-за случайных ошибок измерения и влияния на измерения значений 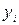 помех и шумов в устройстве. Так что
помех и шумов в устройстве. Так что , (33.11)
, (33.11) - некоторая случайная ошибка. Поэтому требуется провести кривую так, чтобы она в наименьшей степени зависела от случайных ошибок. Эта задача называется сглаживанием (аппроксимацией) экспериментальной зависимости и часто решается методом наименьших квадратов. Сглаживающую кривую называют аппроксимирующей.
- некоторая случайная ошибка. Поэтому требуется провести кривую так, чтобы она в наименьшей степени зависела от случайных ошибок. Эта задача называется сглаживанием (аппроксимацией) экспериментальной зависимости и часто решается методом наименьших квадратов. Сглаживающую кривую называют аппроксимирующей. можно описать многочленом
можно описать многочленом 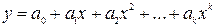 . Но если же оказывается возможным с приемлемой точностью описать ее одночленом вида
. Но если же оказывается возможным с приемлемой точностью описать ее одночленом вида  ,
,  и т. п., то ясно, что такое компактное представление много лучше. Таким образом, компактность модели достигается удачным выбором элементарных функций, обеспечивающих хорошее приближение при малом их числе.
и т. п., то ясно, что такое компактное представление много лучше. Таким образом, компактность модели достигается удачным выбором элементарных функций, обеспечивающих хорошее приближение при малом их числе.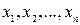 и
и  для n экспериментальных точек, а для аппроксимации принята модель в виде многочлена
для n экспериментальных точек, а для аппроксимации принята модель в виде многочлена  по известным координатам n точек сводится к решению системы уравнений, линейных относительно коэффициентов.
по известным координатам n точек сводится к решению системы уравнений, линейных относительно коэффициентов.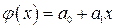 , квадратичная
, квадратичная 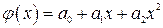 и т.д. В общем случае
и т.д. В общем случае  . Неизвестные параметры функции
. Неизвестные параметры функции  определяются из требования минимума суммы квадратов случайных ошибок, т. е. минимума величины
определяются из требования минимума суммы квадратов случайных ошибок, т. е. минимума величины (33.12)
(33.12) называется также суммарной невязкой. Необходимым условием минимума функции нескольких переменных является обращение в нуль частных производных невязки:
называется также суммарной невязкой. Необходимым условием минимума функции нескольких переменных является обращение в нуль частных производных невязки: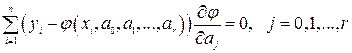 . (33.13)
. (33.13) . (33.14)
. (33.14) ,
,  , …,
, …,  и предположим, что ошибки содержат лишь величины y. Такое предположение очень часто оправдывается на практике. В противном случае анализ существенно усложняется.
и предположим, что ошибки содержат лишь величины y. Такое предположение очень часто оправдывается на практике. В противном случае анализ существенно усложняется. . (33.15)
. (33.15)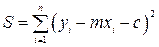 (33.16)
(33.16) . (33.17)
. (33.17) . (33.18)
. (33.18) , (33.19)
, (33.19) . (33.20)
. (33.20)

 , в результате которого зависимость приобретает линейный вид
, в результате которого зависимость приобретает линейный вид 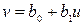 . Далее решается задача линейной аппроксимации для новой зависимости и вычисленные коэффициенты b0 и b1 пересчитываются в коэффициенты a0 и a1.
. Далее решается задача линейной аппроксимации для новой зависимости и вычисленные коэффициенты b0 и b1 пересчитываются в коэффициенты a0 и a1.

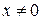
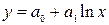





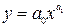
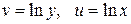
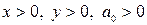
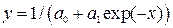



 , (33.21)
, (33.21)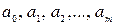 - подгоночные параметры, m - степень полинома.
- подгоночные параметры, m - степень полинома.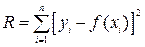 , (33.22)
, (33.22) . (33.23)
. (33.23) , (33.24)
, (33.24) (33.25)
(33.25)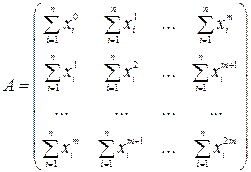 , (33.26)
, (33.26) , (33.27)
, (33.27) . (33.28)
. (33.28) , (33.29)
, (33.29) . (33.30)
. (33.30) . (33.31)
. (33.31) . (33.32)
. (33.32)


