
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Этот метод применим для любых СЛАУ, в том числе вырожденных и прямоугольных.
Пример 1. Решение:
Последняя строка полученной расширенной матрицы соответствует уравнению
далее, из второй строки получаем:
наконец, из первой строки:
Таким образом, система имеет единственное решение (1; -1; 2).
Пример 2. Решение. Поскольку ни один коэффициент в первом столбце не является единицей, что было бы удобно для обнуления остальных коэффициентов, мы можем предварительно получить нужную единицу, например, вычтя из первой строки расширенной матрицы вторую строку:
Это уравнение является тождеством при любых значениях переменных. Следовательно, мы не можем, как в предыдущем примере, определить из этого уравнения значение переменной z в решении системы. Она может принимать любые действительные значения: Далее, из второй строки:
и из первой строки:
Таким образом, система имеет бесконечно много решений вида
Пример 3. Решение.
последняя строка соответствует уравнению
ТЕМА II – ВЕКТОРНАЯ АЛГЕБРА И АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ §5. Векторы 5.1. Основные понятия
§ Рассмотрим направленный отрезок прямой на плоскости или в пространстве, пусть А – начальная точка этого отрезка, В – конечная точка. Такой отрезок называется вектором и обозначается Для того, чтобы задать вектор, необходимо указать: 1) прямую, на которой лежит вектор или которой он параллелен; 2) направление (ориентацию) вектора на этой прямой; 3) длину вектора. Один и тот же вектор может быть отложен от любой точки пространства при помощи параллельного переноса, при этом сохраняются все три указанные характеристики этого вектора. § Вектор называется нулевым, если его начало и конец совпадают: § Векторы § Векторы
§ Векторы Заметим, что от любой точки пространства можно отложить вектор § Три вектора
5.2. Операции над векторами § Суммой двух векторов
Из правила треугольника сложения векторов следует правило их вычитания: действительно, если § Произведением вектора § Любому ненулевому вектору Свойства: 1) 2) 3) 4) 5) Теорема 5.1. Векторы Пример. В треугольнике АВС точки M, N, K – середины сторон АВ, АС, ВС соответственно. Найти векторы
Далее, AK - половина диагонали параллелограмма, сторонами которого являются отрезки АВ и АС (так как диагонали параллелограмма точкой пересечения делятся пополам). Следовательно, по правилу параллелограмма сложения векторов, имеем
Рассмотрим трехмерное пространство. §
 , таких, что: , таких, что:
1) 2) 3) векторы В таком случае обычная декартова система координат соответствует заданному ортонормированному реперу, так что направления осей Ох, Оу, Oz совпадают с направлениями базисных векторов
§ Координатами вектора Отметим, что если вектор отложен от начала координат, то его координаты совпадают с координатами конца этого вектора.
Применив дважды правило параллелограмма, замечаем, что
§ Это соотношение называется разложением вектора Свойства: Пусть 1) 2) 3)
Теорема 5.2. Пусть точка А имеет координаты (xA, yA, zA), точка В(xВ, yВ, zВ). Тогда
Для доказательства достаточно заметить, что Замечание. Координаты вектора не изменятся, если этот вектор отложить от любой другой точки пространства. Доказательство этого факта предоставим читателю. Многие геометрические задачи на плоскости и в пространстве легко решаются с помощью векторов. При этом надо все условия задачи, сформулированные для точек и отрезков (а в дальнейшем – и углов) переформулировать для векторов, а затем перевести в координатную форму. Если рассматривается задача на плоскости, то и точки, и векторы имеют 2 координаты, и все сформулированные выше свойства имеют место для первых двух координат.
Пример 1: Точка М делит пополам отрезок АВ, где А(xA, yA, zA), В(xВ, yВ, zВ). Найти координаты точки М. Решение: Для решения этой задачи используем векторы.
Кроме того, по условию, Обозначим координаты точки М (xМ, yМ, zМ). Тогда Используя свойство 2) координат, имеем:
Пример 2. Даны точки: A(1; 0), B(4; 2), C(2; 5). Найти точку пересечения медиан треугольника АВС.
Найдем сначала координаты точек N и M как середин сторон АВ и АС (см. Пример 1). Точка М – середина отрезка АВ Þ Следовательно, можем найти координаты векторов:
Точка КÎСМ Û точка КÎBN Û Таким образом, мы получили два линейных уравнения с двумя неизвестными – координатами точки К. Решаем полученную систему:
Таким образом, искомая точка
§ Скалярным произведением двух векторов (где j - угол между векторами Свойства: 1) 2) 3) 4) 5) 6) Теорема 5.3. Пусть
Доказательство: Воспользуемся разложением векторов по базису и свойствами скалярного произведения:
Последнее равенство следует из того, что
Следствие. Замечание. Для векторов на плоскости, соответственно,
Пример 1. Найти угол между векторами
Решение:
Пример 2. Найти Решение: Используем свойства скалярного произведения:
Пример. Даны точки: А(-2; 1), В(3; 0), С(1; 4). Найти основание высоты треугольника АВС, проведенной из точки В.
BN – высота треугольника, то есть
Получили два линейных уравнения относительно координат:
Таким образом, искомая точка N(0; 3).
Векторное произведение § 1) 2) 3) векторы Свойства: 1) 2) 3) 4) 5) (геометрический смысл векторного произведения):
Теорема 5.4. Пусть
Доказательство аналогично доказательству соответствующей теоремы о скалярном произведении, с поправкой на свойства векторного произведения. Замечание. Для векторов на плоскости (с двумя координатами) векторное произведение не определено.
Пример. Даны векторы:
Рассмотрим параллелограмм ABCD, построенный на данных векторах. С одной стороны, как известно,
С другой стороны, воспользовавшись геометрическим смыслом векторного произведения, имеем: Найдем векторное произведение:
следовательно, Кроме того, найдем Таким образом,
Смешанное произведение § Смешанным произведением трех векторов Из свойств смешанного произведения особый интерес на практике представляет его геометрический смысл:
Следствие. Три ненулевых вектора компланарны тогда и только тогда, когда их смешанное произведение равно 0. Из определения смешанного произведения и теорем о вычислении скалярного и векторного произведений следует следующая теорема: Теорема 5.6. Пусть
Пример. Выяснить, лежат ли точки A(5; 7; -2), B(3; 1; -1), C(9; 4; -4), D(1; 5; 0) в одной плоскости. Решение: Данные точки будут лежать в одной плоскости в том и только том случае, если векторы
следовательно, данные точки лежат в одной плоскости.
§6. Аналитическая геометрия на плоскости 6.1. Уравнения прямых на плоскости Рассмотрим плоскость с заданной декартовой системой координат. ü Общее уравнение прямой
Ax+By+C=0 (А2+В2¹0). Это значит, что если точка плоскости принадлежит данной прямой, то ее координаты удовлетворяют уравнению этой прямой и наоборот, если два числа x и y удовлетворяют уравнению прямой, то точка с такими координатами принадлежит соответствующей прямой. В частности, если С=0, А¹0, В¹0, то прямая проходит через начало координат; если А=0, В¹0, С¹0, то прямая параллельна оси Ох; если В=0, А¹0, С¹0, то прямая параллельна оси Оy; ось Ох имеет уравнение y= 0; ось Оy имеет уравнение х= 0.
ü Уравнение прямой с угловым коэффициентом Пусть известно, что точка Р0(х 0, y 0) принадлежит прямой, а угол, образованный данной прямой с положительной полуосью Ох, равен a. Составим уравнение прямой. Пусть точка Р(х, y) – произвольная точка, принадлежащая данной прямой. Тогда рассмотрим прямоугольный треугольник
Коэффициент k называют угловым коэффициентом прямой, а точку Р0 – ее начальной точкой. ü Каноническое уравнение прямой Пусть точка Р0(х 0, y 0) – начальная точка прямой, а вектор
полученное уравнение называется каноническим уравнением прямой на плоскости. ü Если даны две точки Р1(x 1, y 1), P2(x 2, y 2), принадлежащие прямой, то в качестве направляющего вектора мы можем
ü Нормальное уравнение прямой Пусть Р0(х 0, y 0) – начальная точка прямой, а вектор Точка Р(х, y) принадлежит данной прямой тогда и только тогда, когда векторы
Полученное уравнение называется нормальным уравнением прямой.
ü Взаимное расположение прямых на плоскости Сравнивая различные виды уравнения прямой на плоскости, легко видеть, что, с точностью до постоянного множителя, А=n 1= v 2, B=n 2=- v 1. Пусть даны две прямые l 1: A 1 x+B 1 y+C 1 =0; l 2: A 2 x+B 2 y+C 2 =0. Тогда: а) l 1ïç l 2 Û б) l 1= l 2 Û в) (в частности, может быть В 1= А 2, В 2= - А 1); г) Точка пересечения прямых определяется системой линейных уравнений:
д) Угол между прямыми равен острому углу между их направляющими векторами, а также острому углу между их нормальными векторами.
Следовательно,
Пусть две прямые заданы уравнениями с угловыми коэффициентами: l 1: y=k 1 x+b 1; l 2 y=k 2 x+b 2. Тогда: а) l 1ïç l 2 Û k 1= k 2; б) l 1= l 2 Û k 1= k 2 и b 1= b 2; в) г) Решив совместно данные уравнения, получаем координаты точки пересечения прямых: д) Если
Пример. Дано общее уравнение прямой l: 2 x -5 y +6=0. 1) выяснить, лежит ли на данной прямой точка А(2; 2); 2) написать для прямой l уравнение с угловым коэффициентом; 3) написать уравнение прямой l 1, параллельной данной и проходящей через точку В(1; -3); 4) найти проекцию точки В на прямую l. Решение. 1) Точка А лежит на прямой l Û координаты точки А удовлетворяют уравнению прямой. Проверим: 2×2-5×2+6=0 – верно. Следовательно, точка А принадлежит данной прямой. 2) Для того, чтобы написать уравнение с угловым коэффициентом, выразим из данного общего уравнения у: 3) Из общего уравнения прямой l найдем координаты вектора
4) Сначала решим эту задачу на чертеже. Проведем через точку В прямую l 2, перпендикулярную прямой l и найдем пересечение прямых l и l 2.
Найденная точка N и будет искомой проекцией точки В на прямую l. Теперь проделаем те же действия в аналитической форме. Найдем уравнение прямой l 2. Поскольку
Найдем точку пересечения
Таким образом, искомая точка
|
|||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 137; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.139.238.76 (0.152 с.) |

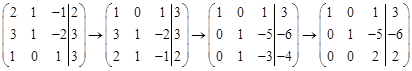
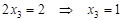 ;
;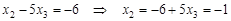 ;
; .
.
 Последняя строка полученной расширенной матрицы соответствует тривиальному уравнению:
Последняя строка полученной расширенной матрицы соответствует тривиальному уравнению: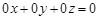 .
. . Заметим, что в таком случае эту переменную принято называть свободной.
. Заметим, что в таком случае эту переменную принято называть свободной. ,
,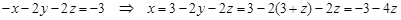 .
. .
.
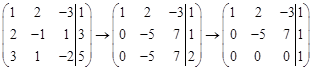
 , которое не является тождеством ни при каких значениях переменных. Следовательно, данная система не имеет решений, то есть противоречива.
, которое не является тождеством ни при каких значениях переменных. Следовательно, данная система не имеет решений, то есть противоречива.
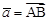 . Точки А и В называются началом и концом вектора соответственно. Длина отрезка АВ называется длиной или модулем вектора:
. Точки А и В называются началом и концом вектора соответственно. Длина отрезка АВ называется длиной или модулем вектора:  .
.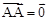
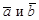 называются коллинеарными, если они лежат на параллельных или совпадающих прямых, обозначают
называются коллинеарными, если они лежат на параллельных или совпадающих прямых, обозначают 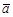 úï
úï 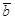 .
.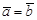 .
. называются компланарными, если они лежат в одной плоскости или в параллельных плоскостях.
называются компланарными, если они лежат в одной плоскости или в параллельных плоскостях. , построенный по правилу параллелограмма или треугольника:
, построенный по правилу параллелограмма или треугольника:
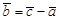 .
. , коллинеарный вектору
, коллинеарный вектору 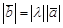 , который сонаправлен с вектором
, который сонаправлен с вектором 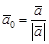 , имеющий единичную длину
, имеющий единичную длину  и направление которого совпадает с направлением вектора
и направление которого совпадает с направлением вектора 




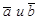 коллинеарны тогда и только тогда, когда
коллинеарны тогда и только тогда, когда  , если
, если  .
. Решение: По условию,
Решение: По условию, 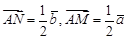 . Применяя правило вычитания, находим:
. Применяя правило вычитания, находим: ,
,  .
. .
. 5.3. Координаты векторов
5.3. Координаты векторов (единичные векторы),
(единичные векторы), (попарно перпендикулярные),
(попарно перпендикулярные), поворот от вектора
поворот от вектора 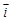 к вектору
к вектору 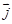 виден в положительном направлении – против часовой стрелки.
виден в положительном направлении – против часовой стрелки. Рассмотрим теперь произвольный вектор
Рассмотрим теперь произвольный вектор  в трехмерном пространстве.
в трехмерном пространстве.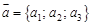 .
. .
. . Тогда
. Тогда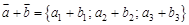

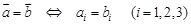
 4)
4) 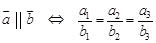
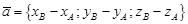 .
.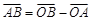 , причем
, причем 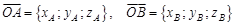 .
. Точка М лежит на отрезке АВ Û
Точка М лежит на отрезке АВ Û 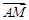 úï
úï 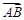 , причем эти векторы сонаправлены.
, причем эти векторы сонаправлены. . Следовательно,
. Следовательно, 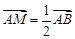 .
. ,
, 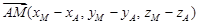 .
. , откуда выражаем
, откуда выражаем .
. Решение: Как известно, все медианы треугольника пересекаются в одной точке. Обозначим эту искомую точку К(xK, yK) и рассмотрим две медианы: BN и CM.
Решение: Как известно, все медианы треугольника пересекаются в одной точке. Обозначим эту искомую точку К(xK, yK) и рассмотрим две медианы: BN и CM. . Аналогично,
. Аналогично,  .
.
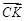 úï
úï  Û
Û 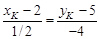 (свойство 4). Аналогично,
(свойство 4). Аналогично, úï
úï 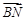 Û
Û  .
.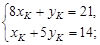 Þ
Þ 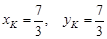 .
. .
.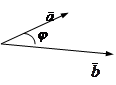 5.4. Скалярное произведение векторов
5.4. Скалярное произведение векторов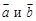 называется число
называется число 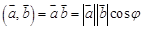
 для любых векторов
для любых векторов 
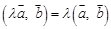 для любых векторов
для любых векторов 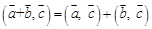 для любых векторов
для любых векторов 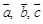

 (при этом считается, что нулевой вектор перпендикулярен любому)
(при этом считается, что нулевой вектор перпендикулярен любому) .
.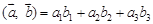 .
.

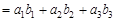 .
.
 (т.к.
(т.к. 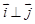 ) и т.п.
) и т.п.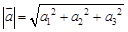 .
. и
и  .
.
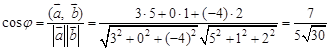 ,
, .
. .
. .
.
 .
.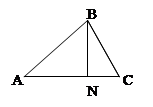 Решение: Точка N(xN, yN) Î АС Þ
Решение: Точка N(xN, yN) Î АС Þ  ïê
ïê  Þ
Þ  ;
;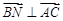 Þ
Þ 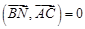 Þ
Þ  .
. Þ
Þ  .
.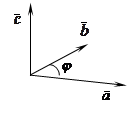 Векторным произведением двух векторов
Векторным произведением двух векторов 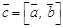 , определяемый следующим образом:
, определяемый следующим образом: , где j - угол между векторами
, где j - угол между векторами 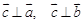
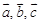 образуют правую тройку векторов.
образуют правую тройку векторов.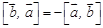 (антикоммутативность);
(антикоммутативность);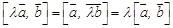 ;
;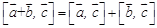
 Þ
Þ 
 модуль векторного произведения равен площади параллелограмма, построенного на векторах
модуль векторного произведения равен площади параллелограмма, построенного на векторах 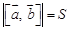

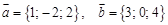 . Найти высоту параллелограмма, построенного на этих векторах, опущенную из конца вектора
. Найти высоту параллелограмма, построенного на этих векторах, опущенную из конца вектора 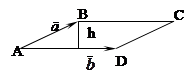 Решение:
Решение: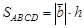 .
.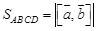 .
. ,
,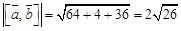 .
.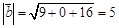
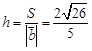 .
.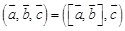 .
. Теорема 5.5. Модуль смешанного произведения трех ненулевых векторов
Теорема 5.5. Модуль смешанного произведения трех ненулевых векторов  .
.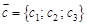 . Тогда
. Тогда 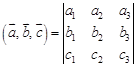 .
.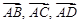 компланарны, что в свою очередь, равносильно утверждению, что смешанное произведение этих векторов равно 0. Проверим, так ли это.
компланарны, что в свою очередь, равносильно утверждению, что смешанное произведение этих векторов равно 0. Проверим, так ли это.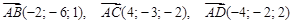 ;
;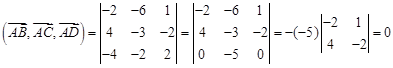 ,
, Утверждение. Любая прямая на плоскости описывается уравнением линии первого порядка:
Утверждение. Любая прямая на плоскости описывается уравнением линии первого порядка: Для того, чтобы написать уравнение прямой, можно использовать различные данные. Соответственно, получаются различные виды уравнения прямой (каждый из которых, тем не менее, можно привести к виду общего уравнения). Собственно, вывод уравнения прямой на плоскости и является доказательством сформулированного выше утверждения.
Для того, чтобы написать уравнение прямой, можно использовать различные данные. Соответственно, получаются различные виды уравнения прямой (каждый из которых, тем не менее, можно привести к виду общего уравнения). Собственно, вывод уравнения прямой на плоскости и является доказательством сформулированного выше утверждения.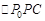 :
:
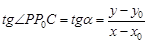 . Обозначив k= tga, получаем уравнение прямой в виде
. Обозначив k= tga, получаем уравнение прямой в виде y-y0=k(x-x0), или y =kx+b (b= y0+kx0)
y-y0=k(x-x0), или y =kx+b (b= y0+kx0) параллелен прямой (он называется ее направляющим вектором).
параллелен прямой (он называется ее направляющим вектором). Точка Р(х, y) принадлежит данной прямой тогда и только тогда, когда векторы
Точка Р(х, y) принадлежит данной прямой тогда и только тогда, когда векторы 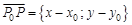 и
и  коллинеарны. Вспомнив свойства координат векторов, запишем это условие в координатной форме:
коллинеарны. Вспомнив свойства координат векторов, запишем это условие в координатной форме:

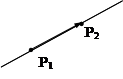 Уравнение прямой, проходящей через две точки:
Уравнение прямой, проходящей через две точки: выбрать вектор
выбрать вектор 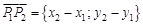 и записать каноническое уравнение:
и записать каноническое уравнение:
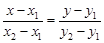
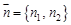 , перпендикулярен данной прямой (тогда его называют нормальным вектором).
, перпендикулярен данной прямой (тогда его называют нормальным вектором).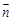 перпендикулярны, следовательно, их скалярное произведение равно нулю:
перпендикулярны, следовательно, их скалярное произведение равно нулю:
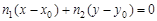 .
. (в частности, может быть А 1= А 2, В 1= В 2);
(в частности, может быть А 1= А 2, В 1= В 2);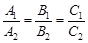 ;
;

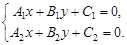
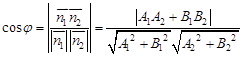
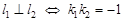 ;
;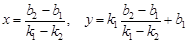 ;
; , то угол между прямыми
, то угол между прямыми 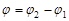 , следовательно:
, следовательно: .
. .
. . Пусть
. Пусть  , тогда
, тогда 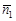 ïê
ïê  . В частности, можно считать, что
. В частности, можно считать, что  . Тогда запишем уравнение прямой l 1 с перпендикулярным вектором, проходящей через точку В: 2(х -1)-5(y +3)=0. Таким образом,
. Тогда запишем уравнение прямой l 1 с перпендикулярным вектором, проходящей через точку В: 2(х -1)-5(y +3)=0. Таким образом, l 1: 2 x -5 y- 17=0.
l 1: 2 x -5 y- 17=0. , то
, то 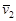 êê
êê 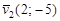 . Запишем уравнение прямой l 2, проходящей через точку В, с направляющим вектором:
. Запишем уравнение прямой l 2, проходящей через точку В, с направляющим вектором: , откуда получаем общее уравнение
, откуда получаем общее уравнение  .
.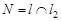 , решив систему уравнений
, решив систему уравнений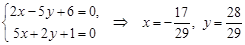
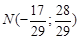 .
.


