
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Графический способ решения игр.
Задачу 2х2 можно решить графически. Возьмем участок оси абсцисс длиной 1 (см. рис. 1). Левый конец участка (точка с абсциссой х= 0) будет изображать стратегию А1; правый конец участка (х= 1) — стратегию А2. Проведем через точки А1 и А2 два перпендикуляра к оси абсцисс: ось I — I и ось II — II. На оси I — I будем откладывать выигрыши при стратегии А1, на оси II — II —выигрыши при стратегии А2.
Рассмотрим стратегию противника В1, она дает две точки на осях I — I и II — II с ординатами соответственно а11 и а21. Проведем через эти точки прямую В1В1. Очевидно, если мы при стратегии противника B1 будем применять смешанную стратегию, то наш средний выигрыш, равный в этом случае Очевидно, точно таким же способом может быть построена и стратегия В2 (см. рис. 2). Нам нужно найти оптимальную стратегию игрока А, т. е. такую, для которой минимальный выигрыш (при любом поведении В) обращался бы в максимум. Для этого построим нижнюю границу выигрыша при стратегиях B1 B2, т. е. ломаную B1NB2, отмеченную на рис. 2 жирной линией. Эта нижняя граница будет выражать минимальный выигрыш игрока А при любых его смешанных стратегиях; точка N, в которой этот минимальный выигрыш достигает максимума, и определяет решение и цену игры. Нетрудно убедиться, что ордината точки N есть цена игры v, а ее абсцисса равна р2 — частоте применения стратегии А2 в оптимальной смешанной стратегии игрока А.
В нашем случае решение игры определялось точкой пересечения стратегий. Однако это не всегда будет так; на рис. 3 показан случай, когда, несмотря на наличие пересечения стратегий, решение дает для обоих игроков чистые стратегии (А2 и В2), а цена игры v = a22 В данном случае матрица имеет седловую точку, и стратегия А1 является заведомо невыгодной, т. к. при любой чистой стратегии- противника она дает меньший выигрыш, чем А2.
В случае, когда заведомо невыгодная стратегия имеется у противника, геометрическая интерпретация имеет вид, представленный на рис.4.
В данном случае нижняя граница выигрыша совпадает со стратегией В1; стратегия В2 для противника является заведомо невыгодной. Геометрическая интерпретация дает возможность представить наглядно также нижнюю и верхнюю цены игры (рис. 5).
Мы убедились, что любая игра 2x2 может быть решена элементарными приемами. Совершенно аналогично может быть решена любая игра 2х n, где у нас имеются всего две стратегии, а у противника — произвольное число. Пусть мы располагаем двумя стратегиями: A1 A2, а противник — n стратегиями: B1,B2,...,Вn. Матрица || aij || задана; она состоит из двух строк и n столбцов. Аналогично случаю двух стратегий дадим задаче геометрическую интерпретацию; n стратегий противника изобразятся n прямыми (рис. 6). Строим нижнюю границу выигрыша (ломаную B1MNB2 и находим на ней точку N с максимальной ординатой. Эта точка дает решение игры; ордината точки N равна цене игры v, а абсцисса равна частоте р2 стратегии А2. В данном случае оптимальная стратегия противника получается применением смеси двух «полезных» стратегий: В2 и B4, пересекающихся в точке N. Стратегия В3 является заведомо невыгодной, а стратегия В1 —невыгодной при оптимальной стратегии игрока А. Если А будет придерживаться своей оптимальной стратегии, то выигрыш не изменится, какой бы из своих «полезных» стратегий ни пользовался В, однако, он изменится, если В перейдет к стратегиям В1 или В3. В теории игр доказывается, что у любой конечной игры m x n имеется решение, в котором число «полезных» стратегий той и другой стороны не превосходит наименьшего из двух чисел m и n.
В частности, из этого следует, что у игры 2 x m всегда имеется решение, в котором с той и другой стороны участвует не более двух, «полезных» стратегий. Пользуясь геометрической интерпретацией, можно дать простой способ решения любой игры 2 x m. Непосредственно но чертежу находим пару «полезных» стратегий противника Bj и Вk, пересекающиеся в точке N (если в точке N пересекается более двух стратегий, берем любые две из них). Мы знаем, что если игрок А придерживается своей оптимальной стратегии, то выигрыш не зависит от того, в какой пропорции применяет В свои «полезные» стратегии, следовательно, Зная цену игры, можно сразу определить оптимальную стратегию игрока В. Для этого решается, например, уравнение:
В случае, когда мы располагаем m стратегиями, а противник — всего двумя, очевидно, задача решается совершенно аналогичным способом; достаточно заметить, что, изменяя знак выигрыша на обратный, можно превратить игрока А из «выигрывающего» в «проигрывающего». Можно решить игру и без перемены знака выигрыша; тогда задача решается непосредственно для В, но строится не нижняя, а верхняя граница выигрыша (рис. 7). На границе ищется точка N с минимальной ординатой, которая и есть цена игры v.
|
||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 304; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.134.104.173 (0.006 с.) |
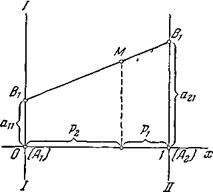 Рис. 1
Рис. 1 , изобразится точкой М на прямой В1В1; абсцисса этой точки равна р2. Прямую В1В1, изображающую выигрыш при стратегии B1 будем условно называть «стратегией B1».
, изобразится точкой М на прямой В1В1; абсцисса этой точки равна р2. Прямую В1В1, изображающую выигрыш при стратегии B1 будем условно называть «стратегией B1». Рис. 2.
Рис. 2. Рис. 3.
Рис. 3. Рис. 4.
Рис. 4. Рис. 5.
Рис. 5. Рис. 6.
Рис. 6. Из этих уравнений и условия
Из этих уравнений и условия  , находим р1, р2 и цену игры v.
, находим р1, р2 и цену игры v. , где
, где 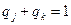 .
.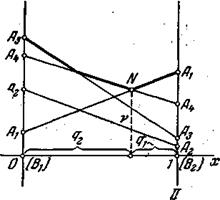 Рис. 7.
Рис. 7.


