
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Існування похідних всіх порядків аналітичної функції ⇐ ПредыдущаяСтр 4 из 4
1. Узагальнена формула Коші. Нехай дано функції
де точка
Маючи неповну інформацію про функцію Із (1.14) видно, що інтеграл який стоїть справа є аналітичною функцією змінної
З (1.15) видно, що інтеграл справа є теж аналітичною функцією, тому ми можемо знову диференціювати співвідношення (1.15):
…
Аналітичну функцію Розділ №2. Ряди аналітичних функцій Рівномірно збіжні функціональні ряди 1. Числові ряди. Сума вигляду Необхідною умовою збіжності ряду (2.1) є умова Згідно з ознакою Даламбера ряд вигляду Згідно з ознакою Коші ряд (2.2) збігається, якщо 2. Рівномірно збіжні функціональні ряди. Сума вигляду:
Якщо члени функціонального ряду є мажорованими членами збіжного числового ряду, то даний функціональний ряд (2.3) є рівномірно збіжним. Якщо (2.3) містить функції, які є аналітичними, і ряд є рівномірно збіжним, то його можна почленно диференціювати і інтегрувати:
Степеневі ряди. Ряд Тейлора 1. Теорема Абеля. Ряд вигляду Теорема Абеля. Нехай в точці
Із теореми Абеля випливають такі наслідки: 1) якщо в деякій точці 2) кожний степеневий ряд (2.4) має свій радіус збіжності 3) в середині круга збіжності радіусом
4) всередині круга збіжності радіусом 5) коефіцієнти ряду (2.4) можна виразити через його суму (тобто через функцію
6) вирази для знаходження радіусу збіжності степеневого ряду (2.4):
2. Ряд Тейлора. Теорема Тейлора. Нехай функція Доведення: Запишемо
Підставивши (2.6) і (2.7) у (2.5) отримаємо:
Це означає, що функцію
Єдність визначення аналітичної функції Користуючись єдністю подання функції у вигляді ряду Тейлора, можна показати, що: 1) якщо в області аналітичності функцій 2) якщо функції 3)
Аналітичне продовження Суть аналітичного продовження полягає в тому, якщо ми знаємо значення функції в деякій частині області аналітичності цієї функції, то ми можемо продовжити цю функцію (аналітично) на решту області аналітичності цієї функції. Частинний випадок: нехай ми маємо деяку функцію дійної змінної
Аналітичне продовження з дійсної вісі на комплексну площину, доцільно назвати так само. Властивості і співвідношення для функцій дійсної змінної переносяться на функції комплексної змінної завдяки тому, що аналітичне продовження є єдиним. Приклад: довести, що
Отже співвідношення, які існують для функцій дійсної змінної переносяться для функцій комплексної змінної, причому в тому ж самому вигляді. Це дає змогу перейти зокрема від диференціальних рівнянь стосовно функцій дійсної змінної до диференціальних рівнянь стосовно комплексної змінної, що в свою чергу може спростити процес розв'язування рівнянь.
Ряд Лорана 1. Означення і область збіжності ряду Лорана. Сума вигляду
Користуючись теоремою Абеля, з'ясовуємо, що частина ряду
Якщо об'єднати обидва співвідношення, для збіжності ряду Лорана, необхідно, щоб одночасно виконувались обидві умови:
2. Подання аналітичної функції у вигляді ряду Лорана. Теорема: Нехай функція
Доведення: Розглянемо деяку точку
Розглянемо другий доданок:
Розглянемо перший доданок:
Якщо об'єднати два доданки, то ми можемо записати єдиний вираз для коефіцієнтів ряду Лорана:
Отже, якщо функція
|
||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 201; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.87.156 (0.042 с.) |
 та
та  :
: , (1.13)
, (1.13)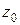 перебуває всередині контуру
перебуває всередині контуру 
 . (1.14)
. (1.14) , яка обмежена кривою
, яка обмежена кривою  з області
з області 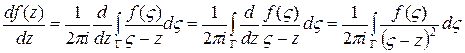 . (1.15)
. (1.15)

 (1.16), де
(1.16), де 
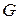 . Формула (1.16) називається узагальненою формулою Коші.
. Формула (1.16) називається узагальненою формулою Коші. (2.1) називається комплексним числовим рядом. Ряд (2.1) називається збіжним, якщо збігаються послідовності
(2.1) називається комплексним числовим рядом. Ряд (2.1) називається збіжним, якщо збігаються послідовності  його частинних сум
його частинних сум  . При цьому границя
. При цьому границя  послідовності
послідовності  .
.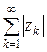 (2.2) є збіжним, якщо, починаючи з деякого номеру
(2.2) є збіжним, якщо, починаючи з деякого номеру  , відношення
, відношення 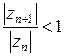 , для всіх
, для всіх  , а якщо починаючи з деякого номеру
, а якщо починаючи з деякого номеру  , то ряд (2.1) з комплексними членами розбігається.
, то ряд (2.1) з комплексними членами розбігається.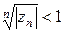 , для всіх
, для всіх 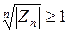 , то ряд (2.1) розбігається.
, то ряд (2.1) розбігається.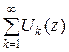 (2.3) називається функціональним рядом.
(2.3) називається функціональним рядом. , де
, де  ;
; .
.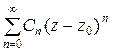 (2.4) називають степеневим рядом, де
(2.4) називають степеневим рядом, де  – коефіцієнти ряду,
– коефіцієнти ряду,  – елементи функціонального ряду.
– елементи функціонального ряду. степеневий ряд (2.4) є збіжним і
степеневий ряд (2.4) є збіжним і  , тоді цей ряд буде збіжним і для всіх точок
, тоді цей ряд буде збіжним і для всіх точок  , причому в крузі радіусом
, причому в крузі радіусом 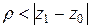 даний ряд буде рівномірно збіжним (без доведення).
даний ряд буде рівномірно збіжним (без доведення). ;
; ;
; ;
;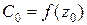 ,
,  ,
,  , …,
, …,  ;
; ,
,  .
. , тоді ця функція може бути подана у вигляді степеневого ряду
, тоді ця функція може бути подана у вигляді степеневого ряду  , причому такий ряд буде збіжним, а подання у вигляді цього ряду є однозначним, оскільки характеризується єдиним набором коефіцієнтів.
, причому такий ряд буде збіжним, а подання у вигляді цього ряду є однозначним, оскільки характеризується єдиним набором коефіцієнтів. , (2.5)
, (2.5) , (2.6)
, (2.6) ,
,  , (2.7)
, (2.7) .
. існує збіжна послідовність точок
існує збіжна послідовність точок  ,
,  ,…,
,…, 
 , і в цих точках
, і в цих точках 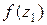 =
=  ,
,  =
=  ,…, то ці функції
,…, то ці функції 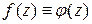 є тотожно рівними на всій області аналітичності цих функцій;
є тотожно рівними на всій області аналітичності цих функцій; , з області аналітичності цієї функції, є тотожно рівними на всій області
, з області аналітичності цієї функції, є тотожно рівними на всій області  ,
,  , то ці функції будуть співпадати у всіх точках області
, то ці функції будуть співпадати у всіх точках області  , яка є заданою на деякому проміжку
, яка є заданою на деякому проміжку  . Вважаючи, що
. Вважаючи, що  , то ми можемо аналітично продовжити цю функцію на комплексну площину. На підставі сказаного випливає, що така функція може бути тільки одна.
, то ми можемо аналітично продовжити цю функцію на комплексну площину. На підставі сказаного випливає, що така функція може бути тільки одна. :
:
 .
. (2.6) називається рядом Лорана. Для з'ясування області збіжності цього ряду розглянемо його у вигляді двох сум:
(2.6) називається рядом Лорана. Для з'ясування області збіжності цього ряду розглянемо його у вигляді двох сум:
 .
. має область збіжності внутрішню частину круга радіусом
має область збіжності внутрішню частину круга радіусом  . Розглянемо іншу частину ряду
. Розглянемо іншу частину ряду  і введемо заміну
і введемо заміну  , та отримаємо:
, та отримаємо:  . Даний ряд є степеневим із додатними степенями
. Даний ряд є степеневим із додатними степенями  , тому його збіжність буде також реалізуватись всередині круга радіусом
, тому його збіжність буде також реалізуватись всередині круга радіусом  .
. ,
, 

 .
. .
. ,
,  , причому
, причому  і
і  , та запишемо інтеграл Коші по кривих, які співпадають із колами
, та запишемо інтеграл Коші по кривих, які співпадають із колами  .
. :
:
 ,
,  , то відповідно:
, то відповідно: ,
,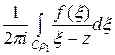 :
: ,
, ,
,  , то відповідно:
, то відповідно: .
. , де
, де  – довільний контур у коловому кільці.
– довільний контур у коловому кільці. .
.


