
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Справочные материалы для учащихся 9 класса.Стр 1 из 7Следующая ⇒
Справочные материалы для учащихся 9 класса.
Алгебра Натуральные числа и действия над ними Понятие натурального числа относится к простейшим, первоначальным понятиям математики и не определяется через другие, более простые понятия. Натуральные числа возникли в результате счета предметов. Их можно записывать как ряд чисел: 1, 2, 3,…Обозначается множество натуральных чисел N. Для натуральных чисел определены действия: сложение, вычитание, умножение, деление, возведение в степень, извлечение корня, причем сложение и умножение выполняются всегда. Результат сложения двух или нескольких чисел называется их суммой, а сами числа – слагаемыми: a + b + c + … + k = p, где p – сумма; a, b, c,…k – слагаемые. Законы: 1) a + b = b + a – переместительный, коммутативный; a · b = b · a 2) (a + b) + c = a + (b + c) – сочетательный, ассоциативный; (a · b) · c= a · (b · c) 3) (a + b) · c = a · c + b · c – распределительный, дистрибутивный. c · (a + b) = c · a + c · b Вычесть из числа а число b – значит найти такое число x, которое в сумме с числом b дает число a, т.е. a – b = x, если b + x = a, где x – разность a и b и обозначается a - b, a – уменьшаемое, b - вычитаемое. Разделить число a на число b – значит найти x, при умножении которого на число b получается a, т.е. a: b = x, если x · b = a, где a – делимое, b – делитель числа а, x – частное. Число, которое делится на 2, называется четным. Число, которое не делится на 2, называется нечетным. Признаки делимости чисел. 1. На 2 делятся все те, и только те числа, у которых в разряде единиц четное число. 2. На 5 делятся все те, и только те числа, у которых цифра единиц 0 или 5. 3. На 10 делятся числа, оканчивающиеся нулем. 4. На 3 (9) делятся те, и только те числа, сумма цифр которых делится на 3 (9). 5. На 4 (25) делятся те, и только те числа, у которых две последние цифры – нули, или выражают число, делящееся на 4 (25). 6. На 6 делятся те, и только те числа, которые делятся и на 2, и на 3. 7. Если каждое слагаемое делится без остатка на данное число, то и сумма разделится без остатка на данное число. 8. Если делятся на данное число все слагаемые, кроме одного слагаемого, которое не делится на данное число, то и сумма не разделится на данное число. 9. Если хотя бы один из сомножителей делится на данное число, то и все произведение разделится на данное число.
Простые и составные натуральные числа Если одно из натуральных чисел делится на другое без остатка, то первое число называется кратным второго, а второе – делителем первого. Например: 14: 7=2, 14 – кратное числа 7, а 7 – делитель числа 14; 14 – кратное числа 2, а 2 – делитель числа 14. Число a называется простым, если его делителями является только 1 и само число a. Например: 2, 3, 5, 13, 29,… Число a, имеющее более двух натуральных делителей (кроме 1 и a) называется составным. Например: 4, 6, 15,… Число 1 – ни простое, ни составное. Основная теорема арифметики. Любое составное натуральное число можно представить единственным образом в виде произведения простых чисел или их степеней Например: 110= 2 · 5 · 11; 12 = 2 · 2 · 3 = 22 · 3; 525 = 3 · 5 · 5 · 7 = 3 · 52 · 7.
Наибольший общий делитель (НОД) Число, на которое делится каждое из данных чисел, называется общим делителем этих чисел. Самый больший из общих делителей данных чисел называется их наибольшим общим делителем. Например: найти НОД чисел 126; 540; 630. Разложим эти числа на простые множители: 126= 2·3·3 ·7; 540=2· 2·3·3· 3·5; 630= 2·3·3 ·5·7. Найдем наибольший общий делитель 2·3·3=18. НОД(126, 540, 630)=18. Таким образом, чтобы найти НОД нескольких чисел, нужно разложить их на простые множители, выписать их общие простые множители и перемножить. Если наибольший общий делитель чисел равен 1, то такие числа называются взаимно простыми. Например: 16 и 25; НОД(16;25)=1, т.к. 16 = 2·2·2·2, 25 = 5·5.
Наименьшее общее кратное (НОК) Число, которое делится на каждое из данных чисел, называется общим кратным этих чисел. Самое меньшее из общих кратных данных чисел называется их наименьшим общим делителем. Например: найти НОК чисел 63; 280; 150. Разложим эти числа на простые множители: 63= 3·3 ·7; 280= 2·2·2·5·7; 150=2·3·5· 5. Найдем наименьшее общее кратное 2·2·2·3·3·5·5·7=12600. НОК(63;280;150)=12600. Таким образом, чтобы найти НОК нескольких чисел, необходимо разложить их на простые множители, из большего числа выписывают все множители и к ним приписывают недостающие множители из разложений остальных чисел. Если числа взаимно простые, то их произведение и есть НОК.
Периодические дроби Бесконечная десятичная дробь, в которой, начиная с некоторого разряда, цифры повторяются, называется периодической: 0,3333…=0,(3); 2,6555…=2,6(5). Любую обыкновенную дробь можно записать в виде либо конечной десятичной дроби, либо бесконечной периодической дроби. Правило перевода бесконечной периодической дроби в обыкновенную. Надо из числа, стоящего до второго периода, вычесть число, стоящее до первого периода, и записать эту разность числителем, а в знаменателе написать цифру 9 столько раз, сколько цифр в периоде, а после девяток дописать столько нулей, сколько цифр между запятой и первым периодом. Например: Правило перевода обыкновенной дроби в бесконечную периодическую дробь. Чтобы обратить обыкновенную дробь в десятичную, следует разделить числитель на знаменатель по правилу деления десятичной дроби на целое число. Например:
Целые числа Два числа, отличающиеся друг от друга только знаком, называются противоположными числами: 1 и -1, 2 и -2, 15 и -15,… Числа натуральные, им противоположные, а так же число нуль составляют множество целых чисел Z. Множество натуральных чисел, дополненное нулем, называется множеством целых неотрицательных чисел. Для целых чисел определены действия: сложение, вычитание, умножение, деление, возведение в степень, извлечение корня, причем сложение, вычитание и умножение выполняются всегда.
Рациональные числа Объединение множеств целых и дробных чисел (положительных и отрицательных) составляет множество рациональных чисел Q. Любое рациональное число На множестве рациональных чисел можно производить действия сложения, вычитания, умножения, деления (кроме деления на нуль).
Иррациональные числа Иррациональным числом называют бесконечную десятичную непериодическую дробь. Множество таких дробей составляет множество иррациональных чисел I. Например: 0,131331333125…; π ≈ 3,14; e ≈ 2,7;
Действительные числа Объединение множества рациональных чисел и множества иррациональных чисел даёт множество действительных чисел, которое обозначается R. Модуль числа Модулем (абсолютной величиной) действительного числа a называется само это число, если a≥ 0, и противоположное число –a, если a< 0. Модуль a обозначается | a |. Итак,
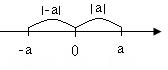
Геометрически | a | означает расстояние на координатной прямой от точки, изображающей число a, до начала отсчёта. Если a≠0, то на координатной прямой существуют две точки a и –a, равноудалённые от нуля, модули которых равны:
Свойства.
Числовые выражения Из чисел, знаков действий и скобок можно составить различные числовые выражения: Выполняя указанные в выражении действия, получим число, которое называется числовым значением или значением выражения. Если в выражении встречается деление на нуль, то выражение не имеет смысла. Два выражения называются тождественно равными, если при всех значениях, входящих в них переменных, принадлежащих общей области определений, соответственные значения этих выражений равны.
Одночлены. Многочлены Алгебраическое выражение, представляющее собой произведение чисел переменных и их степеней, называется одночленом: 3ax4; -2b; 0,5c3(-3b2).
Стандартным видом одночлена называется произведение, составленное из числового множителя (коэффициента) и степеней различных переменных: -2; а; 53; -9а5х3. Степенью одночлена стандартного вида называется сумма показателей степеней переменных. Например: 8х3у5 – степень одночлена равна 3+5=8; число 7 имеет нулевую степень, т.к. 7=7х0. Одночлены, отличающиеся только числовым коэффициентом или равные между собой, называются подобными. Сумму подобных членов можно заменить одним членом, сложив их коэффициенты и оставив ту же буквенную часть. Такое тождественное преобразование многочленов называют приведение подобных членов. Алгебраическая сумма одночленов называется многочленом. Например: 2а2-3ах5-6 – многочлен;
Если в многочлене все одночлены записаны в стандартном виде и приведены подобные члены, то полученный многочлен называется многочленом стандартного вида: 2х3у3+1,8ху4-3у+7. Степенью многочлена стандартного вида называется наибольшая степень одночлена, входящего в этот многочлен. Степень многочлена стандартного вида, рассмотренного ранее равна 3+3=6.
Неравенства и их свойства Запись, в которой два числа или два выражения, содержащие переменные, соединены знаком >, <, ≥, ≤ называется неравенством. Неравенства, составленные с помощью знаков >, < называются строгими; неравенства, составленные с помощью знаков≥, ≤, называются нестрогими. Два неравенства вида a > b и c > d называются неравенствами одинакового смысла; а вида a > b, c < d неравенствами противоположного смысла. Вместо двух неравенств x < a, a < y используется запись x < a < y – двойное неравенство. Неравенства, содержащие только числа, называются числовыми неравенствами. Решить неравенство, содержащее переменную, это значит найти множество значений переменной, при котором это неравенство является верным. Элементы этого множества называются решением неравенства. Два неравенства называются равносильными, если множества их решений совпадают. Свойства: 1. Если a > b, то b < a. 2. Если a > b и b > c, то a > c. 3. Если к обеим частям верного неравенства прибавить одно и то же число, то получим верное неравенство: a > b => a + c > b + c. 4. Если из одной части верного неравенства перенести в другую какое-либо слагаемое, переменив его знак на противоположный, то получим верное неравенство: a + b > c => a – c > -b.
5. Если обе части верного неравенства умножить на одно и то же положительное число, то получим верное неравенство: a > b, n > 0 => na > nb ( 6. Если обе части верного неравенства умножить на одно и то же отрицательное число и изменить знак неравенства на противоположный, то получим верное неравенство: a > b, n < 0 => na < nb ( 7. Неравенства одного смысла можно почленно складывать: a > b, c > d =>a + c > b + d 8. Неравенства противоположного смысла можно почленно вычитать: a > b, c < d => a - c > b - d 9. Если a > b > 0, c > d > 0 => ac > bd. 10. Обе части неравенства можно возводить в одну и ту же натуральную степень: a > b > 0, m 11. Из каждой части неравенства можно извлекать корень одной и той же натуральной степени: a > b > 0, m
Решение линейных неравенств Линейным неравенством называется неравенство вида Если a>0, то неравенство Если a<0, то неравенство
Например:
Свойства функции 1. Областью определения функции называются все значения переменной х, при которых функция имеет смысл (выполнимы указанные действия). 2. Множеством значений функции называются все значения переменной у. 3. Функция у = f(x) называется четной, если для любого значения х из области определения функции значение – х так же принадлежит области определения (область определения симметрична относительно начала отсчета) и выполняется равенство: f(-x) = f(x). График четной функции симметричен относительно оси ординат (оси Оу). Функция у = f(x) называется нечетной, если для любого значения х из области определения функции значение -х так же принадлежит области определения и выполняется равенство: f(-x) = -f(x). График нечетной функции симметричен относительно начала координат. 4. Нулем функции называется такое значение аргумента х из области определения функции, при котором значение функции равно 0. Для того, чтобы найти нули функции необходимо решить уравнение f(x) = 0. 5. Промежутки, на которых функция либо положительна, либо отрицательна, т.е. имеет один и тот же знак, называются промежутками знакопостоянства. 6. Функция называется периодической, если существует такое число Т ≠ 0, что для любого значения аргумента х из области определения значения х+Т и х–Т так же принадлежат области определения функции и выполняется равенство f(x) = f(x + T) = f(x - T). 7. Функция называется возрастающей на промежутке Х, если для любых х1 и х2 из этого промежутка, таких что х1 < х2, выполняется неравенство f(x1) < f(x2), т.е. большему значению аргумента соответствует большее значение функции. Функция называется убывающей на промежутке Х, если для любых х1 и х2 из этого промежутка, таких что х1 < х2, выполняется неравенство f(x1) > f(x2), т.е. большему значению аргумента соответствует меньшее значение функции. Возрастающая или убывающая на некотором промежутке функция называется монотонной. Промежутки, на которых функциявозрастает или убывает, называются промежутками монотонности.
8. Функция называется ограниченной снизу на некотором множестве Х, если существует такое действительное число М, что для каждого Функция называется ограниченной сверху на некотором множестве Х, если существует такое действительное число М, что для каждого Функция называется ограниченной на некотором множестве Х, если она ограничена и снизу, и сверху. 9. Наибольшим значением функции называется самое большое значение, которое принимает переменная у; наименьшим значением функции называется самое маленькое значение, которое принимает переменная у.
Арифметическая прогрессия Бесконечной числовой последовательностью называется функция, определенная на множестве натуральных чисел. Ее принято обозначать Числовая последовательность, каждый член которой, начиная со второго, равен предшествующему члену, сложенному с одним и тем же числом, называется арифметической прогрессией. Это число d называется разностью арифметической прогрессии. d = a2 – a1 = a3 – a2 = … = ak – ak-1 = … Арифметическая прогрессия задается своим первым членом a1 и разностью d. Любой член арифметической прогрессии можно вычислить по формуле (формула n-го члена) Если d > 0, то арифметическая прогрессия является возрастающей. Если d < 0, то арифметическая прогрессия является убывающей. Если d = 0, то все члены арифметической прогрессии равны между собой и она является постоянной последовательностью. Характеристическое свойство арифметической прогрессии. Числовая последовательность является арифметической прогрессией тогда и только тогда, когда каждый ее член, начиная со второго, является средним арифметическим предшествующего и последующего членов.
Сумма членов равноудаленных от концов прогрессии есть величина постоянная, т.е. Если на плоскости отмечать точки с координатами Это означает, что арифметическая прогрессия является линейной функцией, заданной на множестве натуральных чисел N и её можно задать формулой вида Сумма n – первых членов арифметической прогрессии вычисляется по формуле Доказательство: Запишем сумму n –первых членов арифметической прогрессии двумя способами.
Сложим почленно эти равенства.
В каждой скобке стоит сумма вида
Tаких скобок ровно n, тогда Геометрическая прогрессия Геометрической прогрессией называется числовая последовательность, в которой первый член отличен от нуля, а каждый последующий равен предыдущему, умноженному на некоторое постоянное для данной последовательности число не равное нулю. Это число называется знаменателем геометрической прогрессии Геометрическая прогрессия задается своим первым членом b1 и знаменателем q. Любой член геометрической прогрессии можно записать по формуле (формула n-го члена) Геометрическая прогрессия возрастает, если Геометрическая прогрессия убывает, если Если q < 0, то последовательность является ни возрастающей, ни убывающей, т.к. знаки ее членов чередуются. Характеристическое свойство геометрической прогрессии. Последовательность чисел является геометрической прогрессией тогда и только тогда, когда каждый ее член, начинается со второго, является средним геометрическим предыдущего и последующего членов Произведение членов, равноотстоящих от концов прогрессии, есть величина постоянная, т.е. Формула суммы n-первых членов геометрической прогрессии
Доказательство: Сумма n –первых членов геометрической прогрессии равна Если q = 1, то все члены равны b1, тогда Если q ≠ 1, то умножим равенство По определению геометрической прогрессии
Вычтем равенство (1) из равенства (2), получим
или Геометрическая прогрессия называется бесконечно убывающей, если |q| < 1. Суммой бесконечно убывающей геометрической прогрессии называется число, к которому стремится сумма ее n –первых членов при n→∞. Сумма S бесконечно убывающей геометрической прогрессии равна Справочные материалы для учащихся 9 класса.
Алгебра
|
||||||||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 172; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.204.208 (0.08 с.) |
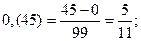
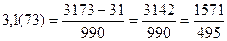 .
.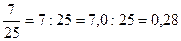 .
.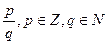 может быть представлено в виде конечной или бесконечной периодической десятичной дроби.
может быть представлено в виде конечной или бесконечной периодической десятичной дроби. и т.д.
и т.д.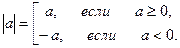
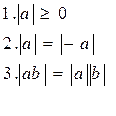


 - не многочлен.
- не многочлен.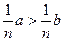 ).
). ).
).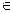 N => am > bm.
N => am > bm.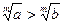 .
.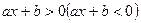 .
.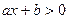 равносильно неравенству
равносильно неравенству 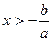 .
.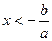 .
.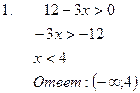

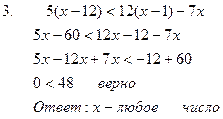
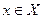 , f(x)
, f(x) 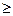 M.
M.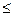 M.
M.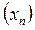 .
.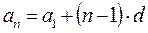 .
.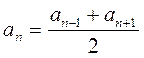 или
или  , где n, k
, где n, k 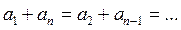 .
. , то, все эти точки будут лежать на графике функции, задаваемой формулой
, то, все эти точки будут лежать на графике функции, задаваемой формулой 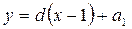 .
.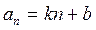 , где k, b – числа.
, где k, b – числа.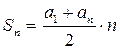 или
или 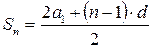 .
.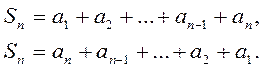
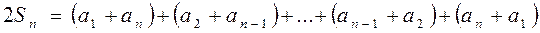
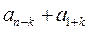 , где k = 0, 1, …, n-1.
, где k = 0, 1, …, n-1.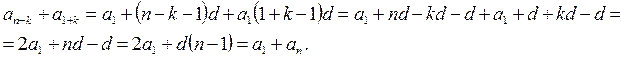
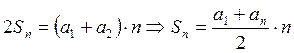 или
или 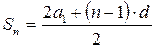 , что и требовалось доказать.
, что и требовалось доказать.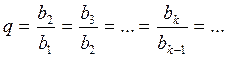 .
.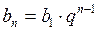 .
.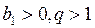 или
или 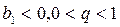 .
.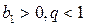 или
или  .
.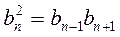 или
или 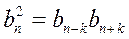 , где n, k
, где n, k 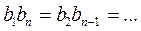 .
. , при q ≠ 1 и
, при q ≠ 1 и 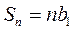 при q = 1.
при q = 1.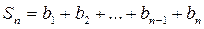 (1).
(1). – что и требовалось доказать.
– что и требовалось доказать.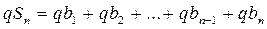 .
.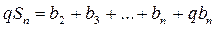 (2).
(2).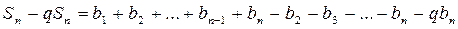 ;
; ;
; 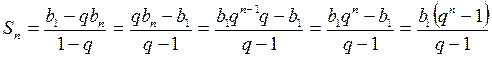
 , что и требовалось доказать.
, что и требовалось доказать. .
.


