
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Простейшие дифференциальные уравнения второго порядка.
Простейшее дифференциальное уравнение второго порядка имеет вид:
Решение таких уравнений сводится к решению дифференциальных уравнений первого порядка после введения вспомогательной функции Производная функции
Затем делаем обратную замену:
Пример. Решить дифференциальное уравнение второго порядка Решение. Введем вспомогательную функцию
Подставим начальные условия в полученное решение. Так как у(0)=2,то Частное решение исходного уравнения примет вид:
7.4.2. Дифференциальные уравнения второго порядка вида Решение уравнения данного вида можно найти с помощью вспомогательной функции
Пример. Решить дифференциальное уравнение второго порядка:
Решение. Преобразуем исходное дифференциальное уравнение: Найдем решение данного дифференциального уравнения.
Делаем обратную замену:
После интегрирования получим общее решение:
Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами. Определение: Линейным однородным дифференциальным уравнением второго порядка с постоянными коэффициентами называется уравнение вида:
Процедура решения таких дифференциальных уравнений состоит из следующих этапов:
1). Составляют характеристическое алгебраическое уравнение вида
2). Находят корни характеристического уравнения, от значения которых и зависит вид решения дифференциального уравнения.
Рассмотрим, какой вид имеет общее решение дифференциального уравнения второго порядка с постоянными коэффициентами при различных вариантах значений корней характеристического уравнения.
1). Корни характеристического уравнения действительные, разные и равные
2). Корни характеристического уравнения действительные, равные между собой
3). Если действительных корней характеристического уравнения нет, то говорят, что корни характеристического уравнения есть так называемые комплексные числа вида: При этом Тогда общее решение дифференциального уравнения записывают в виде:
Пример 1. Найти общее решение дифференциального уравнения:
Решение. Составим характеристическое уравнение:
Находим корни уравнения:
Общее решение имеет вид:
Пример 2. Найти частное решение дифференциального уравнения
Решение. Составим характеристическое уравнение Тогда общее решение дифференциального уравнения имеет вид:
Найдем частное решение при заданных начальных условиях. Подставим начальные условия в найденное решение:
Пример 3. Найти частное решение дифференциального уравнения
Решение. Составим характеристическое уравнение: Найдем корни характеристического уравнения: Значит, общее решение дифференциального уравнения имеет вид:
Дополним решение начальными условиями. Пусть Раздел 8. Понятие о рядах. Числовой ряд. Метод разложения в ряд является эффективным методом изучения функций. Он применяется для вычисления приближенных значений функций, для вычисления и оценок интегралов, для решения дифференциальных уравнений. Ряды бывают числовые и функциональные. Определение: Выражение вида:
Числовые ряды бывают сходящимися и расходящимися.
Ряд называется сходящимся, если последовательность частичных сумм Пример сходящегося ряда: Пример расходящегося ряда: (1+2+3…).
|
||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 1286; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.243.32 (0.014 с.) |
 , где А – некоторая постоянная.
, где А – некоторая постоянная. и подстановки ее в исходное уравнение.
и подстановки ее в исходное уравнение. равна
равна  . Подставим ее в исходное дифференциальное уравнение второго порядка и получим дифференциальное уравнение первого порядка с разделяющимися переменными, решение которого хорошо известно.
. Подставим ее в исходное дифференциальное уравнение второго порядка и получим дифференциальное уравнение первого порядка с разделяющимися переменными, решение которого хорошо известно.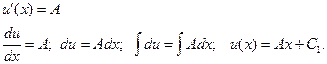
 И решаем это дифференциальное уравнение первого порядка обычным образом.
И решаем это дифференциальное уравнение первого порядка обычным образом.

 . Решаем его обычным образом:
. Решаем его обычным образом:
 . А так как
. А так как 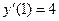 , то
, то  , значит
, значит  .
. .
. .
. . Последовательность действий при решении такова:
. Последовательность действий при решении такова: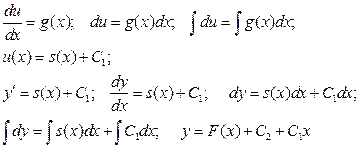
 .
. . Введем функцию
. Введем функцию  , тогда
, тогда 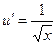 .
.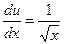 ,
, 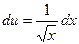 ,
, 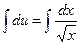 ,
, 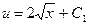 .
. , тогда
, тогда  ,
,  .
. .
.
 . В этом уравнении постоянные коэффициенты берут из исходного дифференциального уравнения второго порядка.
. В этом уравнении постоянные коэффициенты берут из исходного дифференциального уравнения второго порядка.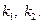 Запомним без доказательства, что в этом случае общее решение исходного дифференциального уравнения записывают в виде:
Запомним без доказательства, что в этом случае общее решение исходного дифференциального уравнения записывают в виде: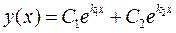
 . В этом случае общее решение имеет вид:
. В этом случае общее решение имеет вид: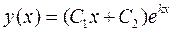
 , где α, β действительные числа, i – так называемая мнимая единица
, где α, β действительные числа, i – так называемая мнимая единица  .
. .
.
 .
. .
.

 .
.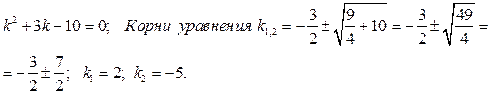



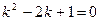 .
. , тогда
, тогда  .
.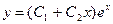 .
.
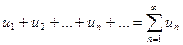 называется числовым рядом, а
называется числовым рядом, а - членами числового ряда, если они являются числами, для которых известен закон, позволяющий определить каждый элемент этого ряда.
- членами числового ряда, если они являются числами, для которых известен закон, позволяющий определить каждый элемент этого ряда. этого ряда имеет конечный предел:
этого ряда имеет конечный предел:  , где
, где 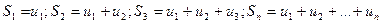 - частичные суммы ряда. В противном случае ряд является расходящимся.
- частичные суммы ряда. В противном случае ряд является расходящимся.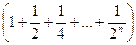 - геометрическая прогрессия.
- геометрическая прогрессия.


