
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Соотношение сторон в треугольникеСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Соотношение сторон в треугольнике всегда подчиняется следующему правилу: длина любой стороны треугольника не может быть больше суммы длин двух других сторон. Это правило так же называется теоремой о неравенстве треугольника. С помощью этой теоремы можно для любых трех сторон ответить на вопрос: можно ли из них построить треугольник? Пример 1. Существует ли треугольник со сторонами 3, 4, 5? Решение: Необходимо сравнить каждую сторону с суммой длин двух других. Возьмем сторону длиной 3. Тогда сумма длин двух других сторон равна: 4 + 5 = 9; 3 < 9. Возьмем сторону длиной 4. Тогда сумма длин двух других сторон равна: 3 + 5 = 8; 4 < 8. Возьмем сторону длиной 5. Тогда сумма длин двух других сторон равна: 3 + 4 = 7; 5 < 7. Во всех трех случаях правило выполняется, значит, треугольник со сторонами 3, 4, 5 существует. Пример 2. Существует ли треугольник со сторонами 9, 5, 2. Решение: Возьмем сторону длиной 9. Тогда сумма длин двух других сторон равна 5 + 2 = 7; 9 > 7. Правило не выполняется, значит, треугольник со сторонами 9, 5, 2 построить невозможно. Соотношение углов и сторон в треугольнике Для любого треугольника верно следующее: · Сумма углов треугольника равна 180°. · Напротив большего угла лежит большая сторона треугольника. · Напротив меньшего угла лежит меньшая сторона треугольника. По присутствующим углам в треугольнике выделяют: · остроугольные треугольники (содержат только острые углы); · прямоугольные треугольники (содержат один прямой угол); · тупоугольные треугольники (содержат один тупой угол). Зная длины всех сторон треугольника, всегда можно определить, к какому из перечисленных типов треугольника относится данный: · для прямоугольного треугольника выполняется равенство: а 2 + b 2 = c 2, где a, b ― катеты, а с ― гипотенуза; · для остроугольного треугольника для всех сторон выполняется неравенство: a 2 + b 2 > c 2; · для тупоугольного треугольника выполняется неравенство: a 2 + b 2 < c 2, где с ― сторона, лежащая против тупого угла. Пример: Докажите, что треугольник со сторонами 4, 5, 8 является тупоугольным. Решение: Т. к. тупой угол будет наибольшим в данном треугольнике, против него должна лежать наибольшая сторона, т. е. длиной 8. Проверим, будет ли выполняться неравенство a 2 + b 2 < c 2, где с – сторона, лежащая против тупого угла: 42 + 52 < 82; 16 + 25 < 64; 41 < 64. Неравенство выполняется, значит, данный треугольник является тупоугольным, причем против тупого угла лежит сторона, длиной 8. Особые треугольники Среди всех треугольников выделяют три особых треугольника: правильный, равнобедренный, прямоугольный. У таких треугольников есть ряд особых свойств. Равносторонний треугольник: · Все стороны равны. · Все углы равны 60°. · Биссектриса, проведенная из любого угла, является медианой и высотой. · Все биссектрисы/медианы/высоты пересекаются в одной точке ― в центре вписанной и описанной окружностей. Равнобедренный треугольник: · Боковые стороны равны. · Углы при основании равны. · Высота, проведенная из вершины, является медианой и высотой. Прямоугольный треугольник: · Для сторон выполняется теорема Пифагора: а 2 + b 2 = c 2, где a, b ― катеты, а с ― гипотенуза. · Медиана, проведенная из вершины прямого угла, равна половине гипотенузы. · Центр описанной окружности является серединой гипотенузы. · Соотношение сторон и углов лежит в основе тригонометрических функций: sin ― отношение противолежащего катета к гипотенузе; cos ― отношение прилежащего катета к гипотенузе; tg ― отношение противолежащего катета к прилежащему; ctg ― отношение прилежащего катета к противолежащему. Формулы для нахождения площади треугольника S = S = S = S = rp, где r ― радиус вписанной окружности, а p ― полупериметр. S =
Иррациональные уравнения Арифметический корень Пусть n — натуральное число, отличное от единицы, а — неотрицательное число.
Для арифметического корня n− й степени из неотрицательного числа а, используется обозначение По определению Для любых, в том числе отрицательных, значений а справедлива формула
|
|||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 9175; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.008 с.) |

 ah, где h ― высота, проведенная к стороне a.
ah, где h ― высота, проведенная к стороне a. , где R ― радиус описанной окружности.
, где R ― радиус описанной окружности.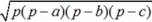 , где p ― полупериметр.
, где p ― полупериметр. . Если n = 2, пишут
. Если n = 2, пишут  .
. = a.
= a. = │ a │, в частности,
= │ a │, в частности,  = │ a │ и
= │ a │ и  =│ a − b │.
=│ a − b │.


