
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Декартово (прямое) произведение множеств
Вопрос29 Высказывание. Значение истинности высказывания. Отрицание. Коъюнкция. Дизъюнкция. Импликация. Эквиваленция высказываний. Логическая формула, таблица истинности для формулы. Свойства операций над высказываниями. Высказывание - повествовательное предложение, о котором можно говорить истинно оно или ложно. Отрица́ние в логике — унарная операция над суждениями, результатом которой является суждение (в известном смысле) «противоположное» исходному. Обозначается знаком перед или чертой над суждением. Синоним: логическое "НЕ". Конъю́нкция (от лат. conjunctio союз, связь) — логическая операция, по своему применению максимально приближённая к союзу "и". Синонимы: логи́ческое "И", логи́ческоеумноже́ние, иногда просто "И". Дизъю́нкция — (лат. disjunctio - разобщение) логическая операция, по своему применению максимально приближённая к союзу «или» в смысле «или то, или это, или оба сразу». Синонимы: логи́ческое «ИЛИ», включа́ющее «ИЛИ», логи́ческоесложе́ние, иногда просто «ИЛИ». Импликация — бинарная логическая связка, по своему применению приближенная к союзам «если … то …». Импликация записывается как посылка Суждение, выражаемое импликацией, выражается также следующими способами: Посылка является условием, достаточным для выполнения следствия; Следствие является условием, необходимым для истинности посылки. Эквивале́нция (или эквивале́нтность[1]) — двуместная логическая операция. Обычно обозначается символом ≡ или ↔. Задаётся следующей таблицей истинности:
Основные равносильности Закон двойного отрицания
Вопрос30. Предикат. Множество истинности предиката. Кванторы общности существования. Виды формулировок теорем (прямая и обратная теоремы, теорема о необходимых и достаточных условиях).
Предикат – выражение с логическими переменными, имеющие смысл при любых допустимых значениях этих пременных. Выражения: х > 5, x>y – предикаты.
Предика́т (n -местный, или n -арный) — это функция с множеством значений {0,1} (или «ложь» и «истина»), определённая на множестве Предикат называют тождественно-истинным и пишут:
если на любом наборе аргументов он принимает значение 1. Предикат называют тождественно-ложным и пишут:
если на любом наборе аргументов он принимает значение 0. Предикат называют выполнимым, если хотя бы на одном наборе аргументов он принимает значение 1. Ква́нтор — общее название для логических операций, ограничивающих область истинности какого-либо предиката. Чаще всего упоминают: Квантор всеобщности (обозначение: Квантор существования (обозначение:
Вопрос31 Граф и его элементы. Основные понятия. Инцидентность, кратность, петля, смежность. Типы графов. Маршрут в графе и его длина. Классификация маршрутов. Матрицы смежности ориентированного и неориентированного графов. граф — это совокупность непустого множества вершин и множества пар вершин. Объекты представляются как вершины, или узлы графа, а связи — как дуги, или рёбра. Для разных областей применения виды графов могут различаться направленностью, ограничениями на количество связей и дополнительными данными о вершинах или рёбрах. Путём (или цепью) в графе называют конечную последовательность вершин, в которой каждая вершина (кроме последней) соединена со следующей в последовательности вершин ребром. Циклом называют путь, в котором первая и последняя вершины совпадают. При этом длиной пути (или цикла) называют число составляющих его рёбер. Путь (или цикл) называют простым, если ребра в нём не повторяются; элементарным, если он простой и вершины в нём не повторяются. Несложно видеть, что: Всякий путь, соединяющий две вершины, содержит элементарный путь, соединяющий те же две вершины. Всякий простой неэлементарный путь содержит элементарный цикл. Всякий простой цикл, проходящий через некоторую вершину (или ребро), содержит элементарный (под-)цикл, проходящий через ту же вершину (или ребро).
Петля — элементарный цикл. Граф или неориентированный граф G — это упорядоченная пара G: = (V, E), для которой выполнены следующие условия: V это непустое множествовершин или узлов, E это множество пар (в случае неориентированного графа — неупорядоченных) вершин, называемых рёбрами. V (а значит и E, иначе оно было бы мультимножеством) обычно считаются конечными множествами. Многие хорошие результаты, полученные для конечных графов, неверны (или каким-либо образом отличаются) для бесконечных графов. Это происходит потому, что ряд соображений становится ложным в случае бесконечных множеств. Вершины и рёбра графа называются также элементами графа, число вершин в графе | V | — порядком, число рёбер | E | — размером графа. Два ребра называются смежными, если они имеют общую концевую вершину. Два ребра называются кратными, если множества их концевых вершин совпадают. Ребро называется петлёй, если его концы совпадают, то есть e = { v, v }. Степеньюdeg V вершины V называют количество инцидентных ей рёбер(при этом петли считают дважды). Вершина называется изолированной, если она не является концом ни для одного ребра; висячей (или листом), если она является концом ровно одного ребра. Ориентированный граф (сокращённо орграф) G — это упорядоченная пара G: = (V, A), для которой выполнены следующие условия: V это непустое множествовершин или узлов, A это множество (упорядоченных) пар различных вершин, называемых дугами или ориентированными рёбрами. Дуга — это упорядоченная пара вершин (v, w), где вершину v называют началом, а w — концом дуги. Можно сказать, что дуга Смешанный граф Смешанный граф G — это граф, в котором некоторые рёбра могут быть ориентированными, а некоторые — неориентированными. Записывается упорядоченной тройкой G: = (V, E, A), где V, E и A определены так же, как выше. Ориентированный и неориентированный графы являются частными случаями смешанного. Изоморфные графы (?) Граф G называется изоморфным графу H, если существует биекция f из множества вершин графа G в множество вершин графа H, обладающая следующим свойством: если в графе G есть ребро из вершины A в вершину B, то в графе H должно быть ребро из вершины f (A) в вершину f (B) и наоборот — если в графе H есть ребро из вершины A в вершину B, то в графе G должно быть ребро из вершины f − 1(A) в вершину f − 1(B). В случае ориентированного графа эта биекция также должна сохранять ориентацию ребра. В случае взвешенного графа биекция также должна сохранять вес ребра. Матрица смежности графа G с конечным числом вершин n (пронумерованных числами от 1 до n) — это квадратная матрица A размера n, в которой значение элемента aij равно числу рёбер из i -й вершины графа в j -ю вершину. Иногда, особенно в случае неориентированного графа, петля (ребро из i -й вершины в саму себя) считается за два ребра, то есть значение диагонального элемента aii в этом случае равно удвоенному числу петель вокруг i -й вершины. Матрица смежности простого графа (не содержащего петель и кратных ребер) является бинарной матрицей и содержит нули на главной диагонали.
Вопрос32 Функция. Способы задания. Классификация функций. Основные элементарные функции и их графики. Композиция функций. Элементарные функции.
Функция — математическое понятие, отражающее связь между элементами множеств. Можно сказать, что функция это «закон», по которому каждому элементу одного множества (называемому областью определения) ставится в соответствие некоторый элемент другого множества (называемого областью значений). Способы задания функции Аналитический способ Для задания функции пользуются выражением: Графический способ Числовые функции можно также задавать с помощью графика. Пусть Рассмотрим некоторое (n+1)-мерное линейное пространство над полем вещественных чисел (так как функция вещественная). Выберем в этом пространстве любой базис (
Линейная функция. графиком этой функциональной зависимости является прямая линия. Если C = 0, то она проходит через начало координат, в противном случае - нет. Графики линейных функций для различных комбинаций A, B, C показаны на рис.9.
Обратная пропорциональность. выражается уравнением:
y = k / x, где k - постоянная величина. График обратной пропорциональности – гипербола (рис.10 Квадратичная функция. Это функция: y = ax 2 + bx + c, где a, b, c - постоянные, a
Показательная функция. Функция y = ax, где a - положительное постоянное число, называется показательной функцией.
Логарифмическая функция. Функция y = log ax, где a – постоянное положительное число,не равное 1, называется логарифмической. Эта функция является обратной к показательной функции; её график (рис.18) может быть получен поворотом графика показательной функции вокруг биссектрисы 1-го координатного угла.
Тригонометрические функции. При построении тригонометрических функций мы используем радианную меру измерения углов.Тогда функция y = sin x представляется графиком (рис.19). Эта кривая называется синусоидой.
График функции y = cos x представлен на рис.20; это также синусоида, полученная в результате перемещения графика y = sin x вдоль оси Х влево на
Графики функций y = tan x и y = cot x показаны соответственно на рис.21 и рис.22
Композиция функций Если даны два отображения
Рис.1.30.Сквозное отображение
Вопрос33 Взаимно-однозначное соответствие между множествами. Обратное правило и обратная функция. Графики взаимно обратных функций. Определения, свойства и графики гиперболических функций. (тут уже начинается вынос мозга)
Множества A и B называют равномощными, если между их элементами можно установить взаимно однозначное соответствие (ещё говорят: можно установить взаимно однозначное отображение множеств). Мощность множества натуральных чисел обозначается א. Алеф א – первая буква еврейского алфавита, так обозначается наименьшая возможная для бесконечных множеств мощность.
Обратная функция.
1. Гиперболическими синусом, косинусом, тангенсом и котангенсом называются функции:
ch(x± y)=chx · chy ± shx · shy, (1) sh(x± y)=shx · chy± chx · shy, (2) ch2x–sh2x=1, (3) ch2x=ch2x+sh2x, (4) sh2x=2shx · chx. (5) Тождества (2) и (5) аналогичны соответствующим формулам тригонометрии, а формулы (1), (3) и (4) отличаются от тригонометрических только знаком. Доказываются тождества (1) – (5) непосредственной проверкой. Более подробно о тождествах для гиперболических функций изложено в разделе III.
2. Рассмотрим уравнение гиперболы:
Его можно записать в параметрическом виде, используя гиперболические функции (этим и объясняется их название). Обозначим y= b·sht, тогда х2 / а2=1+sh2t =ch2t. Откуда x=± a·cht.
Вопрос34. Числовая последовательность. Предел числовой последовательности (конечный и бесконечный). Геометрическая иллюстрация. Теорема о сходимости монотонной и ограниченной последовательности.
Последовательность — этопздц(набор) элементов некоторого множества: для каждого натурального числа можно указать элемент данного множества; Определение Пусть задано некоторое множество X элементов произвольной природы. Всякое отображение Образ натурального числа n, а именно, элемент xn = f (n), называется n -ымчленом или элементом последовательности, а порядковый номер члена последовательности — её индексом.
Предел числовой последовательности — это такое число, что для всякой сколь угодно малой величины существует номер, начиная с которого уклонение членов последовательности от данной точки становится меньше заранее заданной величины. Определение Число Частичный предел последовательности — это предел одной из её подпоследовательностей. Верхний предел последовательности — это наибольшая из её предельных точек. Нижний предел последовательности — это наименьшая из её предельных точек.
|
|||||||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 323; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.14.240.178 (0.084 с.) |






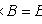

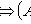

 следствие; применяются также стрелки другой формы и направленные в другую сторону (остриё всегда указывает на следствие).
следствие; применяются также стрелки другой формы и направленные в другую сторону (остриё всегда указывает на следствие).








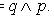


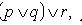




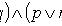

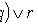


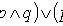






 . Таким образом, каждый набор элементов множества M характеризуется либо как «истинный», либо как «ложный».
. Таким образом, каждый набор элементов множества M характеризуется либо как «истинный», либо как «ложный».

 , читается: «для всех…», «для каждого…» или «каждый…», «любой…», «для любого…»).
, читается: «для всех…», «для каждого…» или «каждый…», «любой…», «для любого…»). , читается: «существует…» или «найдётся…»).
, читается: «существует…» или «найдётся…»). ведёт от вершины v к вершине w.
ведёт от вершины v к вершине w. . При этом, x есть переменная, пробегающая область определения функции, а y - область значений. Эта запись говорит о наличии функциональной зависимости между элементами множеств. х и y могут пробегать любые множества объектов любой природы.
. При этом, x есть переменная, пробегающая область определения функции, а y - область значений. Эта запись говорит о наличии функциональной зависимости между элементами множеств. х и y могут пробегать любые множества объектов любой природы. - вещественная функция n переменных.
- вещественная функция n переменных. ). Каждой точке функции сопоставим вектор:
). Каждой точке функции сопоставим вектор:  . Таким образом, мы будем иметь множество векторов линейного пространства, соответствующих точкам данной функции по указанному правилу. Точки соответствующего аффинного пространства будут образовывать некоторую поверхность.
. Таким образом, мы будем иметь множество векторов линейного пространства, соответствующих точкам данной функции по указанному правилу. Точки соответствующего аффинного пространства будут образовывать некоторую поверхность. 0. В простейшем случае имеем: b = c = 0 и y = ax 2. График этой функции квадратная парабола - кривая, проходящая через начало координат (рис.11
0. В простейшем случае имеем: b = c = 0 и y = ax 2. График этой функции квадратная парабола - кривая, проходящая через начало координат (рис.11
 /2.
/2.

 и
и  , где
, где  , то имеет смысл "сквозное отображение"
, то имеет смысл "сквозное отображение"  из
из  в
в  , заданное формулой
, заданное формулой  ,
,  , которое называется композицией функций
, которое называется композицией функций  и
и  и обозначается
и обозначается  .
.
 ;
;  ;
;  .
.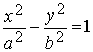
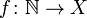 из множества натуральных чисел
из множества натуральных чисел  в заданное множество X называется последовательностью (элементов множества X).
в заданное множество X называется последовательностью (элементов множества X). называется пределом числовой последовательности
называется пределом числовой последовательности  , если последовательность
, если последовательность  является бесконечно малой, т. е. все её элементы, начиная с некоторого, по модулю меньше любого заранее взятого положительного числа.
является бесконечно малой, т. е. все её элементы, начиная с некоторого, по модулю меньше любого заранее взятого положительного числа.


