
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вычисление статических моментов и координат центра тяжести материальной кривой. ⇐ ПредыдущаяСтр 6 из 6
Статическим моментом точки относительно оси называется произведение массы точки на расстояние до прямой. Рассмотрим плоскую кривую, у которой плотность равна Пусть кривая задана уравнением Аналогично выводится формула для вычисления статического момента кривой относительно оси
Определение. Центр тяжести кривой Отсюда получаем формулы для нахождения координат центра тяжести однородной кривой В случае если кривая задана явно уравнением
Пример 1. Найти статический момент полуокружности относительно её диаметра.
Расположим полуокружность так, чтобы её диаметр находился на оси Уравнение верхней полуокружности
Пример 2. Найти статический момент относительно оси
Запишем параметрические уравнения астроиды
Формула для вычисления статического момента в случае, если кривая задана параметрическими уравнениями Вычислим подкоренное выражение
Подставив в формулу, находим значение статического момента
Найдем координаты центра тяжести В силу симметрии
Отсюда
Статические моменты и координаты центра тяжести плоских фигур
Рассматриваем случай, когда фигура является однородной, то есть ее плотность в каждой точке равна 1. Пусть фигура является криволинейной трапецией, ограниченной сверху графиком функции
Координаты центра тяжести
В случае явного задания функции уравнением
Пример 3. Найти статический момент относительно оси
Запишем параметрические уравнения циклоиды
Подставим эти уравнения в формулу для вычисления статического момента фигуры относительно оси
Найдем координаты центра тяжести фигуры. Так как Вычислим площадь фигуры
Учитывая, что соответствующий статический момент уже посчитан, находим ординату центра тяжести Теоремы Паппа-Гульдина
Впервые эти теоремы нашел александрийский математик Папп в 3 веке н.э. В эпоху средневековья многие достижения античной науки были в Европе утрачены. В 17-ом веке теоремы вновь открыл швейцарский математик Гульдин.
Первая теорема Паппа-Гульдина. Площадь поверхности, образованной вращением кривой вокруг не пересекающей её оси, равна произведению длины кривой на путь, проходимый центром тяжести этой кривой. В случае вращения вокруг оси
Доказательство. Рассмотрим случай плоской кривой, когда она задана явно уравнением
Затем домножим обе части этого равенства на
В правой части этого равенства стоит площадь поверхности тела, образованного вращением кривой вокруг оси В левой части равенства стоит произведение длины кривой Пример 1. Найти координаты центра тяжести полуокружности радиуса
Пример 2. Найти площадь поверхности вращения полуокружности вокруг касательной, параллельной её диаметру.
Тогда радиус окружности, описываемой центром тяжести при вращении полуокружности вокруг касательной, равен
Вторая теорема Паппа-Гульдина. Объём тела, образованного вращением плоской фигуры вокруг не пересекающей её оси, равен произведению площади фигуры на путь, проходимый центром тяжести этой фигуры. В случае вращения вокруг оси
Доказательство. Рассмотрим случай плоской кривой, когда она задана явно уравнением
В правой части стоит объем тела, полученного вращением кривой вокруг оси Теорема доказана.
Пример 3. Найти координаты центра тяжести полукруга радиуса R с центром в начале координат, расположенного в верхней полуплоскости.
Воспользуемся второй теоремой Паппа-Гульдина. При вращении вокруг оси
|
||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 2160; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.104.238 (0.017 с.) |

 , тогда масса кривой равна ее длине, найдём статический момент кривой относительно оси
, тогда масса кривой равна ее длине, найдём статический момент кривой относительно оси  .
.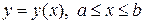 . Возьмем на кривой точку
. Возьмем на кривой точку  и вырежем из кривой элементарный участок длины
и вырежем из кривой элементарный участок длины  , содержащий точку
, содержащий точку  . Тогда статический момент всей кривой относительно оси
. Тогда статический момент всей кривой относительно оси  .
. :
:  .
.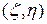 – это такая точка, что если в ней сосредоточить всю массу кривой, то ее статический момент относительно оси, не пересекающей кривую, будет равен статическому моменту всей кривой:
– это такая точка, что если в ней сосредоточить всю массу кривой, то ее статический момент относительно оси, не пересекающей кривую, будет равен статическому моменту всей кривой: 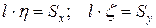 .
. .
. , координаты центра тяжести кривой находятся по формулам
, координаты центра тяжести кривой находятся по формулам .
. . Найдем значение подкоренного выражения в формуле для вычисления статистического момента
. Найдем значение подкоренного выражения в формуле для вычисления статистического момента  . Подставляя в формулу, получаем ответ
. Подставляя в формулу, получаем ответ  .
.
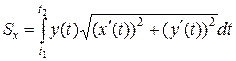 .
. .
. .
.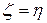 . Найдем ординату центра тяжести по формуле
. Найдем ординату центра тяжести по формуле , где
, где  .
. .
. . Для определения соответствующих элементарных моментов предположим всю массу полоски сосредоточенной в ее центре тяжести, то есть центре прямоугольника. Полученная материальная точка отстоит от оси
. Для определения соответствующих элементарных моментов предположим всю массу полоски сосредоточенной в ее центре тяжести, то есть центре прямоугольника. Полученная материальная точка отстоит от оси  , от оси
, от оси 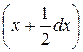 , что приближенно равно
, что приближенно равно  . Тогда элементарные моменты равны
. Тогда элементарные моменты равны  и
и  . Отсюда получаем формулы
. Отсюда получаем формулы ;
;  .
. однородной криволинейной трапеции определяются по формулам
однородной криволинейной трапеции определяются по формулам  .
. .
.

 , то фигура симметрична относительно прямой
, то фигура симметрична относительно прямой  . Поэтому абсцисса центра тяжести
. Поэтому абсцисса центра тяжести 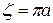 . Ординату центра тяжести находим по формуле
. Ординату центра тяжести находим по формуле  .
.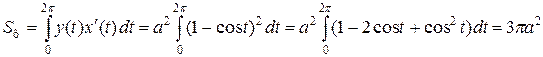 .
.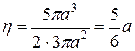 . Итак, центр тяжести фигуры расположен в точке
. Итак, центр тяжести фигуры расположен в точке  .
. .
. , получаем
, получаем .
. :
: .
.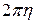 , которую описывает центр тяжести. Теорема доказана.
, которую описывает центр тяжести. Теорема доказана.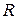 с центром в начале координат, расположенной в верхней полуплоскости.
с центром в начале координат, расположенной в верхней полуплоскости. В силу симметрии абсцисса центра тяжести
В силу симметрии абсцисса центра тяжести  . Найдем ординату центра тяжести, используя первую теорему Паппа-Гульдина. Поверхность, образованная при вращении кривой вокруг оси
. Найдем ординату центра тяжести, используя первую теорему Паппа-Гульдина. Поверхность, образованная при вращении кривой вокруг оси  . Длина кривой равна половине длины окружности
. Длина кривой равна половине длины окружности  . Подставив эти значения в формулу
. Подставив эти значения в формулу  , найдем ординату центра тяжести
, найдем ординату центра тяжести  .
. Используем результат, полученный в предыдущем примере. Ордината центра тяжести полуокружности
Используем результат, полученный в предыдущем примере. Ордината центра тяжести полуокружности  .
. . Из первой теоремы Паппа-Гульдина имеем формулу
. Из первой теоремы Паппа-Гульдина имеем формулу 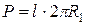 . Отсюда искомая площадь поверхности
. Отсюда искомая площадь поверхности .
. .
. . Применяя формулу для вычисления статического момента
. Применяя формулу для вычисления статического момента  , получаем
, получаем  . Домножим на число
. Домножим на число  .
. , площадь полукруга равна
, площадь полукруга равна 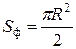 . Подставляя эти значения в формулу
. Подставляя эти значения в формулу  .
.


