
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Усунення кон'юнктивного члена
Цей метод гарний тим, що взявши за умову продовження циклу усунений кон'юнктивний член, ми автоматично добиваємося істинності четвертого пункту теореми 10.1, яка гарантує правильність побудованого циклу.
Рішення. Побудуємо інваріант за допомогою методу усунення кон'юнктивного члена Умовою продовження циклу e може бути заперечення видаленого кон'юнктивного члена: Для того щоб цикл завершився, величина а повинна збільшуватися. Найпростіший спосіб - збільшувати а на одиницю на кожній ітерації циклу. Легко помітити, що це перетворення зберігає інваріант, тому побудову програми завершено. Перший варіант програми буде строго відповідати її специфікації. Текст програми. Фрагмент програми
int a, n = Xterm.inputInt ("n ->");
1)
2) Тому
Істинність першого кон'юнктивній члена випливає з припущення про істинність
Застосуємо метод усунення кон'юктивного члена для побудови інваріанта циклу при вирішенні ще одного завдання. ЗАВДАННЯ 10.2. Напишіть програму (лінійний пошук), яка визначає перше входження заданого цілого числа x в заданий масив
Рішення. Випишемо формально задані нам перед- і післяумови:
Враховуючи те, що домогтися істинності третього кон'юнктивного члена одним або кількома простими присвоювання важко, усунемо саме його. Тоді отримаємо Обмежуючою функцією можна спробувати взяти Зрозуміло, що збільшуючи і більше, ніж на одиницю, можна пропустити перше входження Текст програми.
"i + = 1;"
, тому
Дана імплікація є тавтологією, бо якщо в під масиві
S;"., h<h1))=(I∧e⇒T)=(!I⋁!e⋁T)=T
Як перший приклад використання цього методу побудови інваріанта розглянемо просту задачу сумовування елементів масиву. Задача 2.3. Напишіть програму, що знаходить суму s елементів заданого цілочисельного масиву
Розв'язання. У післяумову входить константа
Істинності інваріанта легко домогтися обнуленням величин Для того, щоб цикл завершився, необхідно зменшувати h, що цілком природно робити, збільшуючи i на одиницю на кожній ітерації циклу. Використовуючи інваріант, знаходимо, що другим необхідною дією є додавання до s значення b[i]: Текст програми. public class SumArr {staticint b[];public static void main(String[] args) throws Exception { int n = Xterm.inputInt("n -> ");b = new int[n]; for (int k=0; k<n; k++)b[k] = Xterm.inputInt("b["+k+"] -> ");inti=0, s=0;while (i< n) { s += b[i]; i += 1; }Xterm.println("s = " + s); }}Доведемо її правильність. 1) Враховуючи, що wp("i=0;s=0;",
то 2)
Тепер обчислимо.
Даний предикат свідомо істинний, якщо правдивий один з перших чотирьох його диз'юнктивних членів. В іншому випадку маємо 3). Очевидно, що
5) Отже Побудуємо більш швидку програму знаходження наближеного значення квадратного кореня. Задача 2.4. Напишіть програму, що знаходить наближене значення квадратного кореня Розв'язання. Побудуємо інваріант за допомогою методу заміни константи Після присвоювань "a = 0; b = n + 1;" предикат 𝐼 стає істинним, отже наша програма має вигляд "a = 0; b = n + 1; while (a + 1! = b) S;" з невідомих поки тілом циклу S. Для того щоб цикл завершився, необхідно зменшуватись h, що еквівалентно зближенню чисел 𝑎 і 𝑏. Зменшення різниці 𝑏-𝑎 на одиницю на кожній ітерації циклу не дозволить досягти необхідної b умові задачі ефективності програми. Потрібна тимчасова складність може бути отримана при використанні методу ділення відрізка [a, b] навпіл на кожній ітерації і виборі тієї з половинок, на якій лежить шукане наближене значення квадратного кореня. Реалізація даної ідеї призводить до наступній програмі. Текст програми. publicclassSqrt3 {public static void main(String[] args) throws Exception {int a, b, n; n = Xterm.inputInt("n -> "); a = 0; b = n+1;while (a+1!= b) {int c = (a+b)/2;if (c*c <= n) a = c;else b = c; } Xterm.println("sqrt(" + n + ") = " + a);}}Доведіть самостійно її правильність та оцініть ефективність.
|
||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 270; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.161.116 (0.017 с.) |
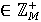 із заданого невід'ємного цілого числа
із заданого невід'ємного цілого числа  . Ось більш точне формулювання перед- і постумови:
. Ось більш точне формулювання перед- і постумови: 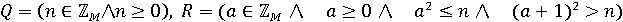 При написанні програми величину
При написанні програми величину  з післяумови
з післяумови 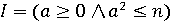 .
. , що еквівалентно вибору обмежуючої функції
, що еквівалентно вибору обмежуючої функції 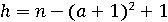 . Істинність інваріанта перед початком виконання циклу легко встановлюється присвоюванням "a = 0;" і нам залишається тільки зрозуміти, як реалізувати тіло циклу
. Істинність інваріанта перед початком виконання циклу легко встановлюється присвоюванням "a = 0;" і нам залишається тільки зрозуміти, як реалізувати тіло циклу 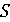 .
.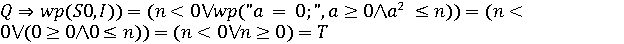
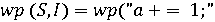
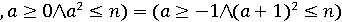 ,
,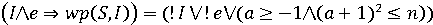 .
.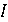 або
або  , у протилежному випадку він легко спрощується:
, у протилежному випадку він легко спрощується: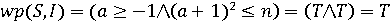 .
.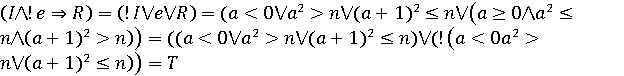 .
.
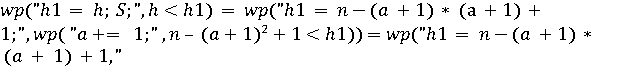 ,
, 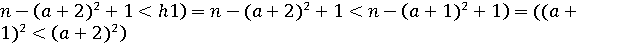 , в припущенні, що правдиві
, в припущенні, що правдиві 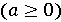 .
. .
.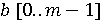 цілих чисел
цілих чисел 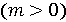 . Відомо, що
. Відомо, що 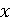 знаходиться в масиві b. Значення елементів масиву b і число x в програмі змінювати не можна.
знаходиться в масиві b. Значення елементів масиву b і число x в програмі змінювати не можна.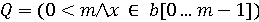
 .
.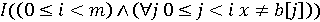 . Умовою продовження циклу можна взяти заперечення видаленого члена
. Умовою продовження циклу можна взяти заперечення видаленого члена 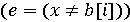 , а інваріант легко зробити істинним, виконуючи команду "i = 0;", тому програма повинна мати вигляд "i = 0; while (x! = b [i]) S; " з невідомим нам поки S.
, а інваріант легко зробити істинним, виконуючи команду "i = 0;", тому програма повинна мати вигляд "i = 0; while (x! = b [i]) S; " з невідомим нам поки S.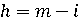 , a для того, щоб вона зменшувалася, досить збільшувати
, a для того, щоб вона зменшувалася, досить збільшувати 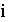 на кожній ітерації циклу.
на кожній ітерації циклу. , що випливає з
, що випливає з 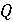 .
.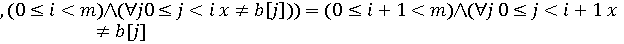
 .
. елемент
елемент 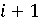 в масиві
в масиві 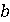 завідомо є (тобто I + 1 < m).
завідомо є (тобто I + 1 < m).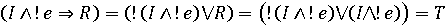
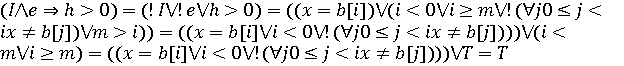
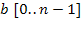 , елементи якого і величину n змінювати не можна. Точні перед- і пост умови:
, елементи якого і величину n змінювати не можна. Точні перед- і пост умови: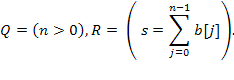
 , яку ми можемо замінити новою змінною i, що змінюється в діапазоні від 0 до
, яку ми можемо замінити новою змінною i, що змінюється в діапазоні від 0 до 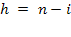 .
.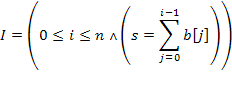
 і s, тому шукана програма буде мати вигляд "i = 0; s = 0; while (i <n) S;" з невідомим нам поки тілом циклу S.
і s, тому шукана програма буде мати вигляд "i = 0; s = 0; while (i <n) S;" з невідомим нам поки тілом циклу S.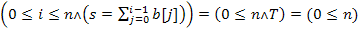 ,
,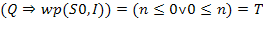 .
.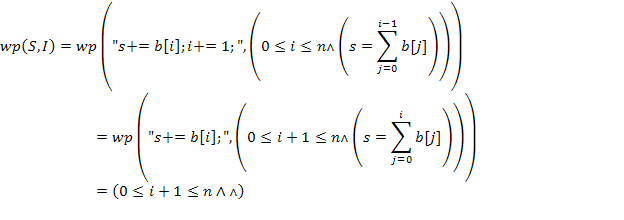
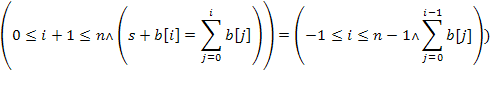
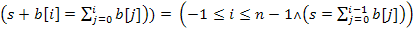 .
.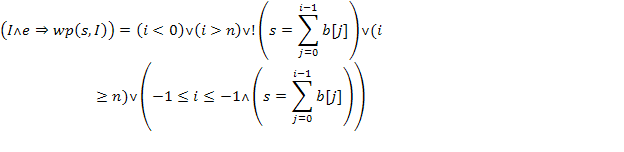
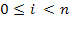 і
і  , тому правдивий п'ятий його диз'юнктивний член, отже предикат є тавтологією.
, тому правдивий п'ятий його диз'юнктивний член, отже предикат є тавтологією.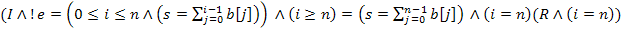
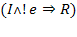 .
. .
.

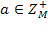 із заданого невід'ємного числа n. Точні перед- і постумови необхідної програми, тимчасова складність якої не повинна перевершувати
із заданого невід'ємного числа n. Точні перед- і постумови необхідної програми, тимчасова складність якої не повинна перевершувати  такі:
такі: 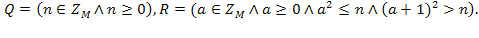 При написанні програми величину n змінювати не можна.
При написанні програми величину n змінювати не можна.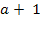 на змінну b. З умови задачі випливає, що
на змінну b. З умови задачі випливає, що 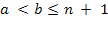 , отже інваріантом є предикат
, отже інваріантом є предикат  . Умова продовження циклу легко виходить з того факту, що предикат
. Умова продовження циклу легко виходить з того факту, що предикат 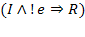 повинен бути тавтологією
повинен бути тавтологією  , а це означає використання обмежуючій функції
, а це означає використання обмежуючій функції 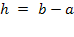 .
.


