
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Уравнение движения в координатах Эйлера и координатах Лагранжа. ⇐ ПредыдущаяСтр 3 из 3
При построении нелинейной теории ЭП с продольным взаимодействием и для использования МКЧ введем ряд приближений в теории: - рассматриваем нерелятивистский случай и пренебрегаем собственным магнитным полем электронов; - рассматриваем случай бесстолкновительных электронных пучков и считаем, что поток в целом нейтрален; - используем квазистатическое приближение, т.е. пренебрегаем эффектами запаздывания и вместо решения уравнений Максвелла будем решать уравнение Пуассона для потенциала объемного заряда; - считаем справедливым квазипериодическое приближение; - будем использовать одномерное приближение и в аксиально- симметричном случае в роли крупных частиц будем использовать жесткие заряженные диски с конечными размерами. Учитывая введенные приближения, уравнение электронного пучка в координатах Эйлера имеет следующий вид:
где e, m и В подходе Эйлера электронный пучок представляется в виде сплошной заряженной жидкости и за движением сплошной среды происходит наблюдение в определенных точках физического пространства. Координаты точек наблюдения являются независимыми эйлеровыми координатами z, t. В подходе Лагранжа происходит наблюдение за движением отдельных выбранных частиц и совокупность фазовых траекторий этих частиц дает полную информацию о процессе. Независимыми переменными в подходе Лагранжа являются номера частиц или их начальные фазовые координаты- z, t 0. Время t становится зависимой переменной t=t (z, t 0). Запишем уравнение движения (19) в новых лагранжевых координатах:
где Более удобно в дальнейшем использовать фазовую систему координат Лагранжа, которая вводится следующими соотношениями: y=ebez, Ф=wt-bez, (21) где e - параметр малости, эквивалентный коэффициенту усиления C в теории ЛБВ, Уравнение движения (20) в фазовой системе координат принимает следующий вид:
где
Расчет кулоновских сил. Расчет сил пространственного заряда электронного пучка является наиболее сложной задачей нелинейной теории. Будем использовать приближение эквивалентного гладкого волновода, приближение узких зазоров для многорезонаторных клистронов, квазистатическое и квазипериодическое приближения в МКЧ.
В нелинейной теории ЭП применяются различные методы расчета поля пространственного заряда, из которых наиболее распространены следующие: метод функций Грина, метод преобразования Фурье и метод конечных разностей. Нами в данной работе будет использоваться метод функций Грина. Продольная составляющая электрического поля Ez в правой части уравнения движения состоит из двух слагаемых - Ezл - поля замедляющей системы и Ezе - собственного поля электронного пучка (кулоновское поле или поле сил пространственного заряда). В квазистатическом приближении для определения собственного электрического поля необходимо решить уравнение Пуассона Dj = -r / e 0 и найти потенциал j квазистатического электромагнитного поля, после чего определяется кулоновское поле Eze=-grad j, где r - плотность заряда электронного пучка, e 0 - диэлектрическая постоянная активной среды. Из электродинамики известно решение уравнения Пуассона для эквивалентной гладкой трубы дрейфа, в которой движется электронный поток, выражаемое с помощью функции Грина. Поэтому мы сразу выпишем готовое решение для кулоновского поля
где f (z,z’) - это усредненная функция Грина (функция влияния), описывающая действие кулоновских сил со стороны диска в сечении z на диск в сечении z’, Eze- усредненная напряженность электрического поля, действующая на сечение z’ со стороны всех других сечений пучка слева и справа. Запишем аналитическое выражение для усредненной функции Грина, представляемой в виде экспоненциальной функции,
где rп - радиус электронного пучка,
Перейдем во введенную нами ранее фазовую систему координат Лагранжа, тогда соотношение (24) для усредненной функции Грина в движущейся системе координат вместе с электронным потоком примет следующий вид:
где k=2/berп - параметр убывания кулоновских сил с расстоянием, используемый в нелинейной теории, DФ=Ф-Ф’.
|
||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 65; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.113.197 (0.005 с.) |
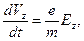 (19)
(19) - заряд, масса и скорость электронов пучка соответственно, Ez - усредненная по сечению пучка продольная составляющая электрического поля.
- заряд, масса и скорость электронов пучка соответственно, Ez - усредненная по сечению пучка продольная составляющая электрического поля. (20)
(20) и
и  -скорость и ускорение в координатах Лагранжа.
-скорость и ускорение в координатах Лагранжа.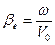 - постоянная распространения электронного пучка, V 0- средняя скорость пучка.
- постоянная распространения электронного пучка, V 0- средняя скорость пучка.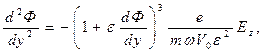 (22)
(22)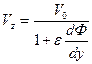 - скорость в фазовой системе координат.
- скорость в фазовой системе координат. (23)
(23)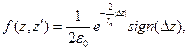 (24)
(24) , Dz=z-z’.
, Dz=z-z’. (25)
(25)


