
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основы вычислительной математикиСтр 1 из 11Следующая ⇒
Ю.П. Хрусталев
ОСНОВЫ ВЫЧИСЛИТЕЛЬНОЙ МАТЕМАТИКИ Практикум Для студентов, обучающихся по специальностям: : 2201 “Вычислительные машины, комплексы, системы и сети ” 2202 “Автоматизированные системы обработки информации и управления ” 719 «Информационные системы в технике и технологиях»
Издательство Иркутского государственного технического университета Рецензент – начальник отдела ИСЭМ СО РАН, д.т.н. профессор В.И. Зоркальцев Основы вычислительной математики. Практикум. Разработал доцент кафедры вычислительной техники Ю.П. Хрусталев – Иркутск, 2008 – с 94 Рассмотрены методы вычислительной математики. Проведен анализ погрешностей, возникающих при выполнений приближенных вычислений. Приведены алгоритмы решения основных задач вычислительной математики и показана методика их реализации с помощью системы MATHCAD. Для студентов, обучающихся по специальностям: : 2201 “Вычислительные машины, комплексы, системы и сети ” 2202 “Автоматизированные системы обработки информации и управления ” 719 «Информационные системы в технике и технологиях»
Библиография – Назв. – 7 Табл. – 6 http://detc.usu.ru/Assets/aMATH0021/l1_3.htm ОГЛАВЛЕНИЕ
1. Раздел 1. Погрешности вычислений Стр. 4 2. Раздел 2. Численные методы решения систем линейных алгебраических уравнений Стр. 14 3. Раздел 3. Решение нелинейных уравненийСтр. 40
4. Раздел 4. Интерполирование функций Стр. 46
5. Раздел 5. Численное интегрирование Стр. 65
6. Раздел 6. Численные методы решения обыкновенных дифференциальных уравнений Стр. 85 Раздел 1 Погрешности вычислений Краткое введение. Большинство величин, с которыми приходится встречаться в практике, являются приближенными, т.е. такими, точное значение которых неизвестно. Оценкой приближения такой величины к точному значению является погрешность, или ошибка. В практике используют абсолютные и относительные погрешности. Абсолютная погрешность ε - это разность между истинным и приближенным значением величины:
Относительная погрешность - это отношение величины абсолютной погрешности к приближению:
Для величин, близких по значению к единице, абсолютная и относительная погрешности имеют один порядок. Для очень больших и очень маленьких величин эти погрешности существенно отличаются. Например, если точное значение некоторой величины равно 0.00006, а приближенное значение 0.00005, то
Если с приближенными значениями проводить различные арифметические действия, то в результате получится приближенная величина, погрешность которой будет зависеть от погрешностей исходных величин и, как правило, будет больше этих величин. Погрешности будут вычисляться следующим образом:
СЛОЖЕНИЕ (ВЫЧИТАНИЕ)
УМНОЖЕНИЕ
ДЕЛЕНИЕ
Для уменьшения погрешности в практической деятельности рекомендуется соблюдать следующие правила: 1) По необходимости избегать вычитания двух почти равных чисел. 2) Использовать формулы типа a(b-c) = ab -ac; (b-c)/a = b/a - c/a.
Причины возникновения погрешностей 1) Неточное представление исходной информации. 2) Округление. 3) Ограничение бесконечного математического процесса конечным числом операций. Задача лабораторной работы - определение погрешностей третьего вида.
Лабораторная работа 1 Определение погрешностей при вычислении функций методом разложения их в степенной ряд Работа выполняется с использованием палитры программирования системы автоматизации математических вычислений Mathcad и системы Excel.
Задание на работу: вычислить значение функции по приближенной формуле с заданной точностью: 1) получить рекуррентное соотношение для вычисления последующего члена степенного ряда по предыдущему; 2) вычислить значение функции с помощью программы на Mathcadе; 3) вычислить значение функции, используя систему EXEL.
Варианты заданий
Требования к оформлению отчета Отчет по лабораторной работе должен содержать: - название работы - цель работы - математическую формулировку задачи (представление заданной функции степенным рядом, вывод рекуррентного соотношения и алгоритм решения) - тексты программы (в системе Mathcad и Excel) - результаты, полученные в процессе выполнения работы - выводы Вспомогательные материалы Пример вычисления функции f(x) = Sin(x) с заданной точностью eps = 0.000001 X = 0.5
1. Алгоритм решения задачи
1.1 В сумму, предварительно обнуленную, заносится первый член ряда. 1.2 Сумма сравнивается с точным значением функции. Если погрешность (модуль разности суммы и точного значения) не превосходит допустимого значения, задача считается решенной. В противном случае – переход к следующему шагу. 1.3 С помощью рекуррентной формулы вычисляется следующий член ряда и добавляется к сумме. 1.4 Переход на пункт 1.2. 2. Вывод рекуррентного соотношения (При выводе данного соотношения в общем члене ряда индекс i заменяется на i+1, полученный i+1 -й член делится на предыдущий)
3. Программа для вычисления синуса (При выполнении лабораторной работы разработка программы на языках высокого уровня не требуется! Программа приведена только для лучшего понимания алгоритма).
Program Lsb1; {**************************************************************** ПОГРЕШНОСТИ ВЫЧИСЛЕНИЙ ****************************************************************} Uses Crt; Var x,e,eps,a0,a1,r,s,y,z: real; i,n,k: integer; BEGIN ClrScr; WRITE(' Введите Х = '); READLN (x); WRITE (' Введите е = '); READLN (e); y:= Sin(x); WRITELN (' SIN (x) = ', y); WRITELN; a0:= x; i:= 0; eps:= y - a0; WRITELN (' N', ' S ', ' E'); WRITELN (' ', i+1, ' ', a0, ' ', eps); r:= - x*x; i:= 1; s:= a0; REPEAT n:= 2*i; z:= n*(n+1); a1:= r *a0/z; s:= s+a1; eps:= y-s; WRITELN (' ', i+1, ' ', s, ' ', eps); a0:= a1; i:= i+1; UNTIL abs (eps) < e; END. Результаты работы программы Введите X = 0.5 Введите е = 0.0000001 SIN (x) = 4.7942553860E-01
N S E
1 5.0000000000E-01 -2.0574461396E-02 2 4.7916666667E-01 2.5887193760E-04 3 4.7942708333E-0.1 -1.5447290025E -06 4 4.7942553323E-0.1 5.3701114666E- 09
4. Пример вычисления синуса в системе Excel
5. Решение задачи в системе Mathcad с использованием палитры программирования 5.1 Разработка программы в MathCAD Чтобы раскрыть палитру программирования, следует выполнить действия, показанные на рисунке 1.1
Рис. 1.1 Обращение к палитре программирования
Оператор Add Line обозначает в MathCAD программный модуль - вертикальную черту, справа от которой последовательно записываются операторы.
Оператор ç означает присваивание: F ç 2+B Создадим новый лист в MathCAD. Напишем оператор ORIGIN:= 1 – для того, чтобы MathCAD начинал нумерацию в массивах с 1, а не с нуля (по умолчанию нумерация начинается с нуля). Затем вводим исходные данные
Рис 1.2 Пример программы для вычисления функции y = Sin(x) Большая часть программы в комментариях не нуждается. Поясним только некоторые операторы. Оператор while содержит сложное условие выхода из цикла. Помимо проверки достижения заданной точности ограничено также число итераций (в приведенном примере число итераций не должно превышать пяти, хотя в общем случае оно должно быть много больше). Это ограничение позволяет избежать «зацикливания» программы, если она не верна, и процесс приближения функции степенным рядом не сходится. Текущие значения суммы и членов ряда запоминаются в одномерных массивах SS и B. Это необходимо для отладки программы. Кроме того, значения текущей суммы и членов степенного ряда позволяют наглядно представить процесс приближения функции. Программа возвращает переменную, расположенную в последней строке программы. Если необходимо в результате работы программы получить значения нескольких переменных, то их следует поместить в скобки, т. е. вывести вектор. Вектор задается с помощью палитры Math (изображение матрицы). При этом число строк должно равняться числу возвращаемых переменных. Матрица содержит один столбец. На рис.1.3 приведен пример вывода на экран результатов работы программы. В верхней части рисунка показан полный вектор возвращаемых переменных. Третья и четвертые строки сами являются векторами, на что указывает их изображение (фигурные скобки с указанием размерности выводимых матриц – 2,1, т. е. вектор, содержащий две строки). В данном примере число итераций равнялось двум. Ниже показан способ отображения этих векторов.
Рис. 1.3 Вывод на экран дисплея результатов работы программы
Контрольные вопросы 1.Назовите причины возникновения погрешностей. 2.Может ли относительная погрешность превышать абсолютную погрешность?
3.В каком случае относительная погрешность меньше абсолютной погрешности? 4.В каких единицах выражаются абсолютная и относительная погрешности?
Раздел 2 Варианты заданий. ( Система уравненийв матричной записи имеет вид Ax = b) 1. A=
3. A=
5. A= 7. A= 9. A=
11. A= 13. A=
15. A=
17. A=
19. A=
21. A=
Требования к оформлению отчета Отчет должен содержать: - Название и цель работы - Задание на работу - Текст программы на Mathcadе - Результаты работы программы - Проверку решения
Вспомогательные материалы Пример разработки программы для решения системы линейных агебраических уравнений в системе Mathcad Этап 1. Объявление переменных Определим переменные и зададим матрицу системы линейных уравнений:
Теперь определим матрицу А. Begin d1:=0; da:=0; lin:=False; For i:=0 to n-2 do For j:=i+1 to n-1 do Begin For k:=0 to n-1 do If matr[j,k]<>0 then d1:=d1+matr[i,k]/matr[j,k]; d1:=d1/n; For k:=0 to n-1 do If matr[j,k]<>0 then If d1=matr[i,k]/matr[j,k] then da:=da+1; If da=n then lin:=True; d1:=0; da:=0; end; If lin then Proverka:=True Else Proverka:=False;
Лабораторная работа 3 Раздел 3 Метод половинного деления Описание метода. Пусть дано уравнение f(x) = 0, (1) причем функция f(x) непрерывна на отрезке [ a, b] и f(a)f(b) < 0. Для вычисления корня уравнения (1), принадлежащего отрезку [ a, b], найдем середину этого отрезка x1 = (a + b) / 2. Если f(x1) Новый суженный промежуток [ a1, b1 ] снова делим пополам и продолжаем вычисления по разработанной схеме и т. д. В результате получаем либо точный корень уравнения (1) на каком - то этапе, либо последовательность вложенных отрезков [ a, b ], [ a1, b1 ], ..., [ a n, b n ],.. таких, что f(a n)f(b n) < 0 (n = 1, 2,...), (2) b n - a n = (1/ 2 n) (b- a) (3) Число ξ - общий предел последовательности { a n } и { b n } - является корнем уравнения f(x) = 0. Оценку погрешности решения на n -ом шаге вычислений можно получить из соотношения (3) в виде
0 < ξ - a n Здесь a n
 
       
Рис. 3.1 Наличие единственного корня уравнения на интервале [a,b]
Блок – схема алгоритма, реализующего метод половинного деления, приведена на рис. 3.3. Теорема.
1) 2) значения функции y = g(х) принадлежат отрезку [a,b] для любого x Тогда при любом выборе начального приближения x(0)
Оценка погрешности k -го приближения x (k) к корню
где Укажем теперь один из способов преобразования уравнения f(x) = 0 (9) к виду x = g(x), допускающему применение метода итераций, сходящихся к решению Для любого числа g (x) = x + Предположим, что производная f ' (x) > 0 и непрерывна на [ a,b ]. Пусть положим
и рассмотрим функцию
Для функции, определенной формулой (10), выполняются достаточные условия сходимости метода итераций решения уравнения (9). В частности, условие 1) теоремы следует из неравенств 0 < m 0 Замечание1. Если окажется, что производная f ' (x) отрицательна на отрезке [ a, b], то уравнение (1) можно заменить на равносильное уравнение -f(x) = 0 и использовать указанное преобразование. Замечание 2. Если вычисление точного числа Замечание 3. При нахождении корня уравнения (1) с заданной точностью или при оценке погрешности k-го приближения можно, не вычисляя точного значения числа q = max | g ' (x) |,ограничиться следующей практической рекомендацией:
Блок – схема алгоритма, реализующего итерационный метод, приведена на рис. 3.2.
                        
       
  
        
  
Рис 3.3 Блок – схема алгоритма, реализующего метод половинного деления
Лабораторная работа 4 Варианты заданий. 1. x 4 - 3x -20 = 0 (x > 0) 2. x 3 - 2x - 5 = 0 (x > 0) 3. x 3 + 3x + 5 = 0 4. x 4 + 5x -7 = 0 (x > 0) 5. x 3 - 12x - 5 = 0 (x > 0) 6. x 3 - 2x 2 - 4x + 5 = 0 (x < 0) 7. x + e x = 0 8. x 5 - x - 2 = 0 9. x 3 - 10x + 5 = 0 (x < 0) 10. 2 - lnx - x = 0 11. x 3 + 2x - 7 = 0 12. x 3 + x 2 - 11 = 0 (x > 0) 13..x 4 - 2x - 4 = 0 (x > 0) 14. 2e x + x - 1 = 0 15. x 4 - 2x - 4 = 0 (x < 0) 16. 2x 3 + x 2 - 4 = 0 (x > 0) 17. e x - x - 2 = 0 18. (1/2) e x - x - 1 = 0 (x > 0) 19. x 2 - cos x = 0 (x > 0) 20. x 2 + lnx = 0 Требования к оформлению отчета Отчет по лабораторной работе должен содержать: - название работы - цель работы - тексты программ - результаты, полученные в процессе выполнения работы - выводы Вспомогательные материалы Для разработки программ на Mathcad е можно использовать приемы, описанные в лабораторных работах №1 и №2. Существует бесчисленное множество линейных функций, имеющих корень на интервале[a,b]. Поясним это на примере. Пусть a = 2, b = 7. Пусть корень уравнения равен 5. Тогда функция F(x) = k1 + k2*x, имеющая корень, равный пяти, может иметь такой вид F(x) = 10 – 2*x (один из коэффициентов задается произвольно, другой находится из уравнения F(x) = 0).
Контрольные вопросы: 1. Зачем нужна процедура отделения корней? 2. Что называется корнем уравнения? 3. Какова точность метода половинного деления? 4. Каким образом исходное уравнение преобразуется к виду, удобному для итераций? 5. Чему равна оценка погрешности k -го приближения? Раздел 4 Интерполирование функций Краткое введение. Постановка задачи интерполирования. На отрезке
Требуется построить интерполирующую функцию F(x), принадлежащую известному классу и принимающую в узлах интерполяции те же значения, что и
Рис. 4.1 Интерполирование функции y = f(x)
В общем случае, задача имеет бесчисленное множество решений. Задача становится однозначной, если решение искать в заданном классе функций. Будем искать полином Полученную интерполяционную формулу Если При
Обратное интерполирование Задача обратного интерполирования: по заданному значению функции Предположим, что на отрезке [a, b], содержащем узлы интерполяции, функция f(x) монотонна. Тогда существует однозначная обратная функция x=F(y). Она задана той же таблицей, что и y=f(x), только теперь аргументом будет значение В этом случае обратное интерполирование сводится к обычному интерполированию для функции x=F(y). Т.е. строится интерполяционный многочлен (например, по формуле Лагранжа) – многочлен
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 336; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.132.194 (0.209 с.) |

 (1)
(1) (2)
(2)
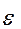 =
=  , а
, а  ( 20%). Если точное значение величины равно 100500, а приближенное 100000, то
( 20%). Если точное значение величины равно 100500, а приближенное 100000, то  , а
, а 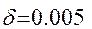 .
.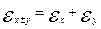
 (3)
(3)
 (4)
(4)
 (5)
(5) )
)


 (x)
(x)

 (x)
(x)
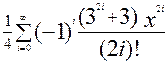











 =2Arcth(x)
=2Arcth(x)

 =2Arcth(x)
=2Arcth(x)


























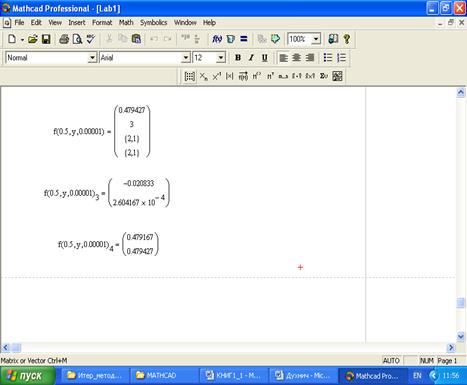
 , b=
, b=  2. A=
2. A=  , b=
, b= 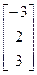
 , b=
, b= 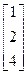 4. A=
4. A=  , b=
, b= 
 , b=
, b= 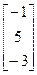 6. A=
6. A= 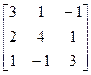 , b=
, b= 
 , b=
, b=  8. A=
8. A=  , b=
, b= 
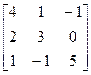 , b=
, b= 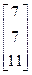 10. A=
10. A= 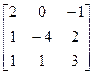 , b=
, b= 
 , b=
, b=  12. A=
12. A= 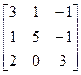 , b=
, b= 
 , b =
, b =  14. A=
14. A=  , b=
, b= 
 , b =
, b =  16. A=
16. A= 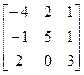 , b=
, b= 
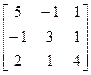 , b =
, b =  18. A=
18. A=  , b=
, b= 
 , b =
, b = 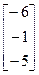 20. A=
20. A=  , b=
, b= 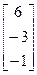
 , b =
, b = 
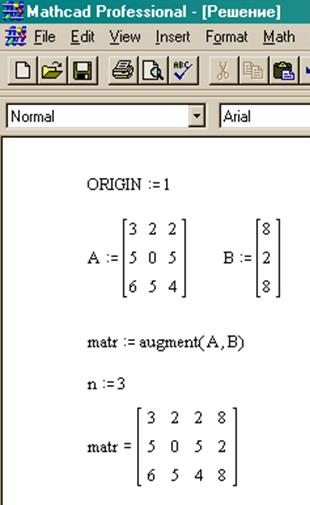 Создадим новый лист в MathCAD и для начала напишем оператор ORIGIN:= 1 – это для того чтобы MathCAD начинал нумерацию в матрицах с 1, а не с нуля.
Создадим новый лист в MathCAD и для начала напишем оператор ORIGIN:= 1 – это для того чтобы MathCAD начинал нумерацию в матрицах с 1, а не с нуля. end;
end;
 0, то для продолжения вычислений выберем ту из частей банного отрезка [ a, x1] или [ x1, b], на концах которой функция f(x) имеет противоположные знаки. Концы нового отрезка обозначим через a1 и b1 .
0, то для продолжения вычислений выберем ту из частей банного отрезка [ a, x1] или [ x1, b], на концах которой функция f(x) имеет противоположные знаки. Концы нового отрезка обозначим через a1 и b1 . (1/ 2 n) (b- a) = b n - a n (4)
(1/ 2 n) (b- a) = b n - a n (4) ξ c точностью ε не превышающей (1/ 2 n) (b- a).
ξ c точностью ε не превышающей (1/ 2 n) (b- a).




 Пусть функция g (x) имеет на отрезке [a, b] непрерывную производную и выполнены два условия:
Пусть функция g (x) имеет на отрезке [a, b] непрерывную производную и выполнены два условия: q < 1 при x
q < 1 при x  [a, b];
[a, b]; уравнения (1) на отрезке [a, b]
уравнения (1) на отрезке [a, b] , (8)
, (8)
 уравнение (9) равносильно уравнению (5), где
уравнение (9) равносильно уравнению (5), где f(x).
f(x).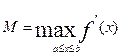 ,
,  ;
;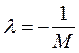 ,
, 
 . (10)
. (10) .
. затруднительно, то можно заменить его произвольным числом М1> M. Однако при большом М1 число q = 1 - m / М1 ближе к единице и процесс итераций сходится медленнее.
затруднительно, то можно заменить его произвольным числом М1> M. Однако при большом М1 число q = 1 - m / М1 ближе к единице и процесс итераций сходится медленнее. при 0 < q
при 0 < q  при (1/2) < q < 1. (12)
при (1/2) < q < 1. (12)






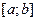 заданы n+1 точки
заданы n+1 точки  , которые называются узлами интерполяции, и значение некоторой функции
, которые называются узлами интерполяции, и значение некоторой функции  в этих точках
в этих точках . (1)
. (1)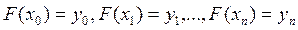 (2)
(2)
 степени не выше n и удовлетворяющий условию (2).
степени не выше n и удовлетворяющий условию (2). используют для вычисления значений
используют для вычисления значений  - имеет место задача интерполирования (интерполирование “в узком смысле”).
- имеет место задача интерполирования (интерполирование “в узком смысле”).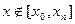 решается задача экстраполирования.
решается задача экстраполирования. найти аргумент
найти аргумент 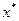 , при котором
, при котором  . Функция y=f(x) задана таблично.
. Функция y=f(x) задана таблично. , а
, а 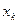 -соответствующее значение функции.
-соответствующее значение функции. . При подстановке в
. При подстановке в  .
.


