
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Пакет PDE Tools системи MATLAB для розв’язання крайових задач із частинними похіднимиСтр 1 из 8Следующая ⇒
Чисельні методи Частина 4 Методичні вказівки до лабораторних робіт
Для студентів всіх форм навчання спеціальності 6.040303 - Системний аналіз
Чисельні методи. Частина 4. Методичні вказівки до лабораторних робіт. Для студентів денної форми навчання спеціальності 6.040303 – Системний аналіз. / Укл.: Біла Н.І., Денисенко О.І., Подковаліхіна О.О. - Запоріжжя: ЗНТУ, 2013. – 90 с.
Містить теоретичні відомості, приклади, задачі для самостійного розв'язання, завдання до лабораторних робот з курсу “Чисельні методи ” за темою "Чисельні методи розв’язання задач математичної фізики".
Укладачі: Біла Н. І. доцент, Денисенко О.І., доцент, Подковаліхіна О.О., доцент.
Рецензенти: Пінчук В. П., доцент Вишневська В.Г., доцент.
Відповідальний за випуск Корніч Г. В., зав. кафедрою, професор
Затверджено на засіданні кафедри Системного аналізу та обчислювальної математики, протокол № 6 від 28.12.2012
Зміст Пакет PDE Tools системи MATLAB для розв’язання крайових задач із частинними похідними 1.1 Рівняння математичної фізики...........................4 1.2 Виконання розрахунків в пакеті MATLAB.........................8 1.3 Задачі для самостійного розв’язання...........................21 1.4 Завдання до лабораторної роботи...........................22 1.5 Контрольні питання...........................24 Метод сіток розв'язання еліптичниз рівнянь 2.1Метод сіток – постановка задачі..........................25 2.2 Побудова сітки й апроксимація рівняння...........................25 2.3 Вирішення системи алгебраїчних рівнянь.........................28 2.4 Погрішність вирішення й збіжність..........................32 2.5 Задача для самостійного вирішення на практиці..............34 2.6 Завдання до лабораторної роботи..........................34 2.7 Контрольні питання...........................35 Метод сіток розв'язку крайових задач для рівнянь параболічного типу 3.1 Постановка задачі......................................36 3.2 Явна різницева схема......................................38 3.3 Неявна різницева схема......................................43 3.4 Різницеві схеми підвищеної точності. Схема Кранка-Нікольсона.......................................44 3.5 Задачі для самостійного розв'язку на практиці........................47 3.6 Завдання до лабораторної роботи.......................................48 3.7 Контрольні питання.......................................50
Метод сіток розв'язку крайових задач для хвильових рівнянь 4.1 Постановка задачі......................................51 4.2 Явна схема.......................................52 4.3 Неявна схема.......................................59 4.4 Задача для самостійного розв'язку на практиці.......................62 4.5 Завдання до лабораторної роботи.......................................63 4.6 Контрольні питання.......................................65 Методи розв'язку інтегральних рівнянь 5.1 Загальні відомості про інтегральні рівняння 5.2 Метод послідовних наближень розв'язку інтегральних рівнянь Фредгольма 5.3 Квадратурний метод розв'язку інтегральних рівнянь Фредгольма 5.4 Загальні відомості про інтегральні рівняння Вольтерра 5.5 Метод послідовних наближень розв'язку інтегральних рівнянь Вольтерра 5.6 Квадратурний метод розв'язку інтегральних рівнянь Вольтерра 5.7 Завдання до лабораторної роботи 5.8 Контрольні питання Методи апроксимуючих функцій розв'язку інтегральних рівнянь Загальний підхід 8.2 Метод колокацій 8.3 Метод найменших квадратів Метод Гальоркіна 8.5 Завдання до лабораторної роботи 8.6 Контрольні питання
Література Пакет PDE Tools системи Matlab для розв’язання крайових задач із частинними похідними Рівняння параболічного типу. Прикладом рівняння параболічного типу є
Одним із варіантів використання рівняння (1.2) є моделювання процесів теплопровідності чи дифузії, де Для рівняння теплопровідності за граничних умов
і початкової умови
маємо першу мішану крайову задачу. Функції Рівняння теплопровідності за граничних умов
і початкової умови (1.4) визначають другу мішану крайову задачу. У цьому випадку на границях задані теплові потоки. Рівняння теплопровідності за граничних умов
і початкової умови (1.4) визначають третю мішану крайову задачу. Граничні умови задають теплообмін між газоподібним або рідким середовищем з відомими температурами
Рівняння еліптичного типу. Прикладом рівнянь еліптичного типу є рівняння Лапласа:
чи рівняння Пуассона:
Одним із прикладів використання рівняння (1.9) або (1.10) є моделювання потоку ідеальної рідини в стаціонарних потоках, стаціонарного розподілу температури або напруженості електричних чи магнітних полів. Рівняння Лапласа описує ці процеси у разі відсутності джерел енергії чи стоків, а рівняння Пуассона – ті ж самі процеси за наявності розподілених в області Оскільки рівняння Лапласа і Пуассона – стаціонарні, то в постановці задачі задаються тільки граничні умови. Залежно від граничних умов маємо: – першу крайову задачу для рівняння Лапласа (задача Діріхле):
– другу крайову задачу для рівняння Лапласа (задача Неймана):
– третю крайову задачу для рівняння Лапласа:
При цьому в другій і третій крайових задачах похідні слід обчислювати у напрямку зовнішньої нормалі Розв’язок Математична постановка задачі Рівняння:
Граничні умови:
Координати центрів: Запуск додатку PDE Toolbox Запуск додатку призводить до появи на екрані вікна графічного інтерфейсу. Для цього в командному рядку набираємо: >> pdetool У верхній частині інтерфейсу рис. 1.2 розташовується рядок головного меню, що включає пункти "File", "Edit" та інші. Безпосередньо під головним меню розміщена панель, що включає інструменти PDETool, список видів завдань "Application" і покажчик значень координат x і y. Нижче розташовані вікно "Set formula" (введення формули) і власне графічне вікно для роботи з зображенням розрахункової області. Внизу є інформаційний рядок "Info" і кнопка "Exit" (вихід).
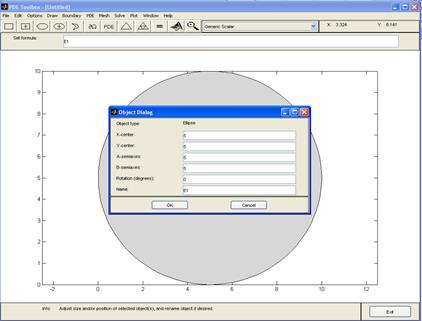
Рисунок 1.2 – Область задачі Перший етап розв’язку На першому етапі необхідносформувати вхідну геометрію задачі в графічному вікні інтерфейсу PDETool. Зображення формуються за допомогою команд пункту Draw (Рисувати) головного меню: Draw Mode – перемикання в режим введення (прорисовки) геометрії; Rectangle/square – створення прямокутника або квадрата за допомогою миші починаючи від його верхньої лівої вершини; Rectangle/square (centered) – створення прямокутника або квадрата за допомогою миші починаючи від його центру; Ellipse/circle – створення еліпса або кола за допомогою миші починаючи від верхньої лівої точки; Ellipse/circle (centered) – створення еліпса або кола за допомогою миші починаючи від центру; Polygon – прорисовка багатокутника відрізками ламаної лінії, поки вона не стане замкнутою; Rotate – поворот виділених об'єктів навколо деякої точки; Export Geometry Description, Set Formula, Labels… – експорт в базову робочу область MATLAB змінних опису геометрії. Для того, щоб нарисувати коло чи квадрат, необхідно натиснути клавішу Shift і вибрати відповідну фігуру. Для того, щоб встановити розмірності області даної задачі, потрібно в меню Option вибрати Axes Limits… У рядку X-axis range набрати [0 10], у рядку Y-axis range набрати [0 10] (рис. 1.2). За допомогою панелі інструментів потрібно нарисувати канал. Спочатку рисуємо коло з центром в точці (0,0) і радіусом 5. Для уточнення координат двічі клацаємо по колу. У вікні Object Dialog встановлюємо параметри (рис. 1.3):
X-center 5 Y-center 5 A-semiaxes 5 B-semiaxes 5. Щоб вирівняти осі в меню Option обираємо Axes Equal. Аналогічно рисуємо друге коло з центром в точці (7,3) і радіусом 1, і прямокутник довжини 10 і ширини 1. У рядку Set formula набираємо: E1-E2-R1 (рис. 1.4).
Рисунок 1.3 – Параметри об’єкту Команди для редагування зображення і настройки графічного вікна містяться в наступних пунктах головного меню. Edit (Правка) містить команди: Undo – скасування останньої дії; Cut – вирізати виділений геометричний об'єкт і помістити його в буфер; Copy – копіювати виділений об'єкт в буфер; Paste – вставити геометричний об'єкт з буфера; Clear – видалити виділений об'єкт; Select All – виділити все геометричні об'єкти. Options (Опції) містить команди: Grid – показати/сховати координатну сітку; Grid Spacing – встановити межі і крок сітки; Snap – округляти координати покажчика миші; Axes Limits – встановити межі координатних осей; Axes Equal – встановити однаковий масштаб по осях x і y; Zoom – показати зі збільшенням виділену частину моделі; Application – перемикання виду задачі; Refresh – оновити зображення моделі.
Рисунок 1.4 – Призматичний канал Другий етап розв’язку Другий етапвключає введення граничних умов на граничних сегментах і параметрів рівняння. Визначити умови на кожному із сегментів можна, виділивши його подвійним клацанням лівої кнопки миші. Відповідні команди розташовуються в розділах Boundary і PDE головного меню. Boundary (Межі) містить команди: Boundary Mode – введення граничних умов; Specify Boundary Conditions… – введення параметрів граничних умов; Show Edge Labels – показати номера граничних сегментів; Show Subdomain Labels – показати номери зон; Remove Subdomain Border – видалити границю зон; Remove All Subdomain Borders – видалення всіх границь зон; Export Decomposed Geometry, Boundary Cond’s… – експорт в робочу область MATLAB змінних опису граничних умов. PDE (Рівняння) містить команди: PDE Mode – перемикання в режим введення параметрів рівняння; Show Subdomain Labels – показати номери зон; PDE Specification… – введення параметрів (коефіцієнтів) рівняння; Export PDE Coefficients… – експорт в базову робочу область змінних, що описують PDE коефіцієнти в розрахунковій області. В меню Boundary оберемо Boundary Mode. Два рази клацаємо по межі
Задамо параметри рівняння еліптичного типу, викликавши через меню або панель інструментів вікно "PDE Specification". Оберемо тип рівняння – "Elliptic". Задамо
Рисунок 1.5 – Граничні умови Якщо в списку "Application" установлено режим "Electrostatics" (задача електростатична), то у вікні MATLAB рівняння має вигляд
де діелектрична – діелектрична проникність, У тому випадку, коли встановлено режим "Generic Scalar" у списку "Application" (задача в узагальненій скалярній формі), запис рівняння в MATLAB має вигляд
Рисунок 1.6 – Параметри рівняння Третій етап розв’язку На третьому етапі формується сітка скінченних елементів(рис. 1.7). PDE Toolbox підтримує тільки симплекс-елементи, для яких характерні лінійні функції форми. Пункт Mesh (Сітка) головного меню містить наступні команди: Undo Mesh Change – скасувати останню зміну сітки; Display Triangle Quality – відобразити в кольорі показник регулярності кінцевих елементів; Show Node Labels – показати номери вузлів; Show Triangle Labels – показати номери кінцевих елементів; Parameters… – встановити параметри генератора сітки; Export Mesh – експорт сітки в базову робочу область. Четвертий етап розв’язку Четвертий етап містить власне розв’язок задачі та його вивід у графічному вигляді(рис. 1.8). Відповідні команди розташовуються в пунктах Solve та Plot головного меню. Solve (Розв’язок) містить команди: Solve PDE – розв’язати крайову задачу; Parameters … – встановити параметри вирішувача; Export Solution… – експорт рішення в базову робочу область. Для отримання ізоліній в меню Plot обираємо Parameters …, де обираємо Contour. Результати розрахунку можна зберегти, звернувшись до пункту File (Файл) меню, що включає команди: New – створити нову модель; Open… – відкрити раніше збережену в m-файлі модель; Save – збереження моделі в m-файлі з поточним ім’ям; Save As… – збереження моделі в m-файлі; Print… – друк рисунка.
Рисунок 1.7 – Формування сітки
Рисунок 1.8 – Розподіл еквіпотенціальних ліній
Приклад 1.2. Розглянемо задачу теплопровідності для прямокутної пластини, поверхня якої теплоізольована, на границях пластини підтримується постійна температура, а на поверхні пластини встановлені джерела тепла, які також мають постійну температуру на границях контакту з пластиною. Пластина має початкову температуру Розв’язок Математична модель задачі буде мати наступний вигляд. Рівняння теплопровідності:
Граничні умови першого роду:
Початкова умова:
Рисунок 1.9 – Прямокутна пластина
Розрахунок проведемо в безрозмірному вигляді для таких значень параметрів:
Геометричні параметри пластини виберемо такими:
На рис. 1.10 наведено розв’язок задачі для значення
Рисунок 1.10 – Розв’язок задачі із прикладу 1.2
Приклад 1.3. Розглянемо задачу коливань тонкої мембрани. Мембраною називають тонку плівку, яка рівномірно натягнута на контур Г. Нехай в положенні рівноваги мембрана знаходиться в площині xOy та займає деяку область D(x,y). Відомо, що коливання мембрани описується двовимірним диференціальним рівнянням гіперболічного типу
де
які відображають початкове відхилення та початкову швидкість точок мембрани. Гранична умова В якості прикладу розглянемо коливання тонкої мембрани, яка має форму прямокутника.
Рисунок 1.11 – Прямокутна мембрана
Сформулюємо задачу в безрозмірному вигляді наступним чином:
На рис. 1.12 наведено розв’язок задачі для значення
Рисунок 1.12 – Розв’язок задачі із прикладу 1.3
Розв'язок. Оберемо кроки сітки по
Побудуємо різницеву схему:
з урахуванням рівності кроків по
Рисунок 2.3 – Сітка для прикладу 2.1. Із граничних умов маємо:
Запишемо отриману систему – (2.4).
1. Задамо величинам 2. Перерахуємо значення у внутрішніх точках, тобто одержимо перше наближення розв'язку системи за методом Зейделя:
3. Підрахуємо друге наближення:
Запишемо матрицю
Повторюємо ітерації доти, поки значення у вузлах сітки будуть відрізнятися на двох сусідніх ітераціях більше, ніж бажана точність розв'язку системи
що можна вважати наближеним розв'язком задачі. Таблиця 2.2 – Варіанти індивідуальних завдань
2.7. Контрольні питання 1. Які види сіток використовуються в методі кінцевих різниць? Яким чином будують на цих сітках різницеві апроксимації рівнянь і відповідні їм шаблони? 2. Які прямі й ітераційні методи використовують для розв'язку систем алгебраїчних рівнянь у задачах з диференційними рівняннями із частинними похідними (ДРЧП)? 3. Дайте характеристику ітераційних методів, що використовуються для розв'язку систем алгебраїчних рівнянь у задачах з ДРЧП. 4. Як задаються граничні умови? Яким чином задається початкове наближення при вирішенні ДРЧП із використанням ітераційних методів? Відповідь поясніть на прикладі. 5. З яких міркувань вибирають крок сітки в методі кінцевих різниць? МЕТОД СІТОК Постановка задачі Розглянемо розв'язок змішаної крайової задачі для диференційних рівнянь з частинними похідними (ДРЧП):
с початковою умовою:
і граничними умовами:
Розглянуте рівняння описує розподіл температури в стрижні, початкова температура якого дорівнює значенню функції Для розв'язку задачі методом кінцевих різниць побудуємо прямокутну сітку (рис. 3.1), вузли якої визначаються формулами:
Значення Замінимо частинні похідні в рівнянні теплопровідності їх кінцево-різницевими апроксимаціями в кожному внутрішньому вузлі:
Вираз (3.2) можна вважати наближенням похідної як у точці Вираз (3.3) апроксимує похідну з порядком Для розв'язку змішаної крайової задачі необхідно апроксимувати похідну в граничній умові на правому кінці:
Використовуючи кінцево-різницеву апроксимацію, одержуємо:
Порядок апроксимації останньої формули Явна різницева схема Підставимо вирази (3.2) і (3.3) у рівняння (3.1) і розв'яжемо його щодо значень функції на верхньому часовому шарі:
Формула (3.5) вирішує поставлену задачу, оскільки вона виражає розв'язок у момент часу i+1 через розв'язок у момент часу i. З (3.4) знаходимо: Алгоритм обчислень за явною схемою реалізується наступною послідовністю дій. 1. Обчислюємо значення сіткової функції на першому часовому шарі з початкових умов: 2. Знаходимо розв'язок на сітковому шарі
3. Обчислюємо величину Завершивши кроки 1-3 одержуємо розв'язок при Недолік явної схеми: якщо крок за часом яка накладає досить жорсткі обмеження на крок за часом ( Приклад 3.1. Обчислити за допомогою явної схеми наближений розв'язок змішаної задачі
с початковою умовою Розв'язок. Формула (3.5) з урахуванням кроків по
Схема стійка, якщо
Рисунок 3.2 – Просторово - часова сітка для прикладу 3.1 З початкових умов одержимо:
із граничних умов одержимо
Підрахуємо значення для
Аналогічно обчислюємо для інших значень u=1.0000 0.6000 0.2000 0.2000 0.6000 1.0000 1.0000 0.6000 0.4000 0.4000 0.6000 1.0000 1.0000 0.7000 0.5000 0.5000 0.7000 1.0000 1.0000 0.7500 0.6000 0.6000 0.7500 1.0000 1.0000 0.8000 0.6750 0.6750 0.8000 1.0000 1.0000 0.8375 0.7375 0.7375 0.8375 1.0000 Графіки розв'язку для всіх моментів часу наведені на рис. 3.3. Початковий розподіл температури позначений на графіку неперервною лінією. Щоб отримати оцінку погрішности рішення, проведемо розрахунки з кроком по координаті в два рази менше, тобто Програма, що виконує розрахунки:
% приклад 5.1 n=11;hx=0.1; m=2*(n-1)+1; ht=0.005; u=zeros(m,n); a=1; sig=a^2*ht/hx^2; x=0:hx:1; u(1,:)=abs(2*x-1); t=0:ht:1; v=abs(2*t-1); plot(t,v, 'LineWidth',2); hold on; grid on for i=1:m-1 u(i+1,1)=1; u(i+1,n)=1; for j=2:n-1 u(i+1,j)=u(i,j)+sig*(u(i,j-1)- end end plot(x,u(5,:),'--o','LineWidth',2) plot(x,u(9,:),':s','LineWidth',2) plot(x,u(13,:),'-.*','LineWidth',2) plot(x,u(17,:),'--<','LineWidth',2) plot(x,u(21,:),'-->','LineWidth',2)
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 603; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.183.172 (0.44 с.) |
 . (1.2)
. (1.2) – коефіцієнт теплопровідності (якщо
– коефіцієнт теплопровідності (якщо  – температура) або масо-перенесення (якщо
– температура) або масо-перенесення (якщо  ), так і граничні умови (для
), так і граничні умови (для  ).
). ,
,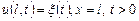 (1.3)
(1.3) (1.4)
(1.4) задають температуру на границях
задають температуру на границях  .
. ,
, (1.5)
(1.5) ,
, (1.6)
(1.6) на границі
на границі  та
та  на границі
на границі  з невідомими температурами
з невідомими температурами  . Коефіцієнти
. Коефіцієнти  – відомі коефіцієнти теплообміну між газоподібним або рідким середовищем і відповідною границею.
– відомі коефіцієнти теплообміну між газоподібним або рідким середовищем і відповідною границею. , (1.9)
, (1.9) . (1.10)
. (1.10) джерел, що задаються правою частиною рівняння –
джерел, що задаються правою частиною рівняння – 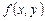 .
.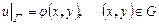 (1.11)
(1.11) (1.12)
(1.12) . (1.13)
. (1.13) відносно області
відносно області  ,
, ,
, ,
,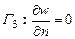 .
. ,
, 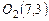 .
.

 , у вікні обираємо Dirihlet,
, у вікні обираємо Dirihlet,  (т.к.
(т.к.  ). Для даної задачі межа
). Для даної задачі межа  . На межі
. На межі  обираємо Neumann,
обираємо Neumann,  .
.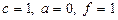 (рис. 1.6).
(рис. 1.6).

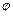 – електричний потенціал,
– електричний потенціал, 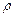 – об’ємний заряд.
– об’ємний заряд. .
.


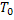 . Геометрія пластини зображена на рис. 1.9.
. Геометрія пластини зображена на рис. 1.9.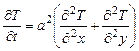 .
. .
. .
.
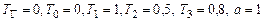 .
. (значення часу
(значення часу  та початкової температури
та початкової температури  потрібно задавати командами Solve/Parameters…).
потрібно задавати командами Solve/Parameters…).
 ,
, ,
,  – натяг мембрани,
– натяг мембрани,  – відхилення мембрани від положення рівноваги. Постановка задачі передбачає початкові умови
– відхилення мембрани від положення рівноваги. Постановка задачі передбачає початкові умови ,
,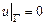 відображає закріплення мембрани по контуру
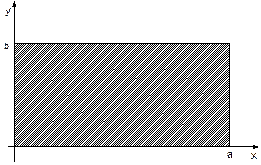
відображає закріплення мембрани по контуру  .
.
 ,
,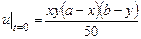 ,
,  .
. потрібно задавати командами Solve/Parameters…).
потрібно задавати командами Solve/Parameters…).
 та по
та по  рівними:
рівними:  . В цьому випадку маємо 6 внутрішніх вузлів, в яких треба обчислити температуру (рис. 2.3). Назвемо сіткову функцію
. В цьому випадку маємо 6 внутрішніх вузлів, в яких треба обчислити температуру (рис. 2.3). Назвемо сіткову функцію  .
. Рисунок 2.2 – Пластина прикладу 2.1.
Рисунок 2.2 – Пластина прикладу 2.1.
 ,мм
,мм
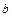 ,мм
,мм
 , °З
, °З
 , °З
, °З

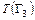 , °З
, °З
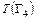 , °З
, °З
 ,
, ) маємо:
) маємо: .
.
 ,
,  ,
,  ,
, 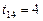 ,
, 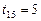 ;
; ,
,  ;
;  ,
,  ;
;  ,
,  ,
,  ,
,  ,
, 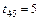 .
.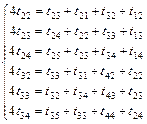 (2.6)
(2.6) .
. ;
; ;
; ;
; ;
; ;
;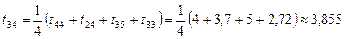 .
.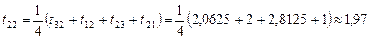 ;
; ;
; ;
;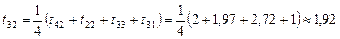 ;
; ;
; .
. другого наближення:
другого наближення: .
.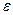 . Нехай
. Нехай  , тоді на шостій ітерації можна вважати, що задана точність розв'язку системи досягнута. Після шостої ітерації матриця розв'язку дорівнює
, тоді на шостій ітерації можна вважати, що задана точність розв'язку системи досягнута. Після шостої ітерації матриця розв'язку дорівнює
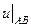



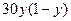
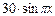























 ,
,  ,
,  (3.1)
(3.1) ,
, 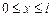
 ,
,  ,
, 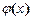 . Температура на лівому кінці стрижня змінюється за законом
. Температура на лівому кінці стрижня змінюється за законом  , на правому кінці стрижня відбувається теплообмін з навколишнім середовищем, температура якого визначається функцією
, на правому кінці стрижня відбувається теплообмін з навколишнім середовищем, температура якого визначається функцією  .
. ,
,  ,
,  ,
,  .
. на лівій і нижній границях сітки відомі з початкових і граничних умов. На правій границі відоме значення частинної похідної розв'язку рівняння по змінній
на лівій і нижній границях сітки відомі з початкових і граничних умов. На правій границі відоме значення частинної похідної розв'язку рівняння по змінній  .
. , (3.2)
, (3.2) (3.3)
(3.3)
 так і в точці
так і в точці  порядку
порядку  .
.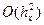 . Таким чином, порядок апроксимації диференційного рівняння
. Таким чином, порядок апроксимації диференційного рівняння 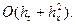
 .
. (3.4).
(3.4). .
. . (3.5)
. (3.5) . (3.6)
. (3.6) .
.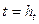 , використовуючи явну формулу:
, використовуючи явну формулу: ,
,  ,
,  .
. за формулою (3.6)
за формулою (3.6)  .
. повторюють кроки 2,3, збільшивши
повторюють кроки 2,3, збільшивши  на одиницю й використовуючи
на одиницю й використовуючи  виявляється досить великим у порівнянні із кроком по
виявляється досить великим у порівнянні із кроком по  ,
, ) і веде до значного збільшення часу для отримання рішення. Така схема називається умовно стійкою.
) і веде до значного збільшення часу для отримання рішення. Така схема називається умовно стійкою. ,
,  ,
,  ,
,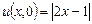 й граничними умовами
й граничними умовами  .
. і по
і по  після перетворень прийме вигляд:
після перетворень прийме вигляд: .
. . Перевіримо:
. Перевіримо: 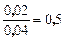 , тобто обрана різницева схема є стійкою.
, тобто обрана різницева схема є стійкою.
 ,
, 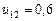 ,
,  ,
,  ,
,  ,
,  ;
; ,
,  ;
;  ,
,  ;
; 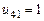 ,
,  .
. :
: ;
;


 , та з кроком за часом в чотири рази менше, тобто
, та з кроком за часом в чотири рази менше, тобто  . (Рішення з кроком за часом
. (Рішення з кроком за часом  виявилось нестійким, дуже швидко зростала погрішність!)
виявилось нестійким, дуже швидко зростала погрішність!)


