
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Граф цепи. Топологические матрицы
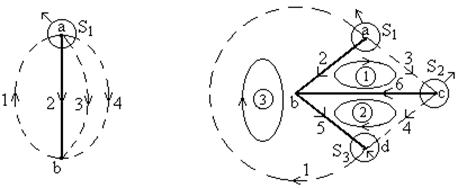
Из (1.2), (1.6) и (1.7) следует, что взаимосвязи между напряжениями (токами) отдельных элементов (ветвей) определяются не характером элементов, а способом их соединения или, как говорят, их топологией (геометрией). Для составления указанного вида уравнений, отображающих структуру цепи, достаточно изобразить упрощенную схему цепи в виде ее узлов и ветвей – простых линий, соединяющих эти узлы без указания элементов. Такое изображение называют г р а ф о м. На рис. 1.8, а и б представлены графы цепей, соответствующие схемам рис. 1.7, а и б. Форма линий при этом никакого значения не имеет.
а б Рис. 1.8 Если на ветвях графа изображены стрелки, указывающие направления токов ветвей, граф называют направленным. В противном случае граф – ненаправленный. При описании графов цепей используются те же понятия: узел, ветвь, контур, а также: дерево графа, хорда, сечение. При этом в теории графов ветвью часто считается каждый отдельно взятый элемент, так что узел – место соединения двух и более ветвей. Положительным направлением ветвей считается направление от узла. Д е р е в о г р а ф а – часть графа, включающая все узлы графа, не имеющая ни одного контура. На рис. 1.8, а дерево образовано одной ветвью, а на рис. 1.8, б – тремя, показанными сплошными линиями. Очевидно, что дерево графа содержит q – 1 ветвь, где q – число узлов. При этом любой граф содержит несколько деревьев. Х о р д ы или в е т в и с в я з и – ветви, не вошедшие в выбранное дерево. На рис. 1.8 – это пунктирные линии. С е ч е н и е г р а ф а – набор ветвей, удаление которых делит граф (схему) на две изолированные части (подграфы). Для анализа цепей значение имеют не все сечения и не все контуры, а только главные. Г л а в н о е с е ч е н и е – сечение, состоящее из ветвей связи и только одной ветви дерева. На рис. 1.8 главное сечение показано замкнутыми линиями со стрелками, указывающими положительное направление сечения, совпадающее с направлением ветви дерева. Число главных сечений равно число ветвей дерева, т. е. (q – 1). Г л а в н ы м называют контур, состоящий из ветвей дерева и только одной ветви связи (хорды). Направление контура определяется направлением входящей в него хорды. Число главных контуров равно числу хорд, причем сумма главных контуров и главных сечений равна числу ветвей графа. На рис. 1.8, б главные контуры обозначены цифрами 1, 2, 3.
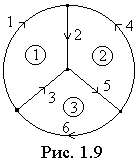
Топологические свойства графа (его структура) могут быть записаны аналитически с помощью матриц: узловой (А), контурной (В) и сечений (Q). Узловая матрица (иногда ее называют матрицей соединений) описывает соединение ветвей по отношению к узлам, контурная – по отношению к главным контурам, а сечений – по отношению к главным сечениям. Матрицы представляют собой таблицы с числом столбцов, равным числу ветвей, и числом строк, равным числу узлов без единицы, числу главных контуров и числу главных сечений соответственно для узловой, контурной и сечений. Коэффициенты матрицы равны +1, если ветвь принадлежит данному узлу, контуру или сечению, причем направление ветви совпадает с положительным направлением по отношению к узлу, контуру и сечению. В противном случае коэффициент матрицы равен –1. Если ветвь не принадлежит узлу, контуру или сечению, коэффициенты матриц – нулевые. Для графа по рис. 1.8, б узловая матрица:
Узел, для которого строка матрицы не заполняется, называют базисным. Его выбирают произвольно. В данном примере за базисный узел принят узел d. Матрицы контуров и сечений для этого же графа, имеют вид:
РЕШЕНИЕ. Обратим внимание, что ветвь 2 является общей для контуров 1 и 2; ветвь 3 – для контуров 1 и 3; ветвь 5 – для контуров 2 и 3. Изобразив эти ветви, как показано на рис. 1.9, и дополнив образованное дерево (подграф) ветвями связи согласно заданной матрице, получаем соответствующий граф.
ЗАДАЧИ ИССЛЕДОВАНИЯ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ. ОБЩИЕ ВОПРОСЫ ФОРМИРОВАНИЯ УРАВНЕНИЙ
Исследование электрических цепей может преследовать различные цели. Наиболее часто требуется произвести полный расчет токов и напряжений цепи известной структуры по заданным воздействиям (источникам). В этом случае говорят о з а д а ч е а н а л и з а э л е к т р и ч е с к о й ц е п и. Анализ может быть частичным, если требуется рассчитать выходную величину – реакцию цепи на действие входного воздействия. Такую задачу называют анализом по входу и выходу.
Иногда исследование цепи выполняют для определения ее параметров. Их находят по результатам измерения токов и напряжений на отдельных участках цепи. Такое исследование – задача диагностики. Если исследование имеет цель определить структуру и параметры элементов цепи, обеспечивающих необходимое преобразование входной величины, говорят о з а д а ч е с и н т е з а. Задачи синтеза – основа конструирования любого электротехнического устройства. Это наиболее сложный раздел теории электрических цепей. Ниже рассматриваются вопросы, связанные с анализом цепей. Анализ цепи, как следует из вышесказанного, заключается в отыскании токов и напряжений ветвей, число которых (n) определяет число неизвестных: n неизвестных токов и n неизвестных напряжений (2n). Первый этап анализа – составление системы независимых уравнений, позволяющих определить все неизвестные или отдельные из них согласно требованиям конкретной задачи. Система формируется из уравнений двух типов: 1) уравнений, описывающих характеристики ветвей – зависимости между напряжениями и токами; 2) уравнений, отображающих информацию о структуре (соединениях) цепи. Уравнения характеристик ветвей (как и отдельных элементов) называют к о м п о н е н т н ы м и. Компонентными уравнениями являются: закон Ома, взаимосвязи между напряжением и током индуктивного и емкостного элементов (табл. 1.1), токов и ЭДС зависимых источников с величиной управления (табл. 1.2). Компонентные уравнения ветвей, состоящих из группы элементов, например, представленных на рис. 1.6, а и 1.6, б, получают суммированием напряжений и токов отдельных элементов. Для ветвей по рис. 1.5 компонентными будут уравнения (1.5). Компонентные уравнения не связаны между собой, они относятся только к одной определенной ветви. Уравнения второго типа называют структурными уравнениями или уравнениями соединений. Они составляются по законам Кирхгофа (1.2), которые определяют равновесие токов (первый закон) и равновесие напряжений (второй закон) цепи. Первый закон применим к узлам и сечениям электрических схем. Его формулировка: для любой электрической цепи (с сосредоточенными параметрами), для любого из ее узлов (сечений) и для любого момента времени алгебраическая сумма токов всех ветвей, присоединенных к узлу (входящих в сечение), равна нулю. Второй закон применим к контурам. Он гласит: для любой цепи (с сосредоточенными параметрами), для любого из ее контуров, для любого момента времени алгебраическая сумма напряжений ветвей, образующих контур, равна нулю. Входящие в уравнения (1.2) величины суммируются алгебраически. Положительными считаются величины, совпадающие с положительными направлениями для узла, сечения или контура. Иногда второй закон Кирхгофа записывают в форме:
где напряжения источников ЭДС заменены значениями ЭДС этих источников. При такой записи со знаком ²плюс² учитываются ЭДС источников, направление действия которых совпадает с направлением обхода контура. Чтобы система структурных уравнений не была избыточной, по первому закону Кирхгофа составляются уравнения только для главных сечений или для всех узлов, кроме одного (базисного).
По второму закону Кирхгофа уравнения записывают т о л ь к о для главных контуров.
ПРИМЕР 1.4. Составить систему независимых уравнений для полного анализа цепи по рис. 1.7, а.
РЕШЕНИЕ. В схеме два узла и три главных контура, поэтому по первому закону Кирхгофа нужно составить одно уравнение, а по второму – три. Для узла а имеем:
Уравнения для главных контуров (рис. 1.7, а и 1.8, а):
Выбирая в качестве независимых переменных токи ветвей, переписываем уравнения для контуров с учетом компонентных уравнений табл. 1.1:
ЗАМЕЧАНИЕ. Для схем, которые изображаются на плоскости чертежа без пересечения ветвей (их называют планарными), в качестве главных контуров проще всего выбирать элементарные ячейки, образованные ветвями. Схемы рис. 1.7 и их графы – планарные, поэтому в приведенном примере в качестве третьего главного контура можно было принять ячейку, образованную ветвями 3 и 4, уравнение которой Если ввести в рассмотрение векторы (столбцовые матрицы) для токов и напряжений ветвей
то систему независимых структурных уравнений можно записать в матричной форме: (A)(i) = 0 – первый закон Кирхгофа для узлов; (1.8) (Q)(i) = 0 – первый закон Кирхгофа для главных сечений; (1.9) (B)(u) = 0 – второй закон Кирхгофа для главных контуров. (1.10)
|
|||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 383; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.21.127.68 (0.016 с.) |
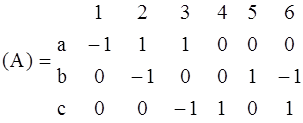
 ;
;  .
. ПРИМЕР 1.3. По заданной контурной матрице (В) нарисовать граф цепи.
ПРИМЕР 1.3. По заданной контурной матрице (В) нарисовать граф цепи.
 , (1.2, а)
, (1.2, а) .
. ;
; ;
;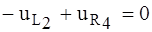 .
.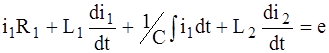 ;
; ;
; .
. . Выбор направления обхода ячеек – произвольный.
. Выбор направления обхода ячеек – произвольный. ;
;  ,
,


