
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
В. А. Долгоруков, Г. С. НечипорукСтр 1 из 6Следующая ⇒
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ Рязанский институт (филиал) Государственного образовательного учреждения высшего профессионального образования «Московский государственный открытый университет» В. А. Долгоруков, Г. С. Нечипорук Статически определимые Стержневые системы в примерах Методические указания для студентов строительных специальностей Рязань УДК 539.3 Н – 59
Рецензенты: профессор кафедры сопротивления материалов и строительной механики МГОУ, к.т.н. Э. Р. Даниелов; доцент кафедры промышленного и гражданского строительства РИ(ф) МГОУ, к.т.н. В. А. Биленко.
Печатается по решению методического совета вуза
Статически определимые стержневые системы в примерах. Методические указания для студентов строительных специальностей. Составители: В. А. Долгоруков, Г. С. Нечипорук. - Рязанский институт (филиал) Государственного образовательного учреждения «Московский государственный открытый университет», 2010
В методических указаниях даны необходимые сведения о методах расчета статически определимых стержневых систем (многопролетных балок, ферм, арок и рам) на неподвижную и подвижную нагрузки и приведены примеры по определению внутренних усилий и перемещений. Даны схемы и исходные данные для выполнения расчетно-графических работ.
© Рязанский институт (филиал) МГОУ, 2010
Оглавление 1.Статически определимые многопролетные балки………………………………3 2. Статически определимые фермы……….……..………………...…………..…17 3. Статически определимые арки…….. …………………………..……………...29 4. Расчет на прочность и жесткость ломаных стержней…………..…………….50 5.Список рекомендуемой литературы…...……………………….………………57 Приложения ………………………………..……………………………………....58 Задание к расчетно-графической работе № 1 (многопролетная балка)……….59 Задание к расчетно-графической работе № 2 (статически определимая ферма)61 Задание к расчетно-графической работе № 3 (статически определимая ферма)64 Задание к контрольной работе (статически определимая рама)……………..….69
Статически определимые многопролетные балки Общая теории линий влияния
1.1.1 Понятие о линиях влияния При расчете мостов, кранов и других инженерных сооружений часто приходится иметь дело с подвижной нагрузкой различного вида. Обычно подвижная нагрузка состоит из системы параллельных друг другу (чаще вертикальных) грузов, между которыми сохраняется неизменное положение. Примерами такой нагрузки являются поезд, перемещающийся по железнодорожному мосту, кран, движущийся по подкрановой балке, и др. Усилия в том или ином элементе сооружения (а также его деформации) зависят от положения подвижной нагрузки. Для определения расчетных величин усилий необходимо из всех возможных положений нагрузки выбрать такое, при котором рассчитываемый элемент будет находиться в наиболее неблагоприятных условиях. Такое положение нагрузки называется невыгоднейшим, или опасным. Указанные выше задачи позволяют решать линии влияния. Линия влияния это график, выражающий изменение той или иной величины (опорной реакции, внутреннего усилия, перемещения в заданном сечении и т. п.) от положения движущегося по сооружению единичного груза постоянного направления.
На рис. 1. 1 для примера показана линия влияния прогиба в сечении «с» при перемещении груза Р = 1 по сооружению. Линию влияния необходимо отличать от эпюры. Это противоположные друг другу понятия. Действительно, ординаты эпюры характеризуют распределение изучаемого фактора (например изгибающего момента) по различным сечениям балки при неподвижной нагрузке; ординаты линии влияния, наоборот, характеризуют изменение фактора (например того же момента), возникающего в одном определенном сечении при перемещающейся по длине балки силы Р = 1. Зная линию влияния какой-либо искомой величины нетрудно определить ее значение при действии системы сосредоточенных грузов, распределенной нагрузки или сосредоточенного момента.
а) влияние системы сосредоточенных грузов (рис. 1. 2). Пусть имеем систему сосредоточенных грузов Р 1, Р 2,…. Рn. Требуется определить влияние этой нагрузки на величину Z, для которой известна линия влияния. Влияние каждой из сил выражается произведением Pi∙yi. Пользуясь принципом независимости действия сил можем записать
Z = P 1 ∙y 1 + P 2 ∙y 2 +……+ Pn∙yn = б) влияние сосредоточенного момента M (рис. 2. 3). Любой момент можно заменить парой сил, расположенных на плече h. Тогда его влияние можно оценить по следующей формуле Z = M (y лев – y пр)/ h., или Z = M∙ tgφ, где φ – угол наклона касательной к линии влияния Z в точке приложения М.
в) влияние распределенной нагрузки (рис. 1. 3). Элементарная сила q ∙ dx будет вызывать элементарное усилие dZ = q ∙ dx ∙ y. Тогда полное усилие Z определится как
В случае равномерной нагрузки при q = const
1.1.2 Построение линий влияния в простой балке Построение линий влияния опорных реакций.
Для построения линии влияния какого-либо параметра необходимо получить формулу (выражение) этого параметра. Запишем выражение для реакции Ra S MB = 0. RAl – P (l – x) = 0.
л. в. при х = 0 Ra = 1, при х = l Ra = 0. Линия влияния реакции Ra показана на рис. 1.4. Для построения л.в. RВ запишем выражение этой реакции. S MА = 0. RВl – P∙ x = 0. л. в. при х = 0 RВ = 0, при х = l RВ = 1. Линия влияния реакции RВ показана на рис. 1.4. Построение линий влияния внутренних усилий. Построение линий влияния Qc. Пусть единичная сила находится справа от сечения «с» (рис. 1.5). Тогда, рассматривая левую от сечения часть балки, можем записать Qc = Ra, или л. в. Qc = л. в. Ra, (1.3) получили уравнение правой ветви л. в. Qc,то есть, когда Р = 1 перемещается по балке на отрезке с - В линия влияния поперечной силы повторяет линию влияния реакции RА.
Теперь Р = 1 перемещается слева от сечения «с». Рассмотрим правую часть балки. Qc = - Rв, или л. в. Qc = (- 1)л. в. RВ. (1.4) Получили уравнение левой ветви. В соответствии с полученными уравнениями (1.3) и (1.4) строим линию влияния Qc (рис. 1.5).
Для построения линии влияния изгибающего момента в сечении «С» используем ту же методику, что и при построении л. в. Qc. Пусть Р = 1 перемещается справа от сечения «С». Рассмотрим левую часть балки. Мc = Ra∙а, или л. в. Мc = (л. в. Ra) ∙а, (1.5) Таким образом, правая ветвь линии влияния повторяет линию влияния Ra, с множителем «а» (рис. 1.5). Теперь Р = 1 перемещается слева от сечения «С». Рассмотрим правую часть балки. Мc = RВ∙b, или л. в. Мc = (л. в. RB) ∙b, (1.6) при х = 0 RВ = 0, Мc = 0, при х = а Мc = (л. в. RB) ∙b = (х /l)∙ b = a∙b / l. Линия влияния Мc приведена на рис. 1.5. Отметим, что при построении линий влияния положительные ординаты откладывают выше оси ординат. Линии влияния реакций и поперечных сил безразмерны, поскольку величина единичной силы безразмерна, линии влияния моментов имеют размерность «метр». Линии влияния для консольной балки
Линия влияния реакции Ra Из уравнения равновесия S y = 0, получим Ra = P = 1, т. е. л. в. RB = 1 (см. рис. 1.6 (б)). Линия влияния поперечной силы в сечении «k» Qk. Единичная сила Р = 1 находится справа от сечения «k». Рассмотрим правую часть балки. Qk = P = 1. Далее, Р = 1 слева от сечения «k». Рассмотрим опять правую ненагруженную часть балки. Qk = 0. Линия влияния изгибающего момента в сечении «k» Мk. Пусть Р = 1 справа от сечения «k». Рассмотрим правую часть балки. Мk = P∙х. При х = 0, Мk = 0, при х = а, Мk = 1∙ а = а. Теперь Р = 1 слева от сечения «k». Рассмотрим опять правую ненагруженную часть балки. Мk = 0. Линии влияния Qk и Мk приведены на рис. 1. 6 (в, г).
Пример 1.1. Построить линии влияния реакций и Qk и Мk в шарнирно опертой балке с консолями (рис. 1.7.). Если выбрать начало координат на левой опоре в точке А, то полученные выше выражения для линий влияния в простой балке справедливы и в данном случае. При этом, координата х будет меняться от – с до l + d.
Дополнительно необходимо построить линии влияния поперечной силы для двух соседних сечений – одно слева от опоры А, другое справа от той же опоры.
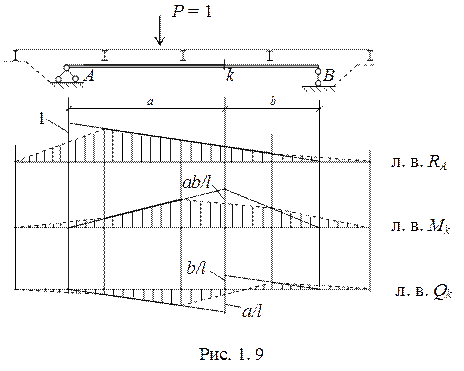
1.1.3 Построение линий влияния при узловой передаче нагрузки. Часто нагрузка передается на конструкцию не непосредственно, а через систему статически определимых балок (настилов) (рис. 1.8). Когда единичный груз находится в начале (т m) или в конце балки (т. n) то он полностью передается на основную конструкцию и вызывает усилия или ym или yn. При движении единичной силы внутри вспомогательной балки ее действие на конструкцию осуществляется через опорные реакции Rm и Rn. Общее влияние в этом случае можно записать как:
Zk = Rm∙ym + Rn∙yn. В свою очередь сами реакции равны (они определяются как в обычной балке)
получили уравнение прямой. При х = 0 Zk = ym, при x = d Zk = yn. Прямая, соединяющая ординаты ym и yn называется передаточная прямая. В качестве примера на рис. 1.9 показаны линии влияния при узловой передаче нагрузки в пролетном строении моста.
1.1.4 Кинематический метод построения линий влияния При расчете многопролетных балок аналитический метод построения линий влияния достаточно громоздок. В таких случаях наиболее удобен кинематический метод, основанный на принципе возможных перемещений - если система находится в состоянии равновесия, то сумма возможных работ всех внешних и внутренних сил на всяком возможном бесконечно малом изменении перемещений равна нулю.
На основании этого принципа можно записать (рис. 1.10, б) - X∙ d xx + 1∙d px = 0, X = d px/ d xx. d xx – постоянная величина, d px – переменная, зависит от х, следовательно л. в. Х = (л. в. d px)/ d xx. d px = х∙tg a, d xx = l∙tg a, тогда Аналогично получаем линию влияния RВ (рис. 1.10, в) путем вертикального смещения опоры B на единицу.
При построении линий влияния Q и М необходимо убрать связи, воспринимающие соответственно поперечную силу и изгибающий момент. Известно, что для соединения в неподвижную систему двух дисков (стержней) достаточно трех связей (рис.1.11). Если убрать 2-ю связь, то данное сечение не будет воспринимать поперечную силу, а вертикальные кромки (торцы) левого и правого стержней будут смещаться параллельно друг другу.
Для построения линии влияния поперечной силы в сечении k Qk двухопорной балки (рис. 1.12) убираем 2-ю связь и даем торцам взаимное вертикальное смещение на единицу, приложив в районе торцов малые положительные поперечные силы (рис. 1.12, б). Отметим, что если при взаимном смещении торцы стержней параллельны, то параллельны друг другу левый и правый стержни целиком. На рис. 1.12, в показан вид линии влияния Qk.
Если убрать в рассматриваемом сечении (рис. 1.11) 1-ю или 3-ю связь, то жесткое соединение превратится в шарнирное, поскольку в этом случае торцы могут свободно поворачиваться относительно друг друга. Такое сечение не воспринимает изгибающий момент. Врезав в сечении k шарнир (рис. 1.12, г) и задав единичное угловое смещение, приложив малые положительные моменты, можем записать работу сил на возможных перемещениях - Рх d x + mk (a + b) = 0, Так как a и b малы, можем записать:
При x = b d x = d k, mk = ab/l. Таким образом, эпюры возможных перемещений, дают вид линии влияния Мk (рис. 1.12, д). Для консольной балки линии влияния, полученные кинематическим способом, имеют вид, показанный на рис 1.13.
1.2 Расчет статически определимых многопролетных балок на Из уравнения равновесия S y = 0 получим: N 97sina = 0, откуда N 97 = 0. Запишем второе уравнение равновесия: S x = 0, - N 97cosa - N 98 = 0, тогда N 98 = 0. Таким образом, оба усилия, сходящиеся в двухстержневом ненагруженном узле, нулевые.
Рассмотрим равновесие 8-го узла (рис. 2.4). Это так называемый трехстержневой узел с единственно выходящим стержнем. Им является стержень 8–7. Записав сумму проекций S y = 0, нетрудно убедиться, что стержень 8–7 — нулевой, а из уравнения S х = 0 следует, что N 98 = N 86. Мысленно вырежем узел 7. С учетом того, что стержень 7–8 нулевой, 7-й узел можно рассматривать как трехстержневой с единственно выходящим стержнем 7–6, который тоже будет нулевым. Остальные узлы либо нагружены, либо не могут рассматриваться как трехстержневые, и в остальных стержнях решетки будут возникать продольные усилия. Пример 2. 2 Вычислить усилия в отмеченных стержнях фермы (рис. 2.5). Наметим путь решения задачи. Усилие в стержне 3–4 удобно искать, рассмотрев равновесие узла 3; усилие в стержне 5–6 проще найти методом вырезания узла 6, а усилие в раскосе 4–5 удобнее находить, используя метод проекций. Для этого необходимо найти реакции опор и провести сечение I–I. S m 1 = 0. P∙ 6– R пр ∙ 12 = 0, R пр = R л = Р /2. Для определения усилия в стержне 3–5 можно воспользоваться методом моментной точки, которая находится в месте пересечения двух других усилий, оказавшихся в сечении I–I. Моментной точкой для N 35 служит узел 4 (рис. 2.5, б).
Дальнейшее решение задачи предлагается провести студентам самостоятельно. Вырезав узел 3, получим N 34 = 0; вырезав узел 6, нетрудно убедиться, что стойка 5–6 сжата усилием P (N 56 = - Р), а спроектировав все силы, приложенные к левой или правой частям фермы на вертикальную ось, получим усилие в раскосе N 54 = R л/cosa = 0,5 P /0,8 = = 0,625 P. Записав уравнение моментов для левой части фермы относительно узла 4, найдем N 35 = R л3/4 = 0,375 Р.
Пример 2. 3. Определить усилия в стержнях третьей панели заданной фермы (рис. 2.6, а). При расчетах принять: d = 3,6 м, h = 3 м, h 1 = 0,4 h = 1,2 м и Р = 80 кН.
Итак, нам необходимо определить усилия в пяти стержнях фермы: в стержнях верхнего и нижнего пояса 5–7 и 4–6, в раскосе 4–7, в левой 4–5 и правой 6–7 стойках третьей панели. Предварительно вычислим ряд геометрических параметров заданной фермы, обозначив размер h - h 1 = h 2.
cosa = d / l 57 = 3,6/3,71 = 0,97, sina = (h 2/2)/ l 57 = 0,9/3,71 = 0,242; tga = 0,9/3,6 = 0,25; с = h 1/tga = 1,2/0,25 = 4,8 м; cosb = d / l 47 = 3,6/4,17 = 0,863; sinb = (h 1 + h 2/2)/ l 47 = 2,1/4,17 = 0,504.
1. Определяем опорные реакции. S mA = 0. - P∙d - P∙ 2 d - P∙ 3 d - P∙ 4 d + RВ∙ 4 d = 0; RВ = 200 кН. В силу симметрии RА = RВ = 200 кН.
2. Для определения усилий в стержнях 4-6, 4-7 и 5-7 разрежем третью панель сечением I-I и рассмотрим равновесие одной из частей фермы под действием внешних и внутренних сил (рис. 2.6, б). Рассматривая правую часть фермы, видим, что для определения N 46 удобно записать уравнение моментов относительно моментной точки 7 (узла 7), в которой пересекаются два других неизвестных усилия N 47 и N 57. S m 7=0. - P∙d + Rb∙d - N 46(h 1+ h 2/2) = 0. N 46 = (- 80×3,6 + 200×3,6)/2,1 = 206 кН. Усилие N 46 направлено на чертеже от узла и получилось положительным, следовательно, стержень 4-6 растянут. Для определения усилия N 57 также удобно использовать метод моментной точки (узел 4). Рассмотрим равновесие левой части фермы. S m 4 = 0. – Rа∙ 2 d + P∙ 2 d + P∙d - (N 57cosa) h = 0. N 57 = (- 200 ∙ 7,2 + 80 ∙ 7,2 + 80 ∙ 3,6)/(0,97×3) = - 198 кН.
Знак «-» у усилия N 57 говорит, что стержень 5-7 сжат. Усилие N 47 можно найти либо методом проекций на ось у всех сил, приложенных к одной из частей фермы, либо методом моментной точки. В данном случае это будет точка m, лежащая справа от опоры В (рис. 2.6). Воспользуемся методом проекций, рассмотрев равновесие левой части фермы (рис. 2.6, б). S y = 0. RА - P - P - P - N 57sina + N 47sinb = 0. N 47 = [- 200 + 80 + 80 + 80 + (- 198) ∙ 0,242]/0,504 = - 15,7 кН (стержень сжат).
Для вычисления усилия в стержне 6-7 проведем сечение II-II (рис. 3.32, а) и рассмотрим равновесие правой части фермы (рис. 2.7). Воспользуемся методом моментной точки: для усилия N 67 моментной точкой будет точка m, в которой пересекаются два других усилия N 46 и N 78. S mm = 0, - N 67(d + c) + Pc - Rbc = 0. N 67 = (80 ∙ 4,8 - 200 ∙ 4,8)/8,4 = - 69 кН, (стержень 6-7 сжат).
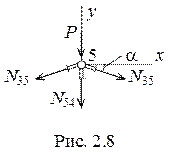
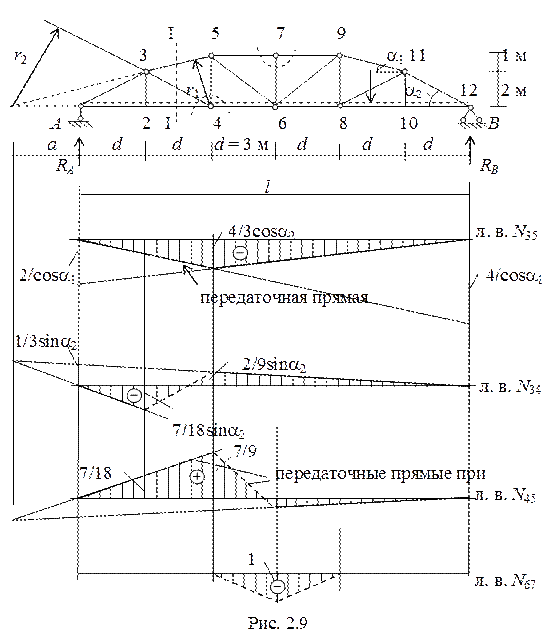
В стойке 5-6 усилие будем определять методом вырезания узлов, вырезав узел 5 (рис. 2.8). Спроецируем все усилия, сходящиеся в узле, на ось у. В силу симметрии фермы и внешней нагрузки усилие в стержне 3-5 примем равным усилию в стержне 5-7. S y = 0. - P - N 45 - N 57sina - N 35sina = 0; N 45 = - 80 -2(-198) ∙ 0,242 = 15,8 кН, cтойка 4 - 5 растянута. Для проверки полученных усилий можно записать уравнение проекций всех сил, приложенных к левой или правой частям фермы (рис. 2.6, б) на ось х. S x = 0. N 57cosa + N 47cosb + N 46 = 0; (- 198) ∙ 0,97 + (-15,7) ∙ 0,863 + 206 = - 205,6 + 206 = 0. Погрешность d, полученная в результате проверки, равна: d = (206 - 205,6) ∙ 100%/205,6 = 0,2%, при допустимой (разрешенной) для данного типа задач 3-5%. 2.3 Расчет ферм на подвижную нагрузку Расчет ферм на подвижную нагрузку сводится к построению линий влияния при действии на ферму подвижной единичной силы, перемещающейся по одному из поясов. Порядок построения линий влияния в фермах рассмотрим на примере. Рассмотрим построение линий влияния усилий N 35, N 34, N 45, и N 67 для фермы, показанной на рис. 2. 9.
Для построения линии влияния (а это график) усилия в стержне 3-5 необходимо получить выражение для этого усилия в зависимости от положения единичной силы. В свою очередь, единичная сила Р = 1 перемещается по нижнему поясу – это отмечено пунктирной линией. Для определения усилия N 35 разрежем вторую панель сечением I-I и воспользуемся методом моментной точки. Моментной точкой является узел 4. Пусть единичная сила перемещается справа от разрезанной панели между 4 и 12 узлами. Рассмотрим равновесие левой части фермы. S m 4= 0, RА ∙2 d + N 35∙ r 1= 0. (r 1 = h cosa1)
л. в. N 35 = Для построения правой ветви линии влияния N 35 отложим на левой опорной вертикали ординату 1∙2/cosa1. Поскольку линия влияния имеет знак минус, указанную ординату откладываем вниз. Правая ветвь будет проходить от 12 до 4 узла. Р =1 находится слева от разрезанной панели между 1 и 2 узлами. Рассмотрим равновесие правой части фермы. S m 4= 0, RВ ∙4 d + N 35∙ r 1= 0. По аналогии л. в. N 35 = Откладывая на правой опорной вертикали ординату 1∙4/cosa2, строим левую ветвь линии влияния N 35 от 1 до 2 узла. Движение единичной силы между 2 и 4 узлами можно осуществить по настилу. В этом случае будет иметь место узловая передача нагрузки, а линия влияния будет очерчена передаточной прямой (пунктирной линией), соединяющей левую и правую ветви. Отметим, что левая и правая ветви пересекаются под моментной точкой. Это свойство линий влияния можно использовать для проверки. Построим, используя приведенную выше методику, линию влияния усилия N 34. Моментная точка для этого усилия находится в точке «к», в точке пересечения продолжения стержней 2-4 и 3-5. Из подобия треугольников находим, что а = d = 3 м, плечо у усилия N 34 относительно моментной точки составит r 2 = 3 d∙ sina2. Р = 1 справа от разрезанной панели. S m к= 0, RА ∙ а - N 34∙ r 2= 0. л. в. N 34 = Строим правую ветвь, отложив на левой опорной вертикали 1/3sina2. Ординату под 4 узлом (2/9sina2) находим из подобия треугольников. Р = 1 слева от разрезанной панели. S m к= 0, RВ ∙7 d + N 34∙ r 2= 0. л. в. N 34 = Строим левую ветвь, отложив вниз на правой опорной вертикали 7/3sina2. В районе второго узла ордината составит 1/6 от 7/3sina2. Передаточной прямой соединяем левую и правую ветви. Не трудно убедиться, что они пересекаются под моментной точкой. Для определения усилия N 45 и построения его линии влияния можно так же воспользоваться методом моментной точки (точка «к») или методом вырезания узлов. Действительно, вырезав узел 4 (рис. 2.10) можно увидеть что в уравнение S у = 0 входит одно неизвестное N 45. Линия влияния усилия N 34 нами получена.
Рассмотрим равновесие 4 узла. S у = 0. N 34sina2 + N 45 = 0. N 45 = - N 34sina2, или л. в. N 45 = - (л. в. N 34)∙sina2 Вырезая узел 4, нам пришлось разрезать вторую и четвертую панели, т. е. левая ветвь линии влияния проходит от1 до 2 узла, а правая от 6 до 12 узла. Строим эти ветви. В качестве промежуточного будет положение единичной силы в 4 узле (рис. 2.11). В этом случае S у = 0. N 34sina2 + N 45 – Р = 0. N 45 = - N 34sina2 + 1 = - Откладываем в районе 4 узла 7/9 и проводим две передаточные прямые. Получили линию влияния N 45. Необходимо обратить внимание где пересекаются левая и правая ветви линии влияния N 45. При езде понизу усилие в стержне 6-7 равно нулю – стержень 6-7 нулевой. В то же время, при езде поверху при движении единичной силы между 5 и 9 узлами в стойке 6-7 будет возникать нагрузка. При движении по остальной части верхнего пояса стержень 6-7 остается нулевым, следовательно левая (от 1 до 5 узла) и правая (от 9 до 12 узла) ветви линии влияния усилия N 67 тоже нулевые. Воспользуемся методом вырезания узлов, когда сила Р = 1 находится в 7 узле (рис. 2. 12). S у = 0. – N 67 – Р = 0.. N 67 = – 1. Откладываем ординату (– 1) от проекции 7 узла, проводим передаточные прямые и получаем линию влияния N 67. 3. Трехшарнирные арки Арочными называются системы криволинейного или ломаного очертания, в опорах которых от вертикальной нагрузки возникают наклонные реакции, направленные, как правило, внутрь пролета. Горизонтальная составляющая такой наклонной реакции называется распором. Арочные системы в сравнении с балочными оказываются экономически более выгодными за счет меньших, чем в балках, изгибающих моментов.
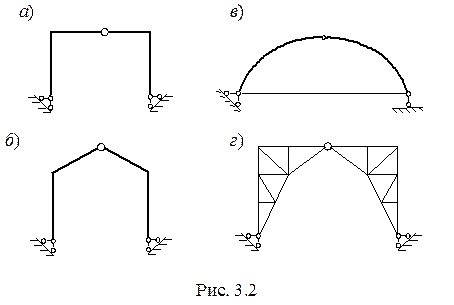
Двухшарнирные и безшарнирные арки являются статически неопределимыми и будут рассматриваться в соответствующем разделе. Трехшарнирная арка является системой геометрически неизменяемой и статически определимой. Принятые обозначения в арках показаны на рис. 3.1. В практике встречаются различные по форме и виду арки. В том случае, когда каждая половина трехшарнирной арки представляет собой сплошной брус криволинейного очертания, ее называют аркой со сплошной стенкой (рис. 3.1). При ломаном очертании оси сооружение обычно называют трехшарнирной рамой (рис. 3.2, а, б). Система, изображенная на рис. 3.2, в, носит название трехшарнирной арки с затяжкой.
В практике встречаются арки, образованные из двух ферм, соединенных между собой общим шарниром (рис. 3.2, г). Такие системы называются трехшарнирными фермами. 3.1 Аналитический расчет трехшарнирной арки Определение опорных реакций
При действии внешней нагрузки на трехшарнирную арку (рис. 3.3) в каждой ее опоре возникает по две реакции. Всего, таким образом, имеется четыре неизвестные реакции – две вертикальные RA, RB и две горизонтальные НA и НB. Для расчета трехшарнирной арки кроме трех уравнений равновесия, которые дает статика для системы сил, расположенной в одной плоскости, можно составить четвертое уравнение, основанное на том, что сумма моментов всех сил, приложенных по одну сторону от ключевого шарнира С, равна нулю. Действительно, это уравнение для изгибающего момента в поперечном сечении, а в шарнире момент отсутствует. Для трехшарнирной арки (рис. 3.3) при определении реакций будут записаны следующие уравнения: S mB = 0, - RAl + P 1(l – a 1) + P 2 a 2 = 0, (а) RA = [ P 1(l – a 1) + P 2 a 2]/ l. S mA = 0, RBl – P 1 a 1 – P 2(l – a 2) = 0, (б) RB = [ P 1 a 1 + P 2(l – a 2)]/ l. Уравнения (а) и (б) для вычисления вертикальных реакций имеют тот же вид, что и уравнения в балочной системе. Для вычисления распора запишем следующие уравнения: S x = 0, HA – HB = 0, HA = HB = H. S mC пр = 0, RBl 2 – P 2(l 2 – a 2) – HBf = 0, (в) HB = H = [ RBl 2 – P 2(l 2 – a 2)]/ f, или:
В выражении (3.1) МС бал представляет собой изгибающий момент в сечении С в балке, перекрывающей тот же пролет и воспринимающей заданную на трехшарнирную арку вертикальную нагрузку (рис. 3.3). Из формулы (3.1) следует, что величина распора Н обратно пропорциональна стреле подъема арки f.
Определение внутренних усилий в арке от вертикальной нагрузки При действии на арку только вертикальных нагрузок (рис. 3.4, а) изгибающий момент в сечении с абсциссой х равен: Mx = RAx – P 1(x - a 1) – P 2(x - a 2) – Hy, или: Мx = Mx бал - H ∙ y, (3.2) где Мх бал — изгибающий момент в балке (рис. 3.4, б) от той же нагрузки в сечении с абсциссой х (так называемый балочный момент). Формулой (3.2) удобно пользоваться при построении эпюры моментов в арке. Значения Мх бал непосредственно берут из эпюры моментов, построенной для балки. Величину распора находят по формуле (3.1). Полученная формула для Мх наглядно показывает уменьшение изгибающего момента в арке по сравнению с балкой, что подтверждает экономичность арочной конструкции по сравнению с балочной. Это видно из построений на рис. 3.4, г, где показано совмещение балочной эпюры моментов и кривой, соответствующей слагаемому Н∙у в формуле (3.1). На рис. 3.4, д показан вид эпюры моментов Мх в арке.
Аналогичные формулы можно получить для поперечной Qx и продольной Nx сил. Для этого спроецируем все приложенные слева от сечения n – n силы (рис. 3. 4, в) сначала на нормаль к оси арки в сечении с абсциссой х, а затем на касательную к ней:
Qx = (RA – P 1 – P 2)cosj x – H sinj x, Nx = + (RA – P 1 – P 2)sinj x + H cosj x. Нетрудно убедиться, что величина, стоящая в круглых скобках в записанных выше выражениях, представляет собой величину поперечной силы в балке в сечении с той же абсциссой х; тогда эти формулы примут вид: Qx = Qx бал cosj x - Н sinj x, (3.3) Nx = Qx бал sinj x + H cosj x. (3.4) Отметим, что в арке принято считать N > 0 при сжатии. Рациональная ось арки Из формулы (3.2) следует, что в том случае, когда очертание оси арки совпадает с очертаниями балочной эпюры моментов М бал, называемой кривой давления, т. е. если
то в такой арке изгибающий момент Мх = 0.
Уравнение (3.5) называют уравнением рациональной оси арки. На рис. 3. 5, в приведены очертания арок с рациональной осью для различных случаев нагружения. Пример 3.1 Для заданной трехшарнирной арки с размерами, показанными на рис. 3. 6, вычислить значения внутренних усилий в сечениях m и n. Построить эпюры внутренних усилий. Уравнение оси арки – квадратная парабола с началом координат в точке А:
1. Определяем опорные реакции: S mA = q 6×3 + P∙ 9 – RB 12 = 0. RB = 6 кН. S mB = q 6×9 + P∙ 3 – RA 12 = 0. RA = 10 кН. H = MC бал/ f = (RB 6 – P∙ 3)/4 = 6 кН. 2. Строим эпюры Qх бал и Мх бал. 3. По формуле (3.2) вычисляем значения Мх, получив предварительно ординаты заданных сечений m и n:
4. Вычисляем Qm и Qn, используя формулу (3.3) Qm=Qm балcosj m - H sinj m Для вычисления тригонометрических функций воспользуемся следующими математическими соотношениями:
тогда
Аналогично: sinj n = - 0,555, cosj n = 0,832. Подсчитаем значения Q в заданных сечениях: Qm = Qm балcosj m - H sinj m = 4×0,832 – 6×0,555 = 0. В сечении n эпюра Q бал имеет разрыв, аналогично будет разрыв и в эпюре поперечных сил арки. Поэтому необходимо подсчитать поперечную силу слева и справа от сечения:
Одновременно найдем поперечные силы в опорных сечениях А и В.
QA = 10×0,6 – 6×0,8 = 1,2 кН; QB = -6×0,6–6(-0,8) = 1,2 кН. QC = - 2×1 = - 2 кН.
5. Вычисляем продольные усилия по формуле (3.4): Nm = Qm балsinj m + H cosj m = 4×0,555 + 6×0,832 = 7,218 кН,
|
|||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 488; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.205.223 (0.217 с.) |
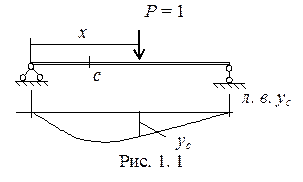

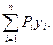




 или
или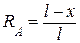 . (1.1)
. (1.1)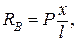 или
или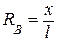 . (1.2)
. (1.2)
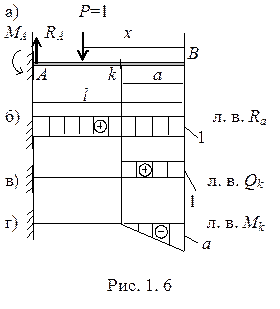


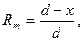
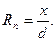 Тогда
Тогда -
-

 , т. е. линия влияния левой реакции RА повторяет эпюру перемещений балки при смещении левой опоры на единицу.
, т. е. линия влияния левой реакции RА повторяет эпюру перемещений балки при смещении левой опоры на единицу.




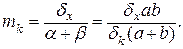



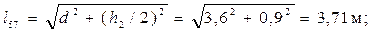


 тогда уравнение правой ветви примет вид линии влияния реакции Ra, умноженной на множитель 2 d / r 1:
тогда уравнение правой ветви примет вид линии влияния реакции Ra, умноженной на множитель 2 d / r 1: (л. в. RА) =
(л. в. RА) =  (л. в. RА) = -
(л. в. RА) = - 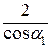 (л. в. RА).
(л. в. RА). (л. в. RВ) =
(л. в. RВ) =  (л. в. RА) =
(л. в. RА) = 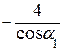 (л. в. RА).
(л. в. RА). (л. в. RА) =
(л. в. RА) =  (л. в. RА) =
(л. в. RА) =  (л. в. RА).
(л. в. RА). (л. в. RВ) =
(л. в. RВ) =  (л. в. RВ).
(л. в. RВ).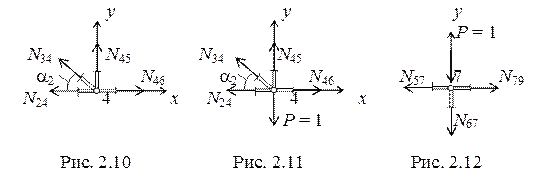
 sina2 + 1 =
sina2 + 1 =  .
.

 (3.1)
(3.1)
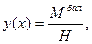 (3.5)
(3.5)
 , где l = 12 м, f = 4 м.
, где l = 12 м, f = 4 м.


 ;
;
 ,
,
 ,
, 
 ,
, ,
, 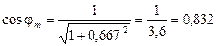 .
.






