
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методы вычисления определителей
Как убедились выше, определители низших порядков (2-го и 3-го) находят, используя определения. Но бывают случаи, когда для вычисления таких определителей сначала лучше использовать свойства. Пример 2.4. Найти определитель 2-го порядка: Решение. Умножим первую строку на (-1) и прибавим ко второй, получим
, Определение определителя n -го порядка, а также свойства легли в основу некоторых методов вычисления определителей 4-го и выше порядков. Рассмотрим эти методы. 1) Используя разложение по строке или столбцу. В результате использования определения определителя n -го порядка мы приходим к вычислению определителей (n -1)-го порядка. 2) Метод эффективного понижения порядка. Используя основные свойства определителей, вычисление 3) Приведение определителя к треугольному виду. Определитель, у которого все элементы, находящиеся выше или ниже главной диагонали, равны нулю, называются определителем треугольного вида. В этом случае определитель равен произведению элементов его главной диагонали. Приведение любого определителя n -го порядка к треугольному виду всегда возможно. 4) Использование программы Excel пакета Microsoft Office. Excel имеет в своем составе большое количество различных функций - предустановленных формул, использующихся для выполнения стандартных вычислений. Для вычисления определителя из математических функций используется МОПРЕД (массив).
Пример 2.5. Найти определитель 4-го порядка используя все три способа:
Решение. 1) Воспользуемся разложением определителя по второй строке, поскольку в этой строке один элемент нулевой. Получаем
2) Воспользуемся приведением определителя к треугольному виду. Умножим вторую строку на (-2) и прибавим к первой строкой, умножим вторую строку на (-3) и прибавим к третьей, умножим вторую строку на (-4) и прибавим к четвертой. Получаем
[складываем вторую и третью строку, вторую строку умножаем на 2 и складываем с четвертой строкой]
[умножаем третью строку на (-11/8) и складываем с четвертой строкой]
3) Используем метод эффективного понижения порядка. Умножим первый столбец на (-2) и прибавим к третьему столбцу, умножим первый столбец на (-1) и прибавим к четвертому столбцу.
[к первой строке прибавим вторую; первую строку умножим на 2 и прибавим третью строку]
=
4) Открываем экран Excel. Последовательно заносим в ячейки элементы определителя в виде массива. Например, ячейки B5:E8 (Рис. 1).
Рис. 1. Внесенные в ячейки элементы определителя Входим в диалоговое окно
Рис. 2. Диалоговое окно Мастер функций В результате появляется окно Аргументы функции, где в ячейку Массив вносим выделенный массив элементов определителя: B5:E8 (Рис. 3). Внизу этого окна появляется значение 23.
Рис. 3. Диалоговое окно Аргументы функции Если нажать на ОК, то в выделенной ячейке появится 23. ,
3. ОБРАТНАЯ МАТРИЦА
3.1. Теорема существования обратной матрицы
Определение 3.1. Квадратная матрица A называется невырожденной, если ее определитель Определение 3.2. Матрицей, присоединенной к матрице A, называется матрица вида
где Определение 3.3. Матрица
где E – единичная матрица того же порядка, как и матрица A.
Матрица
Пример 3.1. Показать,что матрица A является обратной для матрицы B, если
Решение. Найдем произведение матриц A и B.
Аналогично , Теорема 3.1. Для невырожденной матрицы A существует единственная обратная матрица
где Доказательство. 1) Сначала докажем существование единственной обратной матрицы. Пусть
Таким образом,
2) Используя равенство (3.1) докажем справедливость формулы (3.2). Покажем, что
Аналогично убеждаемся, что , Пример 3.2. Найти Решение. 1) Находим определитель матрицы A.
Матрица A – невырожденная, значит, существует ей обратная. 2) Находим алгебраические дополнения элементов матрицы A.
Составляем матрицу, присоединенную к матрице A.
3) Находим
Сделаем проверку:
,
|
||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 493; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.213.209 (0.015 с.) |
 .
. .
. всегда можно свести к вычислению одного определителя (n -1)-го порядка, сделав в каком-либо ряду
всегда можно свести к вычислению одного определителя (n -1)-го порядка, сделав в каком-либо ряду 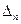 все элементы, кроме одного, равными нулю.
все элементы, кроме одного, равными нулю. .
.

 .
.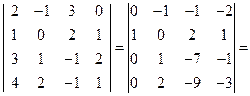 [поменяем местами первую и вторую строку]
[поменяем местами первую и вторую строку] 

 .
.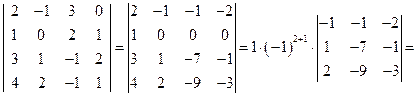
 .
.
 - Мастер функций. Выбираем категорию: математические функции. Из предложенных выбираем функцию МОПРЕД (массив). Нажимаем ОК (Рис. 2).
- Мастер функций. Выбираем категорию: математические функции. Из предложенных выбираем функцию МОПРЕД (массив). Нажимаем ОК (Рис. 2).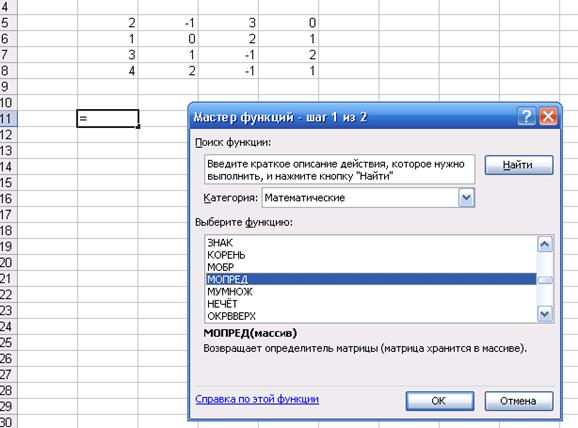

 . В противном случае матрица A называется вырожденной или особенной.
. В противном случае матрица A называется вырожденной или особенной. ,
, - алгебраическое дополнение элемента
- алгебраическое дополнение элемента  данной матрицы A (оно определяется так же, как и алгебраическое дополнение элемента определителя).
данной матрицы A (оно определяется так же, как и алгебраическое дополнение элемента определителя). называется обратной матрице A, если выполняется условие
называется обратной матрице A, если выполняется условие , (3.1)
, (3.1) .
. .
. . Следовательно, матрица A является обратной для B.
. Следовательно, матрица A является обратной для B. , (3.2)
, (3.2) - матрица, присоединенная к матрице A.
- матрица, присоединенная к матрице A.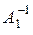 и
и  - матрицы, обратные для матрицы A. Тогда, используя свойство умножения матрицы на единичную матрицу, свойство ассоциативности и равенства (3.1), получаем следующее
- матрицы, обратные для матрицы A. Тогда, используя свойство умножения матрицы на единичную матрицу, свойство ассоциативности и равенства (3.1), получаем следующее .
. .
. . В ходе преобразований будем использовать свойство 9 для определителей и разложение определителя n- го порядка по i -ой строке.
. В ходе преобразований будем использовать свойство 9 для определителей и разложение определителя n- го порядка по i -ой строке.
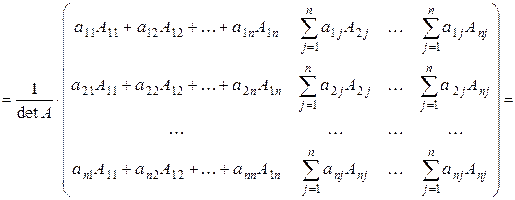
 .
. .
. .
. .
. .
.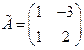 .
. .
.



