
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дійсні числа. Модуль числа та його властивості.
Дійсним числом називається будь-який десятковий дріб, скінчений чи нескінчений. Якщо Множина дійсних чисел Множина дійсних чисел Надалі, у випадках коли належність чи неналежність множині граничних точок Інтервал Для позначення відстані довільної точки Означення. Модулем числа
Наприклад: Властивості модуля: 1. 3. 5. 7. Нерівність
Означення та способи задання функції. Графік функції. Нехай задано множину чисел Множина З означення функції випливає, що функція вважається заданою, якщо вказано закон відповідності і область визначення. Якщо область визначення функції Приклад 1.1. Знайти область визначення функції Розв’язування. Очевидно, що вираз
Нехай функція
Графіком функції Функція може бути задана одним з основних способів: аналітичним, табличним або графічним. Вважають, що функція Нехай на площині дано прямокутну систему координат Функцію можна задати і за допомогою таблиці, в одному рядку якої записані значення однієї величини, а в іншому – відповідні значення другої величини, що залежить від першої. Зауваження. Якщо функція задана аналітично, то неважко перейти до табличного або графічного способу задання функції. Перехід від табличного або графічного способів задання функцій до аналітичного вимагає певних знань та навичок.
Завдання для самостійного розв’язування. 1.1 Знайти область визначення функцій: а) в) Відповіді: 1.1 а) в) Складена функція. Нехай функція Наприклад, функція Проте може статись так, що
|
|||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 431; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.139.240.142 (0.01 с.) |
 – деяка множина дійсних чисел, то запис
– деяка множина дійсних чисел, то запис  означає, що число
означає, що число  належить
належить 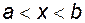 (
( ), де
), де  – фіксовані числа, називається інтервалом (відрізком) і позначається
– фіксовані числа, називається інтервалом (відрізком) і позначається  (
( ).
). або
або  , називається півінтервалом.
, називається півінтервалом. немає суттєвого значення, інтервал, відрізок, півінтервал будемо називати проміжком і позначати
немає суттєвого значення, інтервал, відрізок, півінтервал будемо називати проміжком і позначати  .
. ,
,  називається
називається  – околом точки
– околом точки  .
. – модуль числа.
– модуль числа.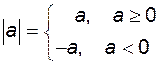
 .
. 2.
2. 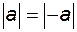
 4.
4. 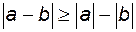
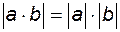 6.
6. 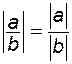
 означає, що
означає, що 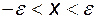 .
. , якщо кожному
, якщо кожному  і записують
і записують 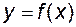 . При цьому
. При цьому  або
або  ,
,  всіх таких значень – областю значень функції і позначається
всіх таких значень – областю значень функції і позначається  або
або 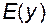 .
.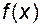 має значення, то таку область визначення будемо називати максимальною областю визначення або областю існування. В подальших прикладах знаходження області визначення функції пов’язане тільки із знаходженням області існування.
має значення, то таку область визначення будемо називати максимальною областю визначення або областю існування. В подальших прикладах знаходження області визначення функції пов’язане тільки із знаходженням області існування. .
. має сенс тоді і тільки тоді, коли
має сенс тоді і тільки тоді, коли  , або
, або 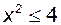 . Так як
. Так як  , то
, то  . Згідно властивості 7 модуля
. Згідно властивості 7 модуля  . Отже, область визначення функції є відрізок
. Отже, область визначення функції є відрізок 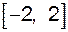 .
. – на множині
– на множині  . Якщо переріз
. Якщо переріз  не є порожня множина, то на цьому перерізі можна визначити суму
не є порожня множина, то на цьому перерізі можна визначити суму  , різницю
, різницю  , добуток
, добуток  і частку
і частку  двох функцій (останню лише при умові
двох функцій (останню лише при умові  ).
). площини
площини  , координати яких пов’язані даною функціональною залежністю. Найчастіше функція задається на проміжку
, координати яких пов’язані даною функціональною залежністю. Найчастіше функція задається на проміжку  , перетинає цю криву не більше ніж в одній точці. Це графічний спосіб задання функції.
, перетинає цю криву не більше ніж в одній точці. Це графічний спосіб задання функції.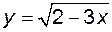 ; б)
; б)  ;
; ; г)
; г)  ;
; б)
б) 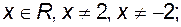
 г)
г) 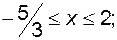
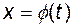 на множині
на множині  , причому для всіх
, причому для всіх  відповідне значення
відповідне значення  належить множині
належить множині  , що називається складеною функцією від
, що називається складеною функцією від  , або суперпозицією функцій
, або суперпозицією функцій  і
і  визначена на множині
визначена на множині  , а функція
, а функція  визначена на множині
визначена на множині 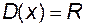 і має область зміни
і має область зміни  . Так як множина
. Так як множина  , то суперпозиція цих функцій
, то суперпозиція цих функцій  визначена на множині
визначена на множині  .
. не мають спільних точок, тоді відповідні функції
не мають спільних точок, тоді відповідні функції  і
і  такі, що
такі, що  і
і  не мають ні однієї спільної точки. Таким чином, вираз
не мають ні однієї спільної точки. Таким чином, вираз 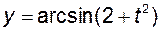 не задає функції від
не задає функції від 


