
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определители второго порядка и их свойстваСтр 1 из 7Следующая ⇒
Действия над матрицами Равенство матриц Две матрицы A и B называют равными, (A=B), если они имеют одинаковое число строк и одинаковое число столбцов и их соответствующие элементы равны:
Сложение матриц Две матрицы одинаковых размеров
Операция сложения матриц обладает следующими свойствами: 1. 2. 3. Пример 1.1. Даны две матрицы А и В. Найти А + В.
Умножение матрицы на число Любую матрицу А можно умножить на число
Операция умножения матрицы на число обладает следующими свойствами: 1. 2. 3. Пример 1.2. Даны две матрицы А и В. Найти -5 А и 2А - В.
Произведение матриц Произведением матрицы
Из определения двух матриц видно, что перемножить можно лишь матрицы, у которых число столбцов первой матрицы сомножителя А равно числу строк второй матрицы сомножителя В. Например, если
Пример 1.3. Даны две матрицы А и В. Найти
Эти примеры показывают, что произведение двух матриц, вообще говоря, не подчиняется переместительному закону: Определение 1.1. Матрицы А и В, для которых АВ=ВА, называются коммутативными. Операция перемножения матриц обладает следующими свойствами: 1. 2.
Сложение матриц Две матрицы одинаковых размеров
Операция сложения матриц обладает следующими свойствами:
4. 5. 6. Пример 1.1. Даны две матрицы А и В. Найти А + В.
Умножение матрицы на число Любую матрицу А можно умножить на число
Операция умножения матрицы на число обладает следующими свойствами: 4. 5. 6. Пример 1.2. Даны две матрицы А и В. Найти -5 А и 2А - В.
Произведение матриц Произведением матрицы
Из определения двух матриц видно, что перемножить можно лишь матрицы, у которых число столбцов первой матрицы сомножителя А равно числу строк второй матрицы сомножителя В. Например, если
Пример 1.3. Даны две матрицы А и В. Найти
Эти примеры показывают, что произведение двух матриц, вообще говоря, не подчиняется переместительному закону: Определение 1.1. Матрицы А и В, для которых АВ=ВА, называются коммутативными. Операция перемножения матриц обладает следующими свойствами: 3. 4. Транспонирование матриц Если строки матрицы А записать в виде столбцов, а столбцы в виде строк, то получим матрицу транспонированную матрицу Операция транспонирования обладает следующими свойствами: 1. 2. 3. 4. Пример 1.4. Дана матрица А. Найти А Т.
Определители второго порядка и их свойства Рассмотрим матрицу второго порядка:
Определение 2.1. Определителем (или детерминантом) второго порядка, соответствующим данной матрице, называется число
Пример 2.1. Вычислить определитель матрицы:
Свойства определителей Сформулируем основные свойства определителя:
Обратная матрица
Понятие обратной матрицы вводится только для квадратных матриц. Определение 3.3. Если А — квадратная матрица, то обратной для нее матрицей называется матрица, обозначаемая А -1и удовлетворяющая условию
Теорема 3.1. (об обратной матрице): Для того, чтобы квадратная матрица А имела обратную, необходимо и достаточно, чтобы матрица А была невырожденной, т. е. чтобы ее определитель был отличен от нуля. Для простоты на примере матрицы третьего порядка приведем последовательность вычислений, которая позволяет построить обратную матрицу. Пусть
Невырожденная матрица, т. е. её определитель
Составим новую матрицу В, заменяя в матрице А каждый ее элемент аij его алгебраическим дополнением Аij, деленным на определитель |A | матрицы А:
Построим матрицу ВТ, транспонированную по отношению к матрице В:
Покажем, что матрица ВТ, является обратной матрице А. Для этого составим произведение:
Так как. числители элементов на главной диагонали равны |A| (раскрытие определителя по элементам строки), а числители всех остальных элементов равны нулю (сумма произведений элементов одной строки или столбца на алгебраические дополнения другой строки или столбца равна нулю). Таким образом,
Пример 3.1. Дана матрица
Найти обратную матрицу. Вычислим определитель матрицы А:
Находим алгебраические дополнения элементов этого определителя по формулам
Следовательно,
11.Элементарные преобразования матриц При вычислении обратной матрицы, как правило, приходится вычислять большое число определителей. Чтобы облегчить этот процесс, применяют специальные приемы, которые называют элементарными преобразованиями матриц. Элементарными называются следующие преобразования: · умножение всех элементов какой-либо строки (столбца) матрицы на одно и то же число, отличное от нуля; · прибавление к элементам какой-либо строки (столбца) матрицы соответствующих элементов другой строки (столбца), умноженных на одно и то же число; · перемена местами строк (столбцов) матрицы; · отбрасывание строк (столбцов) матрицы, все элементы которых равны нулю. Матрицы, получающиеся одна из другой при элементарных преобразованиях, называются эквивалентными. Пример 4.1. Вычислить определитель матрицы:
Преобразуем матрицу так, чтобы не вычислять много миноров. Для этого в первом столбце во второй, третьей и четвертой строках получим нули. Работу начнем со второй строки, первую строку перепишем без изменений. Воспользуемся элементарными преобразованиями матрицы и ко второй строке прибавим первую, умноженную на
Теперь к третьей строке прибавим первую строку, умноженную на
И, наконец, к четвертой строке прибавим первую, умноженную на
Определитель полученной матрицы равен произведению элемента
Пример 4.2. Вычислить определитель матрицы:
Преобразуем матрицу так, чтобы под главной диагональю стояли нули. ПоДля этого в первом столбце во второй, третьей и четвертой строках получим нули. Работу начнем со второй строки, первую строку перепишем без изменений. Воспользуемся элементарными преобразованиями матрицы и ко второй строке прибавим первую, умноженную на
Теперь к третьей строке прибавим первую строку, умноженную на
И, наконец, к четвертой строке прибавим первую, умноженную на Ранг матрицы Рассмотрим матрицу размера
Выделим в ней несколько миноров. Определение 3.1. Наибольший из порядков миноров данной матрицы, отличных от нуля, называется рангом матрицы. Определение 3.2. Минор, порядок которого определяет ранг матрицы, называется базисным. У матрицы может быть несколько базисных миноров. Пример 4.4. Найти ранг матрицы:
Определитель матрицы (3.2) равен нулю. Все миноры 3-го порядка равны нулю, например:
Есть минор 2-го порядка, отличный от нуля:
Значит, Свойства ранга матрицы
Использование этих свойств позволяет в ряде случаев упростить вычисления ранга.
Пример 4.5. Найти ранг матрицы:
Определитель матрицы (4.3) равен нулю, поскольку матрица имеет пропорциональные строки, например, первую и третью. Значит ранг матрицы (4.3) будет меньше 4. Выполним некоторые элементарные преобразования: к третьей строке матрицы прибавим первую строку, умноженную на
Полученная матрица, очевидно, имеет ранг 2. Итак, Метод окаймления При вычислении ранга можно использовать метод окаймления, состоящий в следующем. Пусть матрица Пример 4.6. Найти ранг матрицы, используя метод окаймления:
Эта матрица имеет ненулевой минор
Теперь достаточно рассмотреть не все миноры третьего порядка, а только миноры, которые содержат указанный ненулевой минор второго порядка:
Итак, Система линейных уравнений Система n линейных алгебраических уравнений с n неизвестными имеет следующий вид:
Система линейных уравнений называется совместной, если она имеет решение, и несовместной, если она не имеет решения. Совместная система линейных уравнений называется определенной, если она имеет единственное решение, и неопределенной, если она имеет бесчисленное множество решений. Две совместные системы уравнений называются равносильными, если решение первой системы является решением второй и наоборот. С помощью теорем линейной алгебры можно доказать, что следующие преобразования, которые принято называть элементарными, приводят к равносильным системам: · перемена местами двух любых уравнений; · умножение обеих частей уравнений на произвольное число, отличное от нуля; · прибавление к обеим частям одного из уравнений другого уравнения, умноженного на любое действительное число. Формулы Крамера Рассмотрим еще раз систему n уравнений с n неизвестными
Или
Вспомним, что две матрицы равны, если равны их соответствующие элементы:
Обратим внимание на то, что выражения в круглых скобках равенств (4.13) представляют собой определители, полученные из определителя системы
С учетом этих обозначений формулы (4.13) можно переписать в виде:
Пример 4.2. Решить систему уравнений методом Крамера
Ранее определитель системы
уже был вычислен Вычислим определители неизвестных:
Используя формулы Крамера, найдем:
Множества. Основные понятия Понятие множества является основным, неопределяемым понятием, поэтому можно только пояснить этот термин. Под множеством
Символом Определение 1.1. Множества Записать утверждение о том, что множество
Если множества состоят из разных элементов, то этот факт записывают
Пример 1.1. Даны три множества Пример 1.2. Даны два множества При рассмотрении способов задания множеств возникает проблема их эффективного описания. Частично эту проблему можно решить, если указывать условие, которому удовлетворяет любой элемент данного множества:
Пример 1.3. Множество Зачем? Пример 1.4. Парадокс брадобрея. Владелец парикмахерской в одном селе повесил следующее объявление: «Брею тех и только тех жителей села, кто не бреется сам». Спрашивается, кто бреет брадобрея? Этот парадокс свидетельствует о том, что широко используемая теория множеств в ее интуитивном, «наивном» изложении является противоречивой. Формализация теории множеств, связанная, в частности, с устранением парадоксов, способствовала развитию не только методов теории множеств, но и такой науки, как математическая логика. Определение 1.2. Если все элементы множества А принадлежат также множеству В, причем
Определение 1.3. Если каждый элемент множества А есть элемент множества В, причем возможно
Множество, не содержащее элементов, называется пустым, и обозначается символом Ø. Пустое множество есть подмножество любого множества. Множества бывают конечные и бесконечные. Конечные множества содержат конечное число элементов. Множества, не являющиеся конечными, называются бесконечными. Число элементов конечного множества называется его мощностью. Мощность множества Пример 1.6. Дано множество
Множество всех подмножеств множества Пример 1.7. Дано множество
Операции над множествами Рассмотрим методы получения новых множеств их уже существующих. Определение 1.4. Пересечением множеств А и В называется множество С, состоящее из всех элементов, одновременно входящих и в множество А, и во множество В. Это записывается следующим образом:
Пример 1.7. Если множество А есть интервал (1; 5) а множество В есть интервал (2; 7), то пересечение множеств А и В есть интервал (2; 5): Определение 1.5. Объединением множеств А и В называется множество С, состоящее из всех элементов, каждый из которых принадлежит хотя бы одному из данных множеств или А, или В, или А и В одновременно. Это обозначается следующим образом:
Пример 1.8. Если множество А есть отрезок [1; 3] а множество В есть отрезок [2; 5], то объединение множеств А и В есть отрезок [1; 5]: Определение 1.6. Дополнением множества А называется множество всех элементов универсального множества U, каждый из которых не принадлежит множеству А. Дополнение множества А будем обозначать через
Пример 1.9. Если множество А есть отрезок [1; 3], то множество Определение 1.7. Разностью множеств А и В называется множество С, состоящее из всех элементов, принадлежащих множеству А, но не принадлежащих В:
Пример 1.10. Если множество А есть отрезок
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 583; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.74.54 (0.136 с.) |

 и
и 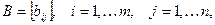 можно складывать. Суммой матриц A и B называют матрицу C того же размера, элементы которой равны сумме соответствующих элементов матриц А и В:
можно складывать. Суммой матриц A и B называют матрицу C того же размера, элементы которой равны сумме соответствующих элементов матриц А и В:
 (переместительный закон);
(переместительный закон);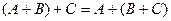 (сочетательный закон);
(сочетательный закон); .
.

 . Операция умножения матрицы на число осуществляется по правилу:
. Операция умножения матрицы на число осуществляется по правилу: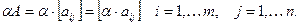
 ;
; ;
;

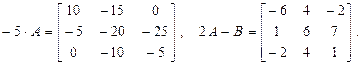
 называется матрица
называется матрица  , каждый элемент которой определяется выражением:
, каждый элемент которой определяется выражением:
 и
и  , то
, то

 Рис 1. 1 Схема вычисления элемента
Рис 1. 1 Схема вычисления элемента
 и ВА.
и ВА.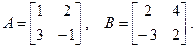


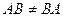 .
. (сочетательный закон);
(сочетательный закон); (распределительный закон).
(распределительный закон). .
. ;
; ;
;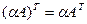 ;
; .
.
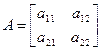
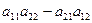 :
:
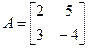


 .
.
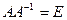






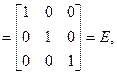
 откуда
откуда  Итак, способ построения обратной матрицы получен:
Итак, способ построения обратной матрицы получен: .
.






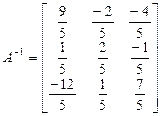


 :
:

 :
: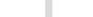

 :
:
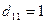 на его алгебраическое дополнение:
на его алгебраическое дополнение:



 .
.



 .
. .
.

 имеет ненулевой минор порядка
имеет ненулевой минор порядка  .Тогда можно рассматривать только миноры порядка
.Тогда можно рассматривать только миноры порядка  , которые содержат упомянутый ненулевой минор порядка
, которые содержат упомянутый ненулевой минор порядка  .
.








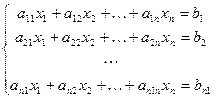
 , для которой
, для которой 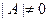 . Запишем матричное равенство (5.10) в следующем виде:
. Запишем матричное равенство (5.10) в следующем виде:


 заменой соответствующего номеру неизвестного столбца столбцом свободных членов данной системы уравнений (4.1). Обозначим их следующим образом:
заменой соответствующего номеру неизвестного столбца столбцом свободных членов данной системы уравнений (4.1). Обозначим их следующим образом:





 (пример 4.1).
(пример 4.1).







 обозначается отношение принадлежности. Запись
обозначается отношение принадлежности. Запись  означает, что элемент
означает, что элемент  является элементом множества
является элементом множества  .
. и
и  считаются равными, если они состоят из одних и тех же элементов.
считаются равными, если они состоят из одних и тех же элементов.

 ,
, 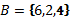 и
и  . В силу того, что все три множества состоят из одних и тех же элементов, справедлива запись
. В силу того, что все три множества состоят из одних и тех же элементов, справедлива запись  .
. и
и  . Эти множества нельзя считать равными, так как единственным элементом множества
. Эти множества нельзя считать равными, так как единственным элементом множества 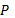 есть множество
есть множество  , множество
, множество  состоит из двух элементов: чисел 1 и 2.
состоит из двух элементов: чисел 1 и 2.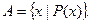
 содержит один элемент:
содержит один элемент:  состоит из набора элементов
состоит из набора элементов 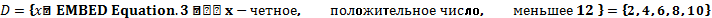 .
.


 , и
, и  . Для этих множеств справедливо
. Для этих множеств справедливо  , поскольку множество
, поскольку множество  включает множество
включает множество 
 .
. . Тогда
. Тогда  . Если множество
. Если множество  элементов, то множество
элементов, то множество  . Множество-степень содержит следующие подмножества:
. Множество-степень содержит следующие подмножества:

 (коммутативность);
2.
(коммутативность);
2.  (ассоциативность);
3.
(ассоциативность);
3.  ;
4.
;
4.  ;
5.
;
5.  Ø = Ø.
Ø = Ø.

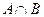
 .
.
 (коммутативность);
2.
(коммутативность);
2.  (ассоциативность);
3.
(ассоциативность);
3.  (дистрибутивность);
4.
(дистрибутивность);
4.  ;
5.
;
5.  ;
6.
;
6.  Ø = Ø.
Ø = Ø.


 .
.
 ;
2.
;
2. 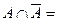 Ø
3.
Ø
3. 

 .
. .
.
 .
Из определения разности множеств следует, что имеет место равенство
.
Из определения разности множеств следует, что имеет место равенство  .
.


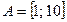 , а множество В есть отрезок
, а множество В есть отрезок  , то разность
, то разность  представляет собой полуинтервал
представляет собой полуинтервал  , а
, а  полуинтервал
полуинтервал  .
.


