
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Случайные события. Частота. Вероятность.Стр 1 из 5Следующая ⇒
ОСНОВНЫЕ ПОНЯТИЯ Случайные события. Частота. Вероятность. Теория вероятностей — математическая наука, изучающая закономерности массовых случайных явлений (событий). Случайным событием (или просто событием) называется всякое явление, которое может произойти или не произойти при осуществлении определенной совокупности условий. Теория вероятностей имеет дело с такими событиями, которые имеют массовый характер. Это значит, что данная совокупность условий может быть воспроизведена неограниченное число раз. Каждое такое осуществление данной совокупности условий называют испытанием (или опытом). Если, например, испытание состоит в бросании монеты, то выпадение герба является событием; если испытание — изготовление подшипника данного типа, то соответствие подшипника стандарту — событие; если испытание — бросание игральной кости, т. е. кубика, на гранях которого проставлены цифры (очки) от 1 до 6, to выпадение пятерки — событие. События будем обозначать заглавными буквами латинского алфавита: A, В, С,.... Пусть при n испытаниях событие A появилось m раз. Отношение m/n называется частотой (относительной частотой) события A и обозначается Р*(А)=m/n Опыт показывает, что при многократном повторении испытаний частота Р*(А) случайного события обладает устойчивостью. Поясним это на примере. Пусть при бросании монеты 4040 раз герб выпал 2048 раз. Частота появления герба в данной серии опытов равна Р*(А)=m/n=2048/4040=0,5069. При бросании той же монеты 12000 раз герб выпал 6019 раз. Следовательно, в этом случае частота Р*(А)=6019/12000=0,5016. Наконец, при 24000 бросаний герб появился 12012 раз с частотой Р*(А)=0,5005. Таким образом, мы видим, что при большом числе бросаний монеты частота появления герба обладает устойчивостью, т. е. мало отличается от числа 0,5. Как показывает опыт, это отклонение частоты от числа 0,5 уменьшается с увеличением числа испытаний. Наблюдаемое в этом примере свойство устойчивости частоты является общим свойством массовых случайных событий, а именно, всегда существует такое число, к которому приближается частота появления данного события, мало отличаясь от него при большом числе испытаний. Это число называется вероятностью события. Оно выражает объективную возможность появления события. Чем больше вероятность события, тем более возможным оказывается его появление. Вероятность события A будем обозначать через Р(А). В рассмотренном выше примере вероятность появления герба, очевидно, равна 0,5.
Событие называется достоверным, если оно в данном опыте обязательно должно произойти; наоборот, событие называется невозможным, если оно в данном опыте не может произойти. Пусть, например, из урны, содержащей только черные шары, вынимают шар. Тогда появление черного шара — достоверное событие; появление белого шара — невозможное событие. Если событие достоверно, то оно произойдет при каждом испытании (m=n). Поэтому частота достоверного события всегда равна единице. Наоборот, если событие невозможно, то оно ни при одном испытании не осуществится (m=0). Следовательно, частота невозможного события в любой серии испытаний равна нулю. Поэтому вероятность достоверного события равна единице, а вероятность невозможного события равна нулю. Если событие A не является ни достоверным, ни невозможным, то его частота m/n при большом числе испытаний будет мало отличаться от некоторого числа p (где 0 < p < 1) — вероятности события A. Совмещением (или произведением) двух событий A и В называется событие, состоящее в совместном наступлении как события A, так и события В. Это событие будем обозначать АВ или ВА. Аналогично, совмещением нескольких событий, например A, В и С, называется событие D=ABC, состоящее в совместном наступлении событий A, В и С. Объединением (или суммой) двух событий A и В называется событие С, заключающееся в том, что произойдет по крайней мере одно из событий A или В. Это событие обозначается так: С=А+В. Объединением нескольких событий называется событие, состоящее в появлении по крайней мере одного из них. Запись D=A+B+C означает, что событие D есть объединение событий A, В и С. Два события A и В называются несовместными, если наступление события A исключает наступление события В. Отсюда следует, что если события A и В несовместны, то событие AB — невозможное.
Аксиомы вероятностей. Пусть A и B — два несовместных события, причем в n испытаниях событие A произошло m1 раз, а событие В произошло m2 раз. Тогда частоты событий A и В соответственно равны P*(A)=m1/n, P*(B)=m2/n. Так как события A и В несовместны, то событие A+B в данной серии опытов произошло m1+m2 раз. Следовательно,
Таким образом, частота события A+B равна сумме частот событий A и В. Но при больших n частоты P*(A), P*(B) и P*(A+B) мало отличаются от соответствующих вероятностей P(A), P(B) и P(A+B). Поэтому естественно принять, что если A и В — несовместные события, то P(A+B)=P(A)+P(B) Изложенное позволяет высказать следующие свойства вероятностей, которые мы принимаем в качестве аксиом. Аксиома 1. Каждому случайному событию A соответствует определенное число Р(А), называемое его вероятностью и удовлетворяющее условию Аксиома 2. Вероятность достоверного события равна единице. Аксиома 3 (аксиома сложения вероятностей). Пусть A и В — несовместные события. Тогда вероятность того, что произойдет хотя бы одно из этих двух событий, равна сумме их вероятностей:
Аксиома 3 допускает обобщение на случай нескольких событий, а именно: если события A1, A2,..., An, попарно несовместны, то
Событием, противоположным событию Пусть, например, событие Теорема 1. Для любого события
Доказательство. Событие Теорема 2. Вероятность невозможного события равна нулю. Доказательство непосредственно следует из аксиомы 2 и теоремы 1, если заметить, что невозможное событие противоположно достоверному событию.
Формула полной вероятности. Пусть событие A может произойти только вместе с одним из попарно несовместных событий H1, H2,..., Hn, образующих полную группу. Тогда, если произошло событие A, то это значит, что произошло одно из попарно несовместных событий H1A, H2A,..., HnA. Следовательно,
Применяя аксиому сложения вероятностей, имеем
Но
Эта формула называется формулой полной вероятности. События H1, H2,..., Hn часто называют «гипотезами».
Пример. В магазин поступили электрические лампочки одного типа, изготовленные на четырех ламповых заводах: с 1-го завода 250 шт., со 2-го — 525 шт., с 3-го — 275 шт. и с 4-го — 950 шт. Вероятность того, что лампочка прогорит более 1500 часов, для 1-го завода равна 0,15, для 2-го — 0,30, для 3-го — 0,20, для 4-го — 0,10. При раскладке по полкам магазина лампочки были перемешаны. Какова вероятность того, что купленная лампочка прогорит более 1500 часов? Решение: Пусть A — событие, состоящее в том, что лампочка прогорит более 1500 часов, а Н1, Н2, Н3 и Н4 — гипотезы, что она изготовлена соответственно 1, 2, 3 или 4-м заводом. Так как всего лампочек 2000 шт., то вероятности гипотез соответственно равны
Далее, из условия задачи следует, что
Используя формулу полной вероятности (11), имеем
Формула Бейеса. Предположим, что производится некоторый опыт, причем об условиях его проведения можно высказать n единственно возможных и несовместных гипотез Спрашивается, как изменятся вероятности гипотез, если стало известным, что событие А произошло? Иными словами, нас интересуют значения вероятностей На основании соотношений (4) и (5) имеем
откуда
Но по формуле полной вероятности
Поэтому
Формула (12) называется формулой Бейеса*.
Пример. На склад поступило 1000 подшипников. Из них 200 изготовлены на 1-м заводе, 460—на 2-м и 340 - на 3-м. Вероятность того, что подшипник окажется нестандартным, для 1-го завода равна 0,03, для 2-го — 0,02, для 3-го — 0,01. Взятый наудачу подшипник оказался н естандартным. Какова вероятность того, что он изготовлен 1-м заводом? Решение: Пусть A — событие, состоящее в том, что взятый Подшипник нестандартный, а
Найдем
Таким образом, вероятность гипотезы, что подшипник изготовлен 1-м заводом, изменилась после того, как стало известно, что он нестандартен.
Таблица I.
Пример 3. Игральную кость бросают 80 раз. Определить вероятность того, что цифра 3 появится 20 раз. Решение: Здесь далее находим
СЛУЧАЙНЫЕ ВЕЛИЧИНЫ Понятие случайной величины является основным в теории вероятностей и ее приложениях. Случайными величинами, например, являются число выпавших очков при однократном бросании игральной кости, число распавшихся атомов радия за данный промежуток времени, число вызовов на телефонной станции за некоторый промежуток времени, отклонение от номинала некоторого размера детали при правильно налаженном технологическом процессе и т. д. Равномерное распределение. Пусть сегмент [a,b] оси Ox есть шкала некоторого прибора. Допустим, что вероятность попадания указателя в некоторый отрезок шкалы пропорциональна длине этого отрезка и не зависит от места отрезка на шкале. Отметка указателя прибора есть случайная величина
где k - коэффициент пропорциональности, не зависящий от x1 и x2, а разность x2-x1, - длина сегмента [x1,x2]. Так как при x1=a и x2=b имеем
Теперь легко найти функцию F(x) распределения вероятностей случайной величины
Так как
Наконец, если x>b, то F(x)=1, так как значения
График функции F(x) представлен на рис. 9. Плотность распределения вероятностей найдем по формуле (25). Если x<a или x>b, то
Таким образом,
График функции
Величина, плотность распределения которой задана формулой (27), называется равномерно распределенной случайной величиной
Нормальное распределение. Говорят, что случайная величина
График функции Ф(х) изображен на рис. 12.
Таким образом, если случайная величина
Пример 2. В каких пределах должна изменяться случайная величина, подчиняющаяся нормальному закону распределения, чтобы Из последнего примера следует, что если случайная величина подчиняется нормальному закону распределения, то можно утверждать с вероятностью, равной 0,9973, что случайная величина находится в интервале
Пример 2. В каких пределах должна изменяться случайная величина, подчиняющаяся нормальному закону распределения, чтобы Решение: По формуле (33) имеем
Следовательно,
Таблица II.
ЗАКОНЫ БОЛЬШИХ ЧИСЕЛ. Леммы Чебышева. В этом пункте докажем следующие две леммы, принадлежащие Чебышеву* Лемма 1. Пусть
Лемма 2. Пусть
ОСНОВНЫЕ ПОНЯТИЯ Случайные события. Частота. Вероятность. Теория вероятностей — математическая наука, изучающая закономерности массовых случайных явлений (событий). Случайным событием (или просто событием) называется всякое явление, которое может произойти или не произойти при осуществлении определенной совокупности условий. Теория вероятностей имеет дело с такими событиями, которые имеют массовый характер. Это значит, что данная совокупность условий может быть воспроизведена неограниченное число раз. Каждое такое осуществление данной совокупности условий называют испытанием (или опытом). Если, например, испытание состоит в бросании монеты, то выпадение герба является событием; если испытание — изготовление подшипника данного типа, то соответствие подшипника стандарту — событие; если испытание — бросание игральной кости, т. е. кубика, на гранях которого проставлены цифры (очки) от 1 до 6, to выпадение пятерки — событие. События будем обозначать заглавными буквами латинского алфавита: A, В, С,.... Пусть при n испытаниях событие A появилось m раз. Отношение m/n называется частотой (относительной частотой) события A и обозначается Р*(А)=m/n Опыт показывает, что при многократном повторении испытаний частота Р*(А) случайного события обладает устойчивостью. Поясним это на примере. Пусть при бросании монеты 4040 раз герб выпал 2048 раз. Частота появления герба в данной серии опытов равна Р*(А)=m/n=2048/4040=0,5069. При бросании той же монеты 12000 раз герб выпал 6019 раз. Следовательно, в этом случае частота Р*(А)=6019/12000=0,5016. Наконец, при 24000 бросаний герб появился 12012 раз с частотой Р*(А)=0,5005. Таким образом, мы видим, что при большом числе бросаний монеты частота появления герба обладает устойчивостью, т. е. мало отличается от числа 0,5. Как показывает опыт, это отклонение частоты от числа 0,5 уменьшается с увеличением числа испытаний. Наблюдаемое в этом примере свойство устойчивости частоты является общим свойством массовых случайных событий, а именно, всегда существует такое число, к которому приближается частота появления данного события, мало отличаясь от него при большом числе испытаний. Это число называется вероятностью события. Оно выражает объективную возможность появления события. Чем больше вероятность события, тем более возможным оказывается его появление. Вероятность события A будем обозначать через Р(А). В рассмотренном выше примере вероятность появления герба, очевидно, равна 0,5. Событие называется достоверным, если оно в данном опыте обязательно должно произойти; наоборот, событие называется невозможным, если оно в данном опыте не может произойти. Пусть, например, из урны, содержащей только черные шары, вынимают шар. Тогда появление черного шара — достоверное событие; появление белого шара — невозможное событие. Если событие достоверно, то оно произойдет при каждом испытании (m=n). Поэтому частота достоверного события всегда равна единице. Наоборот, если событие невозможно, то оно ни при одном испытании не осуществится (m=0). Следовательно, частота невозможного события в любой серии испытаний равна нулю. Поэтому вероятность достоверного события равна единице, а вероятность невозможного события равна нулю. Если событие A не является ни достоверным, ни невозможным, то его частота m/n при большом числе испытаний будет мало отличаться от некоторого числа p (где 0 < p < 1) — вероятности события A. Совмещением (или произведением) двух событий A и В называется событие, состоящее в совместном наступлении как события A, так и события В. Это событие будем обозначать АВ или ВА. Аналогично, совмещением нескольких событий, например A, В и С, называется событие D=ABC, состоящее в совместном наступлении событий A, В и С. Объединением (или суммой) двух событий A и В называется событие С, заключающееся в том, что произойдет по крайней мере одно из событий A или В. Это событие обозначается так: С=А+В. Объединением нескольких событий называется событие, состоящее в появлении по крайней мере одного из них. Запись D=A+B+C означает, что событие D есть объединение событий A, В и С. Два события A и В называются несовместными, если наступление события A исключает наступление события В. Отсюда следует, что если события A и В несовместны, то событие AB — невозможное.
Аксиомы вероятностей. Пусть A и B — два несовместных события, причем в n испытаниях событие A произошло m1 раз, а событие В произошло m2 раз. Тогда частоты событий A и В соответственно равны P*(A)=m1/n, P*(B)=m2/n. Так как события A и В несовместны, то событие A+B в данной серии опытов произошло m1+m2 раз. Следовательно,
Таким образом, частота события A+B равна сумме частот событий A и В. Но при больших n частоты P*(A), P*(B) и P*(A+B) мало отличаются от соответствующих вероятностей P(A), P(B) и P(A+B). Поэтому естественно принять, что если A и В — несовместные события, то P(A+B)=P(A)+P(B) Изложенное позволяет высказать следующие свойства вероятностей, которые мы принимаем в качестве аксиом. Аксиома 1. Каждому случайному событию A соответствует определенное число Р(А), называемое его вероятностью и удовлетворяющее условию Аксиома 2. Вероятность достоверного события равна единице.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 260; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.221.53.209 (0.244 с.) |

 .
.
 , называется событие
, называется событие  , состоящее в ненаступлении события
, состоящее в ненаступлении события 


 (i=1, 2,..., n), поэтому
(i=1, 2,..., n), поэтому



 , имеющих вероятности
, имеющих вероятности 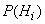 . Пусть в результате опыта может произойти или не произойти событие А, причем известно, что если опыт происходит при выполнении гипотезы
. Пусть в результате опыта может произойти или не произойти событие А, причем известно, что если опыт происходит при выполнении гипотезы  , то
, то 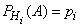

 .
.



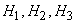 - гипотезы, что он изготовлен соответственно 1-м, 2-м или 3-м заводом. Вероятности указанных гипотез составляют
- гипотезы, что он изготовлен соответственно 1-м, 2-м или 3-м заводом. Вероятности указанных гипотез составляют

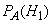 , т. е. вероятность того, что подшипник, оказавшийся нестандартным, изготовлен 1-м заводом. По формуле Бейеса имеем
, т. е. вероятность того, что подшипник, оказавшийся нестандартным, изготовлен 1-м заводом. По формуле Бейеса имеем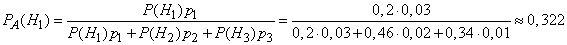
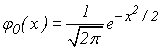




 могущая принять любое значение из сегмента [a,b]. Поэтому
могущая принять любое значение из сегмента [a,b]. Поэтому  . Если, далее, x1 и x2 (x1<x2) - две любые отметки на шкале, то согласно условию имеем
. Если, далее, x1 и x2 (x1<x2) - две любые отметки на шкале, то согласно условию имеем

 , то
, то  так как
так как  . По аксиоме сложения вероятностей
. По аксиоме сложения вероятностей  . Согласно формуле (26), в которой принимаем x1=a, x2=х имеем
. Согласно формуле (26), в которой принимаем x1=a, x2=х имеем
 , то при
, то при 


 . Если a<x<b, то
. Если a<x<b, то


 изображен на рис. 10. Заметим, что в точках a и b функция
изображен на рис. 10. Заметим, что в точках a и b функция 
 нормально распределена или подчиняется закону распределения Гаусса, если ее плотность распределения
нормально распределена или подчиняется закону распределения Гаусса, если ее плотность распределения 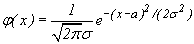
 >0. Смысл параметров a и
>0. Смысл параметров a и 
 и
и  . При
. При  график функции асимптотически приближается к оси Ox. Можно показать, что при увеличении
график функции асимптотически приближается к оси Ox. Можно показать, что при увеличении 

 . Тогда
. Тогда




 . По формуле (23) имеем
. По формуле (23) имеем
 ,
, 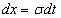 и
и
 не берется в элементарных функциях. Поэтому для вычисления определенного интеграла (30) вводится функция
не берется в элементарных функциях. Поэтому для вычисления определенного интеграла (30) вводится функция



 ; при
; при  величина
величина  практически равна 1/2 (см. табл. II).
практически равна 1/2 (см. табл. II). 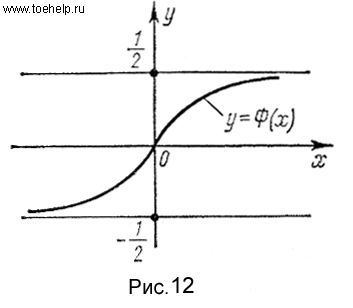
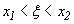 , определяется соотношением (32).
, определяется соотношением (32). 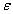 , т.е.
, т.е.  .
.  равносильно неравенствам
равносильно неравенствам  , то полагая в соотношении (32)
, то полагая в соотношении (32)  ,
, 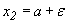 получим
получим

 ;
; 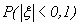 ;
; (Решение)
(Решение) . Так как данная вероятность близка к единице, то можно считать, что значения нормально распределенной случайной величины практически не выходят за границы интервала
. Так как данная вероятность близка к единице, то можно считать, что значения нормально распределенной случайной величины практически не выходят за границы интервала 
 . Из табл. II находим, что этому значению
. Из табл. II находим, что этому значению  соответствует
соответствует  , откуда
, откуда 

 — случайная величина, принимающая только неотрицательные значения; тогда
— случайная величина, принимающая только неотрицательные значения; тогда 
 — случайная величина, а
— случайная величина, а  - положительное число. Тогда вероятность того, что модуль отклонения случайной величины.
- положительное число. Тогда вероятность того, что модуль отклонения случайной величины. 



