
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Занятие 8. Дискретные и непрерывные случайные величины.
Краткая теоретическая часть а) Ряд, многоугольник и функция распределения случайной дискретной величины Случайная величина называется дискретной, если ее частные (возможные) значения можно пронумеровать. Дискретная случайная величина Х может быть задана рядом распределения или функцией распределения (интегральным законом распределения). Рядом распределения называется совокупность всех возможных значений xi, и соответствующих им вероятностей pi = P(X = xi). Ряд распределения может быть задан в виде таблицы (табл. 1) или формулой. Таблица 1.
Вероятности pi удовлетворяют условию
где число возможных значений n может быть конечным или бесконечным. Графическое изображение ряда распределения называется многоугольником распределения. Для его построения возможные значения случайной величины (xi) откладываются по оси абсцисс, а вероятности pi - по оси ординат; точки Ai с координатами (xi; pi) соединяются ломаными линиями (рис. 1).
где суммирование ведется по всем значениям i, для которых xi<x. б) Функция распределения и плотность вероятности непрерывной случайной величины Случайная величина называется непрерывной, если существует неотрицательная функция f (x), удовлетворяющая при любых x равенству
Функция f (x) называется плотностью вероятности
Непрерывная случайная величина задается либо функцией распределения F (x) (интегральным законом распределения), либо плотностью вероятности f (x) (дифференциальным законом распределения). Функция распределения F (x) = Р(X < x), где x — произвольное действительное число, дает вероятность того, что случайная величина Х окажется меньше x. Функция распределения F (x) имеет следующие основные свойства:
Плотность вероятности (дифференциальный закон распределения) f (x) обладает следующими основными свойствами:
Величина xp, определяемая равенством F(xp) = p, называется квантилем порядка p, квантиль x0,5 называют медианой. Если плотность имеет максимум, то значение x, при котором f (x)достигает максимума, называется модой.
Тест Дискретные и непрерывные случайные величины.
1. Какое из данных утверждений не является определением случайной величины? а) Случайной величиной б) Функция в) г) Функция
2. Какое из следующих утверждений является определением функции распределения случайной величины? а) Вероятность б) Вероятность в) Вероятность
3. Знание функции распределения случайной величины полностью с вероятностной точки зрения характеризует случайную величину. А что она определяет? а) Функция распределения случайной величины б) Функция распределения случайной величины в) Функция распределения случайной величины 4. Плотность распределения – это понятие, применимое: а) только к дискретным случайным величинам б) только к непрерывным случайным величинам в) ко всем случайным величинам
5. Выберите те из следующих выражений, которые являются свойствами функции распределения случайной величины
а) б) в) г) д) е) ж) з)
6. Укажите те из следующих утверждений, которые не являются свойствами плотности распределения а) б) в) г) д) е) ж) Решение типовых задач
а) Ряд, многоугольник и функция распределения случайной дискретной величины Пример 8.1. Из партии, содержащей 100 изделий, среди которых имеется 10 дефектных, выбраны случайным образом пять изделий для проверки их качества. Построить ряд распределений случайного числа Х дефектных изделий, содержащихся в выборке.
Решение. Введем в рассмотрение случайную величину X – число дефектных изделий среди выбранных пяти. Так как в выборке число дефектных изделий может быть любым целым числом в пределах от 0 до 5 включительно, то возможные значения xi, случайной величины Х равны: x1 = 0, x2 = 1, x3 = 2, x4 = 3, x5 = 4, x6 = 5. Вероятность Р(X = k) того, что в выборке окажется ровно k (k=0, 1, 2, 3, 4, 5) дефектных изделий, равна
В результате расчетов по данной формуле с точностью до 0,001 получим: p1 = P(X = 0)=0,583, p1 = P(X = 1)=0,340, p1 = P(X = 2)=0,070, p1 = P(X = 3)=0,007, p1 = P(X = 4)=0, p1 = P(X = 5)=0. Используя для проверки равенство Таблица 2
Пример 8.2. Изделия испытываются при перегрузочных режимах. Вероятности для каждого изделия пройти испытание равны 4/5 и независимы. Испытания заканчиваются после первого же изделия, не выдержавшего испытания. Вывести формулу для ряда распределения числа испытаний.
Решение. Введем в рассмотрение случайную величину X – число взятых изделий для испытаний. Испытания заканчиваются на k- м изделии (k = 1, 2, 3,...), если первые k —1 изделий пройдут испытания, a k - e изделие не выдержит испытания. Если Х — случайное число испытаний, то
Полученная формула для ряда распределения эквивалентна таблице 3. Таблица 3.
Особенность данной задачи состоит в том, что теоретически число испытаний может быть бесконечно большим, однако вероятность такого события стремится к нулю:
Пример 8.3. На пути движения автомашины четыре светофора. Каждый из них с вероятностью 0,5 либо разрешает, либо запрещает автомашине дальнейшее движение.
Решение. Х — случайное число светофоров, пройденных автомашиной без остановки; оно может принимать следующие значения: x1 = 0, x2 = 1, x3 = 2, x4 = 3, x5 = 4,
где p — вероятность для светофора задержать автомашину (p = 0,5). В результате вычислений получим p1 = 0,5, p2 = 0,25, p3 = 0,125, p4 = 0,0625, p5 = 0,0б25. По полученным данным строим многоугольник распределения вероятностей (рис. 2).
Пример 8.4. Космическая ракета имеет прибор, состоящий из четырех блоков a1, a2, a3 и a4, каждый из которых дает отказ при попадании в него хотя бы одной элементарной частицы. Отказ прибора в целом наступает как при отказе блока a1, так и при одновременном отказе всех трех блоков a2, a3 и a4. Построить функцию распределения F (x) случайного числа Х частиц, после попадания которых в прибор он дает отказ, если вероятность частице, попавшей в прибор, попасть в блок a1 равна p1 = 0,4, а в блоки a2, a3 и a4 соответственно равна p2 = p3 = p4 = 0,2.
Решение. Обозначим A1, A2, A3 и A4 события, состоящие в отказе блоков a1, a2, a3 и a4 с оответственно. Искомая функция распределения F (x) равна вероятности того, что при числе попаданий n<x прибор выйдет из строя, т. е. F (x) = P(A1 +A2A3A4) Используя формулу
где все вероятности определяются при условии попадания в прибор n (n >1) частиц. Так кaк p1 + p2 + p3 + p4 = 1 и при каждом попадании частицы в прибор обязательно дает отказ один и только один из блоков, то
Таким образом, учитывая, что p2 = p3 = p4 = 0,2, получим
где под [ x ] понимается наибольшее целое число, меньшее x, например [5,9] = 5, [5] = 4. При n
б) Функция распределения и плотность вероятности непрерывной случайной величины Пример 8.5. Проекция Х радиуса-вектора случайной точки окружности радиуса a на диаметр - имеет функцию распределения (закон арксинуса)
Определить: а) вероятность того, что Х окажется в пределах промежутка ( б) квантиль x0,75; в) плотность вероятности f (x) случайной величины X; г) моду и медиану распределения. Решение. а) Вероятность того, что Х окажется в пределах (
б) По условию p = 0,75; решая уравнение
находим
в) Плотность вероятности f (x) случайной величины Х равна: 1) для всех x, принадлежащих промежутку (- а, а),
2) нулю для всех остальных значений x. г) Закон арксинуса моды не имеет, так как функция
не имеет максимума. Решая уравнение
находим медиану x0,5 = 0.
Пример 8.6. Плотность вероятности случайной величины равна
Требуется: а) найти коэффициент а; 6) найти функцию распределения случайной величины X; в) вычислить вероятность попадания случайной величины в интервал Решение. а) Коэффициент а определяем с помощью равенства
Отсюда
Двукратным интегрированием по частям получаем
Следовательно,
б) Функция распределения F (x) случайной величины Х определяется по формуле
в) Вероятность
8.4. Задачи для самостоятельной работы а) Ряд, многоугольник и функция распределения случайной дискретной величины
8.1. Построить ряд распределения и функцию распределения случайного числа попаданий мячом в корзину при одном броске, если вероятность попадания мячом в корзину при одном броске p= 0,3. 8.2. Опыт состоит из трех независимых бросаний монеты, при каждом из которых герб выпадает с вероятностью p = 0,5. Для случайного числа появлений герба построить: а) ряд распределения; б) многоугольник распределения; в) функцию распределения.
8.3. Производятся последовательные независимые испытания пяти приборов на надежность. Каждый следующий прибор испытывается только в том случае, если предыдущий оказался надежным. Построить ряд распределения случайного числа испытанных приборов, если вероятность выдержать испытания для каждого из них равна 0,9.
8.4. Два баскетболиста поочередно забрасывают мяч в корзину до тех пор, пока один из них не попадет. Построить ряд распределения случайного числа бросков, производимых каждым из баскетболистов, если вероятность попадания для первого, равна 0,4, а для второго 0,6.
8.5. Сигналы на включение приборов подаются через каждые 5 сек. Время от момента передачи сигнала до включения прибора 16 сек. Подача сигналов прекращается сразу же после того, как включится хотя бы один прибор. Найти ряд распределения для случайного числа поданных сигналов, если вероятность включения для каждого прибора равна
8.6. Производятся испытания n изделий на надежность, причем вероятность выдержать испытания для каждого изделия равна р. Построить ряд распределения случайного числа изделий, выдержавших испытания.
8.7. Вероятность выпадения герба при каждом из пяти бросаний монеты равна 0,5. Составить ряд распределения отношения числа Х появлений герба к числу Y появлений решетки.
б) Функция распределения и плотность вероятности непрерывной случайной величины 8.8. Функция распределения равномерно распределенной случайной величины Х имеет вид
Найти плотность вероятности случайной величины X. 8.9. Дана функция распределения случайной величины (закон нормального распределения):
Найти плотность вероятности случайной величины X.
8.10. В книге Г. Крамера дана функция распределения годовых доходов лиц, облагаемых налогом:
Определить размер годового дохода, который для случайно выбранного налогоплательщика может быть превзойден с вероятностью 0,5.
8.11. Функция распределения случайного времени безотказной работы радиоаппаратуры имеет вид (экспоненциальный закон распределения)
Найти: а) вероятность безотказной работы аппаратуры в течение времени Т; б) плотность вероятности f (t).
8.12. Случайная величина эксцентриситета детали характеризуется функцией распределения Рэлея
Найти: а) плотность вероятности f(x); б) медиану распределения; в) моду распределения.
8.13. Функция распределения Вейбулла
в ряде случаев характеризует срок службы элементов электронной аппаратуры. Найти: а) плотность вероятности f(x);
б) квантиль распределения порядка p; в) моду распределения.
8.14. Дана функция распределения случайной величины X (закон Коши): F (х) = с + b arctg Определить: а) постоянные с и b; б) плотность вероятности; в) Р(
8.15. Каково должно быть а, чтобы
8.16. При каком значении а функция
является плотностью вероятности случайной величины X? Найти: а) функцию распределения случайной величины X; б) вероятность попадания случайной величины, в интервал (- 1, 1).
8.17. Азимутальный лимб имеет цену деления 1°. Какова вероятность при считывании азимутального угла сделать ошибку в пределах ± 10', если отсчет округляется до ближайшего целого числа градусов?
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 1592; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.172.146 (0.104 с.) |
 ,
, Функцией распределения (интегральным законом распределения) случайной величины Х называется функция F (x), равная вероятности P(X < x) того, что случайная величина будет меньше произвольно выбранного значения x. Функция F (x) вычисляется по формуле
Функцией распределения (интегральным законом распределения) случайной величины Х называется функция F (x), равная вероятности P(X < x) того, что случайная величина будет меньше произвольно выбранного значения x. Функция F (x) вычисляется по формуле ,
, .
.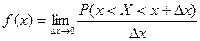 .
.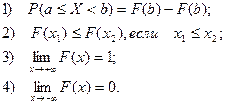
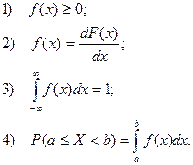
 называется вещественная функция, определенная на элементах пространства элементарных исходов
называется вещественная функция, определенная на элементах пространства элементарных исходов  таким образом, что для любого числа
таким образом, что для любого числа  , принадлежащего вещественной прямой, множество
, принадлежащего вещественной прямой, множество  , на котором функция
, на котором функция  , является элементом поля событий
, является элементом поля событий  , то есть
, то есть 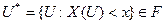
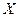 является случайной величиной, если для него определена вероятность
является случайной величиной, если для него определена вероятность 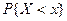

 является некоторой функцией аргумента
является некоторой функцией аргумента  определяет вероятность того, что случайная величина
определяет вероятность того, что случайная величина 

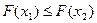 , если
, если 

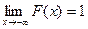

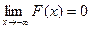



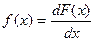

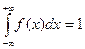


 .
. , убеждаемся, что расчеты и округление произведены правильно (см. табл. 2).
, убеждаемся, что расчеты и округление произведены правильно (см. табл. 2).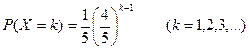
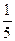


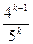
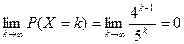
 Вероятности pi = P(X = xi) того, что число пройденных светофоров Х будет равно данному частному значению, вычисляются по формуле
Вероятности pi = P(X = xi) того, что число пройденных светофоров Х будет равно данному частному значению, вычисляются по формуле
 и применяя формулу сложения вероятностей, получим
и применяя формулу сложения вероятностей, получим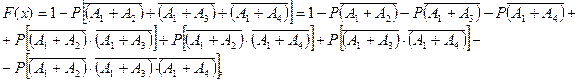

 ,
,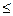 1 F (x) = 0.
1 F (x) = 0. Таким образом, график функции распределения вероятностей для нескольких начальных значений x имеет вид, представленный на рис. 3.
Таким образом, график функции распределения вероятностей для нескольких начальных значений x имеет вид, представленный на рис. 3.
 );
); .
. ,
, .
. ,
,
 ,
,
 .
. .
.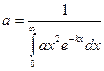 .
. .
. и плотность вероятности имеет вид
и плотность вероятности имеет вид .
. .
. попадания случайной величины Х в заданный промежуток вычисляется по формуле
попадания случайной величины Х в заданный промежуток вычисляется по формуле .
. .
. .
. .
. .
. .
. .
.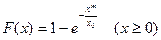
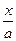 .
. ).
). являлось плотностью вероятности случайной величины X, изменяющейся в бесконечных пределах?
являлось плотностью вероятности случайной величины X, изменяющейся в бесконечных пределах?




