
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Некоторые исторические сведения о возникновенииСтр 1 из 7Следующая ⇒
Лекция 1. Некоторые исторические сведения о возникновении И развитии теории вероятностей. Теория вероятностей Требования со стороны естествознания и общественной практики (теория ошибок наблюдений, задачи теории стрельбы, проблемы статистики) привели к необходимости дальнейшего развития теории вероятностей и привлечения аналитического аппарата. Особенно значительную роль в развитии аналитических методов сыграли Муавр (1667-1754), Лаплас (1749-1827), Гаусс (1777-1855), Пуассон(1781-1840). С середины XIX столетия и приблизительно до двадцатых годов ХХ столетия развитие теории вероятностей связано в значительной мере с именами русских ученых - Чебышева П.Л(1821-1894), Маркова А.А. (1856-1922), Ляпунова А.М. (1856-1918).Этот успех русской науки был подготовлен деятельностью Буняковского В.Я. (1804-1889), широко использовавшего исследования по применению теории вероятностей в статистике, в особенности в страховом деле и демографии. Современное развитие теории вероятностей характеризуется всеобщим подъемом интереса к ней, а также расширением круга ее практических приложений. Одной из важнейших сфер приложения теории вероятностей является экономика. Многие экономические показатели (производительность труда, заработная плата, выработка на одного рабочего за смену,, страховой запас, резервные мощности, государственные резервы, спрос на товары производителя и др.) являются случайными величинами. Прогнозирование экономических явлений осуществляется на основе эконометрического моделирования,, регрессионного анализа, трендовых и сглаживающих моделей, опирающихся на теорию вероятностей. Результаты теории вероятностей используются для организации производства (статистический контроль в производстве). Большое значение имеет разработка статистических методов управления качеством продукции в процессе производства. Для инженерного дела серьезную роль приобрела теория надежности, широко использующая методы теории вероятностей.
Мы определили в самом начале теорию вероятностей как науку, изучающую случайные явления. Какой смысл вкладывается в понятие «случайное явление» мы рассмотрим несколько позже, а сейчас ограничимся некоторыми замечаниями. В обыденных представлениях, житейской практике считается, что случайные события представляют собой нечто крайне редкое, идущее вразрез установившемуся порядку вещей, закономерному развитию событий. Случайные события, как они понимаются в теории вероятностей, обладают рядом характерных особенностей; в частности, все они происходят в массовых явлениях, способных многократно повторяться при воспроизведении определенного комплекса условий. Теория вероятностей не занимается изучением уникальных событий, которые не допускают повторений.
Лекция 2. Определение случайного события. Элементарные исходы эксперимента - это простейшие случайные события и определению не подлежат. Однако в каждом случайном эксперименте кроме элементарных могут происходить и другие случайные события. Так, например, в примере 2 можно рассмотреть события: А - хотя бы один раз появится герб, В - герб появится при первом бросании, С - хотя бы один раз появится решка и т. А - выпадение четного числа очков, В - выпадение числа очков, не меньше 4, С – выпадение нечетного числа очков и т. д. Событие А произойдет, если будет иметь место один из исходов эксперимента ГГ,ГР,РГ.: выпадет число очков, равное 2 или 4 или 6. Таким образом,
А = Пусть в примере 3 В примере 3 могут произойти события: А - хотя бы один раз выпадет герб, В - герб выпадет при первом бросании, С - хотя бы один раз выпадет решка и т.д. Здесь А={ ГГ, ГР, РГ }, В={ ГГ,ГР }, С = { РР,РГ,ГР }. Пусть в примере 4 событие А состоит в том, что будет сделано не более трех бросаний. Тогда А = Рассмотрим задачу о встрече (пример 4).Предположим, что каждое из лиц А и В ожидает другого время, не большее чем t, С ={(x, y): (Рис.2).
Рис.2
Итак, случайное событие А – это некоторое подмножество Алгебра событий. Событие называется невозможным, если оно в эксперименте заведомо не наступит и обозначается Если в случайном эксперименте из наступления события А следует наступление события В, то говорят, что А влечет В Если А Суммой двух событий А и В называют событие А + В (А
Рис.3 В примере 2 А + В= { 2, 4, 5, 6 }. Аналогичный смысл имеет сумма любого числа событий. Если I -произвольное множество значений некоторого индекса i, A Произведением двух событий А и B называют событие AВ (А дящее тогда и только тогда, когда происходит и событие А, и событие В (все события А Произведение событий соответствует пересечению множеств, (Рис.4).
Рис.4 Для событий из примера 2 АВ = { 4, 6 }. Разностью А \ В двух событий А и В есть событие, происходящее тогда и только тогда. когда происходит А, но не происходит В. Разность событий соответствует разности множеств, (Рис.5)
Рис.5. В примере 2 А \ В = { 2 }. Событие
Рис.6. В примере 2 Операции сложения и умножения событий обладают следующими свойствами: а) А+В = В+А, АВ = ВА (коммутативность); б) (А+В)+С=А+(В+С ), А(ВС)=(АВ)С (ассоциативность); в) (А+В)С=АС+ВС) (дистрибутивность умножения относительно cложения). Отметим еще некоторые очевидные соотношения: А Два события А и В называются несовместными, если невозможно их совместное наступление, иными словами АВ = Совокупность событий А 1) хотя бы одно из этих событий непременно происходит;
2) любая пара событий несовместна, А Лекция 3. Классическое определение вероятности.
Вероятность – это количественная оценка возможности наступления случайного события. По классическому определению, вероятностью случайного события Р(А) называется отношение числа m благоприятствующих исходов к общему числу n равновозможных исходов эксперимента Р(А) = Классическая вероятность обладает следующими свойствами: 1. Р(А) 2. Вероятность достоверного события Р( 3. Если событие С = А+В, причем А и В несовместны, то Р(С) = Р(А)+Р(В). 4. Вероятность противоположного события Р( 5. Вероятность невозможного события равна нулю Р( 6. Если А 7. Вероятность любого события заключена между нулем и единицей 0 Рассмотрим примеры на вычисление вероятностей. Пример 1. Один раз подбрасывают монету. Чему равна вероятность выпадения герба? Здесь Пример 2. Один раз подбрасывают шестигранный игральный кубик. Чему равна вероятность того, что выпадет число очков, не менее четырех?
В более сложных задачах не представляется возможным наглядно записать все исходы эксперимента, а также благоприятные случайному событию исходы. В таких случаях применяются комбинаторные методы подсчета чисел m и n. Пример 3. В ящике находится 10 деталей, среди которых 3 бракованных. Из ящика наугад извлекают 5 деталей. Найти вероятность того, что среди них окажется две бракованных. Событие А - среди 5-ти извлеченных деталей 2 бракованных, а три доброкачественных. Для подсчета m и n используем правило сочетаний: n = Отметим недостатки классического определения вероятностей: 1.Классическое определение невозможно применить в случае бесконечного пространства элементарных исходов. 2.Существует проблема нахождения разумного способа выделения «равновозможных случаев». Например, как определить вероятность того, что родившийся ребенок окажется мальчиком? По мере развития теории вероятностей появлялись другие определения вероятности, которые устраняли недостатки классического. Эти определения будут рассмотрены немного позже.
Случайные величины. Функция распределения. Функцией распределения F(x) называется вероятность того, что случайная величина x примет значение меньше x, где x– любое действительное число,
F(x) = р (x < х), где - ¥ < х < ¥ Свойства функции распределения: 1. 0 £ F(x) £ 1 2. При х 3. При х 4. Вероятность попадания случайной величины в произвольный интервал действительной оси [x
Докажем это свойство. Для этого рассмотрим событие (x < х2). Очевидно, что это событие можно записать в виде суммы: (x < х2) = (х1 £ x < х2) + (x < х1), используя формулу сложения для несовместных событий, получим р(x < х2) = р(х1 £ x < х2) + р(x < х1), откуда следует F (х2) = р(х1 £ x < х2) + F (х1) или р(х1 £ x < х2) = F (х2)- F (х1). 5. Функция распределения F (х) – неубывающая функция на всей оси Ох, т.е. если х2 > х1, то F (х2) ³ F (х1). Действительно, пусть х2 > х1 , в пункте 5 показано, что для F (х2) справедливо равенство F (х2) = р(х1 £ x < х2) + F (х1), а так как р(х1 £ x < х2) что F (х2) ³ F (х1). 6. Функция распределения непрерывна слева
Зная закон распределения дискретной случайной величины, можно вычислить функцию распределения по формуле F (x) = где суммирование распространяется на все те значения индекса i, для которых
Пример 12. Построить функцию распределения для случайной величины, рассмотренной в Примере 11. Поскольку функция F(x) определена для всей действительных значений x, то рассмотрим последовательно интервалы: 1. х Î (- ∞; 0], F (x) = р(x < x) = 0, так как событие (x < x) на данном интервале является невозможным событием. 2. х Î (0; 1], F (x) = р(x = 0) = 1/4, здесь неравенству x < x удовлетворяет одно значение x = 0. 3. х Î (1; 2], F (x) = р(x = 0) + P (x = 1) = 1/4 + 1/2 = 3/4,здесь неравенству x < x удовлетворяют два значения x = 0 и x = 1. 4. х Î (2; ∞) F (x) = P (x = 0) + P (x = 1) + P (x = 2) = 1/4 + 1/2 + 1/4 = 1, на этом интервале неравенству x < x удовлетворяют все значения случайной величины. Таким образом, F(x) = График вычисленной функции приведен на Рис.7.
Рис. 7. Квантилью порядка р распределения случайной величины x непрерывного типа называется действительное число x Лекция 7. Математическое ожидание. Случайные величины помимо законов распределения могут описываться также числовыми характеристиками. Математическим ожиданием М (x) случайной величины называется ее среднее значение. Математическое ожидание дискретной случайной величины вычисляется по формуле М (x) = где Рассмотрим свойства математического ожидания: 1. Математическое ожидание константы равно самой константе М (С) = С 2. Если случайную величину умножить на некоторое число k, то и математическое ожидание умножится на это же число М (kx) = kМ (x) 3. Математическое ожидание суммы случайных величин равно сумме их математических ожиданий М (x1 + x2 + … + xn) = М (x1) + М (x2) +…+ М (xn) 4. М (x1 - x2) = М (x1) - М (x2) 5. Для независимых случайных величин x1, x2, … xn математическое ожидание произведения равно произведению их математических ожиданий М (x1, x2, … xn) = М (x1) М (x2) … М (xn)
6. М (x - М (x)) = М (x) - М (М(x)) = М (x) - М (x) = 0 Вычислим математическое ожидание для случайной величины из Примера 11. М (x) = Пример 12. Пусть случайные величины x1, x2 заданы соответственно законами распределения: x1 Таблица 2
x2 Таблица 3
Вычислим М (x1) и М (x2) М (x1) = (- 0,1) 0,1 + (- 0,01) 0,2 + 0 · 0,4 + 0,01 · 0,2 + 0,1 · 0,1 = 0 М (x2) = (- 20) 0,3 + (- 10) 0,1 + 0 · 0,2 + 10 · 0,1 + 20 · 0,3 = 0 Математические ожидания обеих случайных величин одинаковы- они равны нулю. Однако характер их распределения различный. Если значения x1 мало отличаются от своего математического ожидания, то значения x2 в большой степени отличаются от своего математического ожидания, и вероятности таких отклонений не малы. Эти примеры показывают, что по среднему значению нельзя определить, какие отклонения от него имеют место как в меньшую, так и в большую сторону. Так при одинаковой средней величине выпадающих в двух местностях осадков за год нельзя сказать, что эти местности одинаково благоприятны для сельскохозяйственных работ. Аналогично по показателю средней заработной платы не возможно судить об удельном весе высоко- и низкооплачиваемых работниках. Поэтому, вводится числовая характеристика – дисперсия D (x), которая характеризует степень отклонения случайной величины от своего среднего значения: D (x) = M (x - M (x))2 . (2) Дисперсия –это математическое ожидание квадрата отклонения случайной величины от математического ожидания. Для дискретной случайной величины дисперсия вычисляется по формуле: D (x) = Из определения дисперсии следует, что D (x) Свойства дисперсии: 1. Дисперсия константы равна нулю D (C) = 0 2. Если случайную величину умножить на некоторое число k, то дисперсия умножится на квадрат этого числа D (kx) = k2 D (x) 3. D (x) = М (x2) – М2 (x) 4. Для попарно независимых случайных величин x1, x2, … xn дисперсия суммы равна сумме дисперсий. D (x1 + x2 + … + xn) = D (x1) + D (x2) +…+ D (xn) Вычислим дисперсию для случайной величины из Примера 11. Математическое ожидание М (x) = 1. Поэтому по формуле (3) имеем: D (x) = (0 – 1)2·1/4 + (1 – 1)2·1/2 + (2 – 1)2·1/4 =1·1/4 +1·1/4= 1/2 Отметим, что дисперсию вычислять проще, если воспользоваться свойством 3: D (x) = М (x2) – М2 (x). Вычислим дисперсии для случайных величин x1, x2 из Примера 12 по этой формуле. Математические ожидания обеих случайных величин равны нулю. D (x1) = 0,01· 0,1 + 0,0001· 0,2 + 0,0001· 0,2 + 0,01· 0,1 = 0,001 + 0,00002 + 0,00002 + 0,001 = 0,00204 D (x2) = (-20)2 · 0,3 + (-10)2 · 0,1 + 102 · 0,1 + 202 · 0,3 = 240 +20 = 260 Чем ближе значение дисперсии к нулю, тем меньше разброс случайной величины относительно среднего значения. Величина Модой случайной величины x непрерывного типа Md, называется действительное число, определяемое как точка максимума плотности распределения вероятностей f(x). Медианой случайной величины x непрерывного типа Mn называется действительное число, удовлетворяющее уравнению F(x) = Лекция 8. Примеры дискретных распределений. 1. Биноминальное. Пусть произведено n независимых испытаний. В каждом испытании наступает либо событие А, либо Закон распределения этой случайной величины можно записать следующим образом Р (x = m) = Действительно, рассмотрим выражение (p + q)n =1 , разложим двучлен (p + q)n по формуле бинома Ньютона. Получим т.е. сумма вероятностей значений случайной величины равна единице, следовательно (4) является законом распределения. Найдем математическое ожидание: M (x) = Рассмотрим случайные величины x1, x2, … xn, с одинаковым законом распределения: xk = где k = 1,2,…n. Тогда x = x1 + x2 + … + xn. Используя свойства математического ожидания получим: М (x) = М (x1 + x2 + … + xn) = М (x1) + М (x2) +…+ М (xn). Найдем математическое ожидание xk, М (xk) = 0 · (1 – p) + 1· p = р, тогда М (x) = np Аналогично найдем дисперсию: D (x) = D (x1 + x2 + … + xn) = D (x1) + D (x2) +…+ D (xn) D (xk) = (0 – p)2 (1 – p) + (1 – p)2 p = p2 (1 – p) + (1 – p)2 p = = p (1 – p) (p + 1 – p) = p (1 – p) = p q D (x) = n p q,
2. Распределение Пуассона. Пусть произведено бесконечное число испытаний. Рассмотрим случайную величину x -число появлений события А. m = 0, 1, 2,... Закон распределения в данном случае имеет вид: p (x =m) = Покажем, что сумма вероятностей равна единице.
Аналогично можно показать, что математическое ожидание и дисперсия соответственно равны М (x) = Закон Пуассона называют законом редких событий.
Плотность распределения. Плотность распределения вероятностей f(x) характеризует вероятность попадания случайной величины в некоторый интервал. Эта вероятность равна площади, заключенной между осью абсцисс и функцией f(x) на интервале (Рис.8). Функция f(x) =
Рис. 8 Плотность распределения обладает следующими свойствами: 1. f (x) ≥ 0 2. 3. p(a 4. f(x) = Понятие функции распределения, математического ожидания и дисперсии имеет такой же смысл, как в дискретном случае, а вычисляются соответственно по формулам (6) – (8).
M (x) = D ( x) = Пример 13. Случайная величина x распределена по закону, определяемому плотностью распределения вероятностей вида f (x) = Найти параметр a, F(x), M (x), D ( x). Параметр a найдем из свойства
Нарисуем график плотности распределения f (x) (Рис.9)
Рис. 9 Вычислим функцию распределения, для этого рассмотрим интервалы 1. х Î (- ∞, 0) 2. х Î [0, 2] 3. х График функции приведен на Рис. 10. Вычислим математическое ожидание и дисперсию:
Рис.10 Лекция 9. Примеры распределений непрерывной случайной величины. 1. Равномерное распределение. f(x) = Вычислим математическое ожидание и дисперсию:
= Рассмотренное в Примере 13 распределение является равномерным при a = 0 и b = 1. 2. Показательное (экспоненциальное) распределение: Случайная величина x называется распределенной по показательному (экспоненциальному) закону с параметром и ее плотность распределения задается формулой
f(x) = График функции приведен на Рис.11.
Рис. 11. Математическое ожидание и дисперсия соответственно равны: M (x) = 3. Закон нормального распределения. Случайная величина называется распределенной по нормальному закону с параметрами а и f(x) = Для того, чтобы построить график этой функции, проведем ее исследование. Вычислим производную
При x < a График функции приведен на Рис.12. Важное значение в прикладных задачах имеет частный случай плотности нормального распределения при a = 0 и
Для значений этой функции имеются таблицы (Приложение 1).
Рис. 12 Вычислим математическое ожидание и дисперсию:
При вычислении интегралов использованы свойства: 1) 2) Аналогично можно показать, что D (x) = Вероятность попадания случайной величины x в интервал
где
функция нормального распределения N(0,1), д ля этой функции имеются таблицы (Приложение 2). Отметим, что Ф(-x) = 1 - Ф(x) (15) Пример 14. Коробки с шоколадом упаковывают автоматически.Их средняя масса равна 1,06 кг. Известно, что 5 % коробок имеют массу меньше 1 кг. Какой процент коробок, масса которых превышает 940 г. (вес коробок распределен нормально)? Из условия задачи параметр а= 1,06, параметр Рассмотрим случайную величину x - масса коробок. Требуется определить p (x > 0,94), т.е. p (x > 0,94) = p (0,94 < x < + ∞)
Из таблицы Приложения 2 определим
p (0,94 < x < + ∞) Параметр σ найдем из условия р (x < 1) = 0,5
т.е. 1- По таблице Приложения 3 определим
4. Распределение Парето Распределение Парето используется при изучении распределения доходов, превышающих некоторый пороговый уровень x0. f(x) = M(ξ)=
Начальные моменты. Начальным моментом порядка k называется математическое ожидание k-ой степени случайной величины υк = M(ξк), k = 1,2,…n (16) υ1 = M(ξ), первый начальный момент – это математическое ожидание. Центральные моменты Центральным моментом степени k называется математическое ожидание к-ой степени отклонения случайной величины от среднего значения. μк = М (ξ-М(ξ))к (17) μ1 = М (ξ-М(ξ)) = 0 μ2 = М (ξ-М(ξ))2 = D(ξ) Центральные моменты всегда можно выразить через начальные. Например: М2= М(ξ-М(ξ))2 = М (ξ2-2ξМ(ξ)+М2(ξ) = М(ξ2) - М(2ξМ(ξ))+М(М2(ξ)) = М(ξ2)-2М(ξ)М(ξ)+М2(ξ) = М(ξ2) -М2(ξ) = υ2 Центральный момент степени k можно преобразовать к выражению через начальные моменты, используя формулу бинома Ньютона. Запишем формулы для 3-го и 4-го центральных моментов: μ3 = υ3 - 3υ1υ2 + 2υ12 μ4 = υ4 - 4υ1υ3 + 6υ1υ22 - 3υ14 Коэффициент асимметрии
характеризует степень асимметричности распределения. Для симметричного распределения А=0. При А<0 – левосторонняя асимметрия, А>0 – правосторонняя асимметрия.
Коэффициент эксцесса
Рис. 14. Лекция 11.
|
|||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 279; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.216.34.146 (0.243 с.) |
 - это математическая наука, изучающая закономерности случайных явлений. Возникновение теории вероятностей относится к середине XVII века и связано с именами Гюйгенса (1629-1695), Паскаля (1623-1662),Ферма (1601-1665) и Я.Бернулли (1654-1705).В переписке Паскаля и Ферма, вызванной задачами, поставленными азартными играми и не укладывающимися в рамки математики того времени, привели постепенно к таким важным понятиям, как вероятность и математическое ожидание. При этом, конечно, выдающиеся ученые, занимаясь задачами азартных игр, предвидели и фундаментальную роль науки, изучающей случайные явления. Они были убеждены в том, что на базе массовых случайных событий могут возникать четкие закономерности. Формально-математический аппарат, посредством которого решались возникавшие в теории вероятностей задачи, сводился исключительно к элементарным арифметическим и комбинаторным методам.
- это математическая наука, изучающая закономерности случайных явлений. Возникновение теории вероятностей относится к середине XVII века и связано с именами Гюйгенса (1629-1695), Паскаля (1623-1662),Ферма (1601-1665) и Я.Бернулли (1654-1705).В переписке Паскаля и Ферма, вызванной задачами, поставленными азартными играми и не укладывающимися в рамки математики того времени, привели постепенно к таким важным понятиям, как вероятность и математическое ожидание. При этом, конечно, выдающиеся ученые, занимаясь задачами азартных игр, предвидели и фундаментальную роль науки, изучающей случайные явления. Они были убеждены в том, что на базе массовых случайных событий могут возникать четкие закономерности. Формально-математический аппарат, посредством которого решались возникавшие в теории вероятностей задачи, сводился исключительно к элементарным арифметическим и комбинаторным методам. = { 2, 4, 6 }, В = { 4, 5, 6 }, C = { 1, 3, 5 }.
= { 2, 4, 6 }, В = { 4, 5, 6 }, C = { 1, 3, 5 }. .
. <t < Т. Пусть С-событие, состоящее в том, что встреча произойдет. Тогда
<t < Т. Пусть С-событие, состоящее в том, что встреча произойдет. Тогда }
}
 Те элементарные исходы, при которых событие А наступает, называют благоприятствующими событию А.
Те элементарные исходы, при которых событие А наступает, называют благоприятствующими событию А. . состоящее из всех тех точек
. состоящее из всех тех точек  - элементарных событий, которые благоприятствуют событию А.
- элементарных событий, которые благоприятствуют событию А. Событие называется достоверным, если оно в эксперименте заведомо наступит и обозначается
Событие называется достоверным, если оно в эксперименте заведомо наступит и обозначается  В).
В). В), происходящее тогда и только тогда, когда происходит или событие А, или событие В. Сумма событий соответствует объединению множеств, Рис.3.
В), происходящее тогда и только тогда, когда происходит или событие А, или событие В. Сумма событий соответствует объединению множеств, Рис.3.

 -некоторое множество событий то сумма есть событие,происходящее тогда и только тогда, когда происходит хотя бы одно событие.
-некоторое множество событий то сумма есть событие,происходящее тогда и только тогда, когда происходит хотя бы одно событие. В), происхо-
В), происхо- ).
).

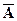 называется противоположным событию А, если оно происходит тогда и только тогда, когда не происходит А (соответствует дополнению множеств) Рис. 6.
называется противоположным событию А, если оно происходит тогда и только тогда, когда не происходит А (соответствует дополнению множеств) Рис. 6.
 , А
, А  ,
,  ,
,  .
. .Примером несовместных событий являются А и
.Примером несовместных событий являются А и  ,А
,А  , …, А
, …, А  составляет полную группу попарно несовместных событий, если:
составляет полную группу попарно несовместных событий, если: =
=  i
i  j, i,j=
j, i,j=  .
.
 0.
0. равна
равна Р(В).
Р(В). , причем исходы эксперимента равновозможны, А={ Г }, таким образом m =1, n =2, P(A) =
, причем исходы эксперимента равновозможны, А={ Г }, таким образом m =1, n =2, P(A) =  .
. -равновозможны, А={4,5,6}, m =3, n =6, P(A) =
-равновозможны, А={4,5,6}, m =3, n =6, P(A) =  .
. , P(A) =
, P(A) =  =
=  =
=  .
. - ¥ F(x)
- ¥ F(x)  .
. ,
, .
.

 , удовлетворяющее уравнению р
, удовлетворяющее уравнению р  = р
= р , (1)
, (1) – значения случайной величины, р i - ихвероятности.
– значения случайной величины, р i - ихвероятности. .
.
 =
=  (3)
(3) называется среднеквадратическим отклонением. Модой случайной величины x дискретного типа Md называется такое значение случайной величины, которому соответствует наибольшая вероятность.
называется среднеквадратическим отклонением. Модой случайной величины x дискретного типа Md называется такое значение случайной величины, которому соответствует наибольшая вероятность. .
.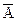 соответственно с вероятностями р, 1 –р. Рассмотрим случайную величину x - число появлений события А в последовательности испытаний.
соответственно с вероятностями р, 1 –р. Рассмотрим случайную величину x - число появлений события А в последовательности испытаний. , m=0,1,2,…n. (4)
, m=0,1,2,…n. (4)
 ,
,

 , λ > 0 - параметр распределения, m = 0, 1, 2,... (5)
, λ > 0 - параметр распределения, m = 0, 1, 2,... (5) .
. ,
,
 .
.


 в точках непрерывности функции f(x).
в точках непрерывности функции f(x). (6)
(6) (7)
(7) (8)
(8)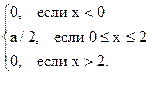
 разобьем на сумму трех интегралов
разобьем на сумму трех интегралов

 .
. ,
, ,
, (2,
(2,  )
)  .
.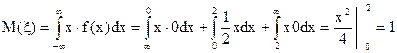


 (9)
(9)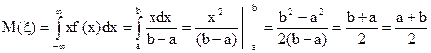 ,
,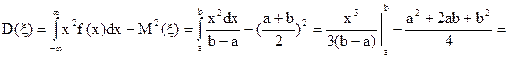
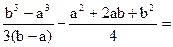
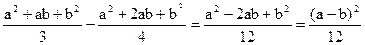
 (10)
(10)
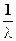 , D (x)=
, D (x)= 
 >0, если плотность распределения вероятностей имеет вид
>0, если плотность распределения вероятностей имеет вид ,
, 
 .
.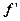 > 0, следовательно на интервале
> 0, следовательно на интервале 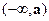 функция возрастает, а при x > a
функция возрастает, а при x > a  . (12) Функция (12) - четная, т.е.
. (12) Функция (12) - четная, т.е.  (-x) =
(-x) = 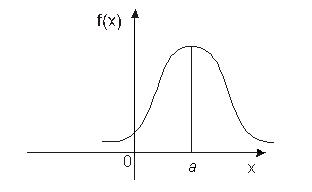

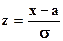 ;
;  ;
;  .
. = 0, как интеграл от нечетной функции в симметричных пределах;
= 0, как интеграл от нечетной функции в симметричных пределах; =1, как интеграл от плотности нормального распределения с параметрами a = 0 и
=1, как интеграл от плотности нормального распределения с параметрами a = 0 и 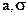 ).
). вычисляется по формуле (13)
вычисляется по формуле (13)  , (13)
, (13) - функция Лапласа
- функция Лапласа , ( 14)
, ( 14)

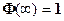 , по формуле (14) имеем
, по формуле (14) имеем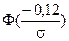 = 1-
= 1- 
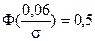 откуда получим
откуда получим  ) = 0,95.
) = 0,95. = 1,645, тогда из равенства
= 1,645, тогда из равенства найдем значение
найдем значение  . Окончательно получим
. Окончательно получим .
. x0 < x < ∞, α > 0, х0 > 0 – параметры распределения.,
x0 < x < ∞, α > 0, х0 > 0 – параметры распределения., , D(ξ)=
, D(ξ)=  .
.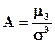 (18)
(18)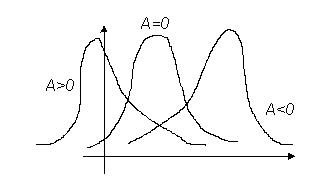
 Рис.13
Рис.13
 (19) характеризует степень островерхости распределения. Для нормального распределения Е=0.
(19) характеризует степень островерхости распределения. Для нормального распределения Е=0.


