
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вероятность отклонения относительной частоты от постоянной вероятности в независимых испытаниях
Вновь будем считать, что производится п независимых испытаний, в каждом из которых вероятность появления события А постоянна и равна р (0< р <1). Поставим перед собой задачу найти вероятность того, что отклонение относительной частоты т/п от постоянной вероятности р по абсолютной величине не превышает заданного числа e > 0. Другими словами, найдем вероятность осуществления неравенства |т/п-p| Эту вероятность будем обозначать так: Р (|т/п-p| - e Умножая эти неравенства на положительный множитель - e Воспользуемся интегральной теоремой Лапласа в форме, указанной в замечании (см. § 3). Положив х' = - e P (- e
Наконец, заменив неравенства, заключенные в скобках, равносильным им исходным неравенством, окончательно получим Р (| т/п —р| Итак, вероятность осуществления неравенства | т/п —р| Пример 1. Вероятность того, что деталь не стандартна, р = 0,1. Найти вероятность того, что среди случайно отобранных 400 деталей относительная частота появления нестандартных деталей отклонится от вероятности р = 0,1 по абсолютной величине не более чем на 0,03. Решение. По условию, n = 400; р = 0,1; q = О,9; e = 0,03. Требуется найти вероятность Р (| m /400—0,1 | Р (| т/п —р| Р (|m/ 400 — 0, 1 | По таблице приложения 2 находим Ф (2) = 0,4772. Следовательно, 2Ф (2) = 0,9544. Итак, искомая вероятность приближенно равна 0,9544. Смысл полученного результата таков: если взять достаточно большое число проб по 400 деталей в каждой, то примерно в 95,44% этих проб отклонение относительной частоты от постоянной вероятности p = 0,1 по абсолютной величине не превысит 0,03. Пример 2. Вероятность того, что деталь не стандартна, р = 0,1. Найти, сколько деталей надо отобрать, чтобы с вероятностью, равной 0,9544, можно было утверждать, что относительная частота появления нестандартных деталей (среди отобранных) отклонится от постоянной вероятности р по абсолютной величине не более чем на 0,03. Решение. По условию, р =0,1; q = 0,9; e = 0,03; Р (| т/п — 0, 1 | Требуется найти n.
Воспользуемся формулой Р (| т/п —р| В силу условия 2 Ф (0, 03 Следовательно, Ф (0, 1 По таблице приложения 2 находим Ф (2) = 0,4772. Для отыскания числа n получаем уравнение 0,1 Смысл полученного результата таков: если взять достаточно большое число проб по 400 деталей, то в 95,44% этих проб относительная частота появления нестандартных деталей будет отличаться от постоянной вероятности р = 0,1 по абсолютной величине не более чем на 0,03, т. е. относительная частота заключена в границах от 0,07(0,1—0,03 = 0,07) до 0,13(0,1+0,03 = 0,13). Другими словами, число нестандартных деталей в 95,44% проб будет заключено между 28(7% от 400) и 52(13% от 400). Если взять лишь одну пробу из 400 деталей, то с большой уверенностью можно ожидать, что в этой пробе будет нестандартных деталей не менее 28 и не более 52. Возможно, хотя и маловероятно, что нестандартных деталей окажется меньше 28 либо больше 52.
Задачи 1. В цехе 6 моторов. Для каждого мотора вероятность того, что он в данный момент включен, равна 0,8. Найти вероятность того, что в данный момент: а) включено 4 мотора; б) включены все моторы; в) выключены все моторы. Отв. Р 6(4) = 0,246; б) Р 6(6) = 0,26; в) Р 6 (0) = 0,000064. 2. Найти вероятность того, что событие А появится в пяти независимых испытаниях не менее двух раз, если в каждом испытании вероятность появления события А равна 0,3. Отв. Р =1-[ Р 5(0) + Р 5 (1)] = 0,472. 3. Событие В появится в случае, если событие А появится не менее двух раз. Найти вероятность того, что наступит событие В, если будет произведено 6 независимых испытаний, в каждом из которых вероятность появления события А равна 0,4. Отв. Р =1 —[ Р 6(0) + Р 6(1)] =0,767. 4. Произведено 8 независимых испытаний, в каждом из которых вероятность появления события A равна 0,1. Найти вероятность того, что событие А появится хотя бы 2 раза. Отв. Р=1-[ Р 8(0)+ Р 8 (1)] = 0,19. 5. Монету бросают 6 раз. Найти вероятность того, что герб выпадет: а) менее двух раз; б) не менее двух раз. Отв. а) Р = Р 6 (0) + Р 6 (1) = 7/64; 6) Q = 1 — [ P 6(0)+ P 6(l)] = 57/64. 6. Вероятность попадания в цель при одном выстреле из орудия р = 0,9. Вероятность поражения цели при к попаданиях (k
Указание. Воспользоваться формулами Бернулли и полной вероятности. Отв. 0,9639. 7. Найти приближенно вероятность того, что при 400 испытаниях событие наступит ровно 104 раза, если вероятность его появления в каждом испытании равна 0,2. Отв. Р 400 (104) =0,0006. 8. Вероятность поражения мишени стрелком при одном выстреле равна 0,75. Найти вероятность того, что при 100 выстрелах мишень, будет поражена: а) не менее 70 и не более 80 раз; б) не более 70 раз. Отв. а) Р 100 (70,80) = 2 Ф (1,15) =0,7498; б) Р 100(0; 70)= —Ф (1,15) + 0,5 = 0,1251. 9. Вероятность появления события в каждом из 10 000 независимых испытаний p = 0,75. Найти вероятность того, что относительная частота появления события отклонится от его вероятности по абсолютной величине не более чем на 0,001. Отв. Р = 2 Ф (0,23)=0,182. 10. Вероятность появления события в каждом из независимых испытаний равна 0,2. Найти, какое отклонение относительной частоты появления события от его вероятности можно ожидать с вероятностью 0,9128 при 5000 испытаниях. Отв. e = 0,00967. 11. Сколько раз надо бросить монету, чтобы с вероятностью 0,6 можно было ожидать, что отклонение относительной частоты появлений герба от вероятности р = 0,5 окажется по абсолютной величине не более 0,01? Отв. п =1764.
ЧАСТЬ ВТОРАЯ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ Глава шестая ВИДЫ СЛУЧАЙНЫХ ВЕЛИЧИН. ЗАДАНИЕ ДИСКРЕТНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ
Случайная величина Уже в первой части приводились события, состоящие в появлении того или иного числа. Например, при бросании игральной кости могли появиться числа 1, 2, 3, 4, 5 и 6. Наперед определить число выпавших очков невозможно, поскольку оно зависит от многих случайных причин, которые полностью не могут быть учтены. В этом смысле число очков есть величина случайная; числа 1, 2, 3, 4, 5 и 6 есть возможные значения этой величины. Случайной называют величину, которая в результате испытания примет одно и только одно возможное значение, наперед не известное и зависящее от случайных причин, которые заранее не могут быть учтены. Пример 1. Число родившихся мальчиков среди ста новорожденных есть случайная величина, которая имеет следующие возможные значения: 0, 1, 2,..., 100. Пример 2. Расстояние, которое пролетит снаряд при выстреле из орудия, есть случайная величина. Действительно, расстояние зависит не только от установки прицела, но и от многих других причин (силы и направления ветра, температуры и т. д.), которые не могут быть полностью учтены. Возможные значения этой величины принадлежат некоторому промежутку (а, b). Будем далее обозначать случайные величины прописными буквами X, Y, Z, а их возможные значения — соответствующими строчными буквами х, у, z. Например, если случайная величина X имеет три возможных значения, то они будут обозначены так: х 1, х 2, х 3.
|
||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 1641; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.33.153 (0.019 с.) |
 e (*)
e (*)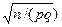 , получим неравенства, равносильные исходному:
, получим неравенства, равносильные исходному:

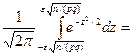
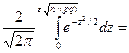 2 Ф (e
2 Ф (e 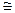 2 Ф (e
2 Ф (e  2 Ф (2).
2 Ф (2).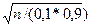 = 2 Ф (0, 1
= 2 Ф (0, 1 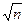 ) = 0, 9544.
) = 0, 9544. 1) равна 1— qk. Найти вероятность того, что цель будет поражена, если сделано два выстрела.
1) равна 1— qk. Найти вероятность того, что цель будет поражена, если сделано два выстрела.


