Разработка математической модели

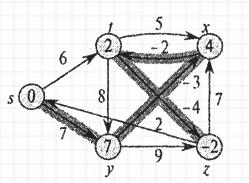
Анализ источников [1-5,14,19,23-26] показал, что для нахождения оптимального пути маршрута кабеля при создании ЛВС необходимо оценить существующие алгоритмы поиска кратчайшего пути. Рассмотрим 5 наиболее популярных алгоритмов:

1. Алгоритм Беллмана-Форда.

2. Алгоритм Флойда – Уоршелла.

3. Алгоритм Дейкстры.

4. Алгоритмом Йена.

5. Волновой алгоритм.

Алгоритм Беллмана-Форда позволяет решить задачу о кратчайшем пути из одной вершины в общем случае, когда вес каждого из ребер может быть отрицательным. Для заданного взвешенного ориентированного графа G = (V, Е) с истоком s и весовой функцией w: Е —» R алгоритм Беллмана-Форда возвращает логическое значение, указывающее на то, содержится ли в графе цикл с отрицательным весом, достижимый из истока. Если такой цикл существует, в алгоритме указывается, что решения не существует. Если же таких циклов нет, алгоритм выдает кратчайшие пути и их вес.

В этом алгоритме используется ослабление, в результате которого величина d[v], представляющая собой оценку веса кратчайшего пути из истока s к каждой из вершин v є V, уменьшается до тех пор, пока она не станет равна фактическому весу кратчайшего пути из s в v. Значение TRUE возвращается алгоритмом тогда и только тогда, когда граф не содержит циклов с отрицательным весом, достижимых из истока.

Bellman_Ford(G, w, s)

1 Initialize_Single_Source(G, s)

2 for i «- l to |V[G]|-1

3 do for (для) каждого ребра (u, v) є E[G]

4 do RELAX(u,v,w)

5 for (для) каждого ребра (u, v) є E[G]

6 do if d[v] > d[u] + w(u, v)

7 then return FALSE

8 return TRUE

После инициализации в строке 1 всех значений d и prev, алгоритм осуществляет |V| — 1 проходов по ребрам графа. Каждый проход соответствует одной итерации цикла for в строках 2-4 и состоит из однократного ослабления каждого ребра графа. После |V| — 1 проходов в строках 5-8 проверяется наличие цикла с отрицательным весом и возвращается соответствующее булево значение.

Алгоритм Беллмана-Форда завершает свою работу в течение времени O(V*E), поскольку инициализация в строке 1 занимает время O(V), на каждый из |V| — 1 проходов по ребрам в строках 2-4 требуется время в O(E), а на выполнение цикла for в строках 5-7 — время O(Е).

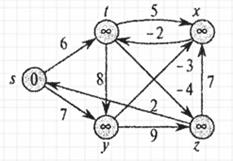
Рисунок 2.3. – Пример графа по алгоритму Беллмана-Форда

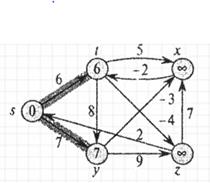
Рисунок 2.4. – Пример графа по алгоритму Беллмана-Форда после первого прохода по ребрам

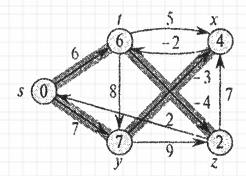
Рисунок 2.5. – Пример графа по алгоритму Беллмана-Форда после второго прохода по ребрам

 

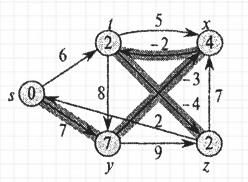
Рисунок 2.6. – Пример графа по алгоритму Беллмана-Форда после третьего прохода по ребрам

 

Рисунок 2.7. – Пример графа по алгоритму Беллмана-Форда после четвертого прохода по ребрам

На рисунках 2.3 - 2.7 в вершинах графа показаны значения атрибутов d на каждом этапе работы алгоритма, а выделенные ребра указывают на значения предшественников: если ребро (u, v) выделено, то prev[v] = u. В рассматриваемом примере при каждом проходе ребра ослабляются в следующем порядке: (t, х), (t, у), (t, z), (x,t), (у,х), (у, z), (z,x), (z,s), (s,t), (s,y). Рисунок 2.3 показывает ситуацию, сложившуюся непосредственно перед первым проходом по ребрам. В рисунках 2.4 - 2.7 проиллюстрирована ситуация после каждого очередного прохода по ребрам. Значения атрибутов d и prev, приведенные на рисунке 2.7, являются окончательными [30].

Алгоритм Флойда - Уоршелла — динамический алгоритм для нахождения кратчайших расстояний между всеми вершинами взвешенного ориентированного графа. Разработан в 1962 году Робертом Флойдом и Стивеном Уоршеллом [ 29].

Более строгая формулировка этой задачи следующая: есть ориентированный граф G = (V, Е) каждой дуге v -> w этого графа сопоставлена неотрицательная стоимость C[v, w]. Общая задача нахождения кратчайших путей заключается в нахождении для каждой упорядоченной пары вершин v, w) любого пути от вершины v в вершины w, длина которого минимальна среди всех возможных путей от v к w.

Для определенности положим, что вершины графа последовательно пронумерованы от 1 до n. Алгоритм Флойда использует матрицу А размера п * n, в которой вычисляются длины кратчайших путей. Вначале A[i, j] = C[i, j] для всех i!= j. Если дуга i -» j отсутствует, то C[i, j] = infinity. Каждый диагональный элемент матрицы А равен 0.

Над матрицей А выполняется п итераций. После k-й итерации A[i, j] содержит значение наименьшей длины путей из вершины i в вершину у, которые не проходят через вершины с номером, большим k. Другими словами, между концевыми вершинами пути i и у могут находиться только вершины, номера которых меньше или равны k. На k-й итерации для вычисления матрицы А применяется следующая формула:

Ak[i,j]=min(Ak-1[i,j], Ak-1[i,k]+Ak-1[k,j]) (2.1)

Нижний индекс k обозначает значение матрицы А после k-й итерации, но это не означает, что существует п различных матриц, этот индекс используется для сокращения записи. Для вычисления Ak[i, j] проводится сравнение величины Ak-i[i, j] (т.е. стоимость пути от вершины i к вершине j без участия вершины k или другой вершины с более высоким номером) с величиной Ak-1[i, k] + Ak-1[k, j] (стоимость пути от вершины i до вершины k плюс стоимость пути от вершины k до вершины j). Если путь через вершину k дешевле, чем Ak-1[i, j], то величина Ak[i, j] изменяется.

Время выполнения этой программы, очевидно, имеет порядок 0(V3), поскольку в ней практически нет ничего, кроме вложенных друг в друга трех циклов. Доказательство "правильности" работы этого алгоритма также очевидно и выполняется с помощью математической индукции по k, показывая, что на k-й итерации вершина k включается в путь только тогда, когда новый путь короче старого.

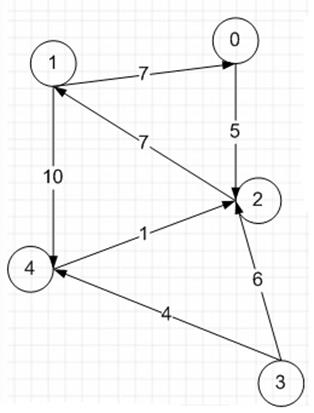
Рисунок 2.8. – Пример графа по алгоритму Флойда – Уоршелла

На таблице 2.1 представлена таблица расстояний по графу из рисунка 2.8.

Таблица 2.1 – Таблица расстояний для графа по алгоритму Флойда-Уоршелла

				-
				-
				-
				-

 

Алгоритм Дейкстры — алгоритм на графах, изобретённый нидерландским ученым Э. Дейкстрой в 1959 году. Находит кратчайшее расстояние от одной из вершин графа до всех остальных. Алгоритм работает только для графов без рёбер отрицательного веса.

Dijkstra(G, w, s)

1 Initialize_Single_Source(G, s)

2 S← 0

3 Q←V[G]

4 while Q<>0

5 do u←Extract_MIN(Q)

6 S← Sﮟ [u]

7 for (для) каждой вершины v є Adj[u]

8 do Relax(u,v,w)

В строке 1 производится обычная инициализация величин d и pi, а в строке 2 инициализируется пустое множество вершин S. В этом алгоритме поддерживается инвариант, согласно которому в начале каждой итерации цикла while в строках 4-8 выполняется равенство Q = V — S. В строке 3 неубывающая очередь с приоритетами Q инициализируется таким образом, чтобы она содержала все вершины множества V; поскольку в этот момент S = 0, после выполнения строки 3 сформулированный выше инвариант выполняется. При каждой итерации цикла while в строках 4-8 вершина и извлекается из множества Q = V — S и добавляется в множество 5, в результате чего инвариант продолжает соблюдаться. (Во время первой итерации этого цикла u = s.) Таким образом, вершина и имеет минимальную оценку кратчайшего пути среди всех вершин множества V — 5. Затем строках 7-8 ослабляются все ребра (u, v), исходящие из вершины и. Если текущий кратчайший путь к вершине v может быть улучшен в результате прохождения через вершину и, выполняется ослабление и соответствующее обновление оценки величины d [v] и предшественника тг [v]. Обратите внимание, что после выполнения строки 3 вершины никогда не добавляются в множество Q и что каждая вершина извлекается из этого множества и добавляется в множество 5 ровно по одному разу, поэтому количество итераций цикла while в строках 4-8 равно | V|. Поскольку в алгоритме Дейкстры из множества V — S для помещения в множество 5 всегда выбирается самая "легкая" или "близкая" вершина, говорят, что этот алгоритм придерживается жадной стратегии.

Время выполнения алгоритма Дейкстры зависит от реализации неубывающей очереди с приоритетами. Сначала рассмотрим случай, когда неубывающая очередь с приоритетами поддерживается за счет того, что все вершины пронумерованы от 1 до |V|. Атрибут d[v] просто помещается в элемент массива с индексом v. Каждая операция Insert и Decrease_Key (неявно присутствует в процедуре Relax) занимает время 0(1), а каждая операция Extract_Min — время О (V) (поскольку в ней производится поиск по всему массиву); в результате полное время работы алгоритма равно О (V2 + Е) = О(V2).

Если граф достаточно разреженный, в частности, если количество вершин и ребер в нем связаны соотношением Е = o(V2/lgV), с практической точки зрения целесообразно реализовать неубывающую очередь с приоритетами в виде бинарной неубывающей пирамиды. (важная деталь реализации заключается в том, что вершины и соответствующие им элементы пирамиды должны поддерживать идентификаторы друг друга.) Далее, каждая операция Extract_Min занимает время О (lg V), Как и раньше, таких операций |V|. Время, необходимое для построения неубывающей пирамиды, равно O(V). Каждая операция Decrease_Key занимает время O(lgV), и всего выполняется не более |Е| таких операций. Поэтому полное время выполнения алгоритма равно О ((V + Е) lg V), что равно О (Е*lg V), если все вершины достижимы из истока. Это время работы оказывается лучшим по сравнению со временем работы прямой реализации О (V2), если Е = о (V2/lg V).

Самый распространенный пример подобных задач, это нахождение кратчайшего расстояния между двумя вершинами. В этом случае, весом дуги (хi, хj) будет являться расстояние между вершинами хi и хj, ну, а если такая дуга отсутствует, то ее вес полагается равным бесконечности (на практике - это максимальное число, возможное на данном языке программирования).

Наиболее эффективный алгоритм решения задачи о кратчайшем (s-t)-пути первоначально предложил Дейкстра (1959г.). В общем случае этот метод основан на приписывании вершинам временных пометок, причем пометка вершины дает верхнюю границу длины от s к этой вершине. Эти пометки (их величины) постепенно уменьшаются с помощью некоторой итерационной процедуры, и на каждом шаге итерации одна из временных пометок становится постоянной. Последнее указывает на то, что пометка уже не является временной, а дает точную длину кратчайшего пути от s к рассматриваемой вершине.

Только что описанный алгоритм Дейкстры применим для нахождения кратчайшего пути между двумя заданными вершинами s и t. Что бы найти кратчайшие пути между всеми парами вершин, можно n-раз воспользоваться алгоритмом Дейкстры, причем каждый раз в качестве начальной вершины s будут браться различные вершины. В этом случае время, необходимое для вычислений, будет пропорционально n3. Поэтому, если задача о нахождении кратчайшего пути имеет большую размерность, то ее не возможно решить с помощью последовательного применения этого алгоритма.

Есть совершенно иной подход к задаче нахождения кратчайших путей между всеми парами вершин. Он сэкономит почти 50% времени по сравнению с n-кратным применением алгоритма Дейкстры. Метод был предложен первоначально Флойдом (1962 г.) и развит Мерчлендом. Он базируется на использовании последовательности из n преобразований (итераций) начальной матрицы весов С. При этом на k-й итерации матрица представляет длины кратчайших путей между каждой парой вершин с тем ограничением, что путь между xi и xj (для любых xi и xj) содержит в качестве промежуточных только вершины из множества {x1, x2,..., xk}.

На практике часто требуется найти не только кратчайший путь, но также второй, третий и т. д. кратчайшие пути в графе. Располагая этими результатами, можно решить, какой путь выбрать в качестве наилучшего. Для решения этой задачи нужно воспользоваться алгоритмом Йена (1971г.). Этот алгоритм требует порядка Kn3 операций [30].

Существует тип алгоритмов, который в американской литературе фигурирует под названием backtracking algorithms, что в переводе означает “алгоритмы с откатом”. Как правило, такие алгоритмы строятся на основе рекурсии. Эти алгоритмы отличаются от других тем, что ищут решения методом проб и ошибок, перебирая все или почти все варианты.

Backtracking используется в тех случаях, когда более интеллектуальные решения невозможны. Количество таких задач ограничено. Например, поиск оптимума с полным перебором всех вариантов, поиск любого решения с выходом при его отыскании или поиск оптимального решения с оптимизацией полного перебора (отсечением вариантов, которые заведомо хуже ранее найденного оптимального решения). К такому методу относится волновой алгоритм.

Основная часть алгоритма — построение на основе массива множества точек, до которых можно добраться за К шагов и нельзя быстрее (этот процесс аналогичен процессу распространения волны, откуда и произошло название алгоритма).

В рамках рассмотрения задачи о поиске кратчайшего пути между двумя точками в лабиринте более целесообразным является использование волнового алгоритма. Его преимуществами являются: лёгкость переноса с карты лабиринта на массив, т.е. простота построения модели задачи, простота понимания самого алгоритма, быстродействие, а также то, что если пути нет, то это становится известным на определённом шаге и алгоритм дальше не выполняется.

Волновой алгоритм — алгоритм, позволяющий найти минимальный путь в графе с рёбрами единичной длины. Основан на алгоритме поиска в ширину. Применяется для нахождения кратчайшего пути в графе, в общем случае находит лишь его длину.

На двумерной клетчатой карте (матрице), состоящей из «проходимых» и «непроходимых» клеток, обозначена клетка старта и клетка финиша. Цель алгоритма — проложить кратчайший путь от клетки старта к клетке финиша, если это, конечно, возможно. От старта во все направления распространяется волна, причем каждая пройденная волной клетка помечается как «пройденная». Волна, в свою очередь, не может проходить через клетки, помеченные как «пройденные» или «непроходимые». Волна движется, пока не достигнет точки финиша или пока не останется непройденных клеток. Если волна прошла все доступные клетки, но так и не достигла клетки финиша, значит, путь от старта до финиша проложить невозможно. После достижения волной финиша, от финиша прокладывается путь до старта и сохраняется в массиве [21].

Анализ выше описанных алгоритмов показал приемущества и недостатки каждого из них, для комфортного просмотра представим данные в таблице 2.2.

 

Таблица 2.2 – Описание и использование алгоритмов поиска кратчайшего пути

Название алгоритма	Краткое описание	Использование алгоритма
1. Алгоритм Беллмана - Форда.	алгоритм поиска кратчайшего пути во взвешенном графе	В графе с отрицательным весом ребер
2. Алгоритм Флойда – Уоршелла.	динамический алгоритм для нахождения кратчайших расстояний между всеми вершинами взвешенного ориентированного графа	Поиска транзитивного замыкания графа, заканчивая генетикой и управлением проектами, а также транспортные сети
3. Алгоритм Дейкстры.	находит кратчайшее расстояние от одной из вершин графа до всех остальных.	Компьютерные сети, создание планов эвакуации, компьютерные игры
4. Алгоритмом Йена.	нахождения заданного числа кратчайших путей в графе	Компьютерные сети, создание планов эвакуации, компьютерные игры
5. Волновой алгоритм.	анализ пути прохождения сферической волны по изображению	В компьютерных играх для определения минимального расстояния от одного объекта до другого в ограниченном дискретном пространстве