
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Равномерное прямолинейное движениеСтр 1 из 13Следующая ⇒
Равномерное прямолинейное движение Равномерным прямолинейным движением называется такое прямолинейное движение, при котором материальная точка (тело) движется по прямой и в любые равные промежутки времени совершает одинаковые перемещения. Вектор скорости равномерного прямолинейного движения материальной точки направлен вдоль ее траектории в сторону движения. Вектор скорости при равномерном прямолинейном движении равен вектору перемещения за любой промежуток времени, поделенному на этот промежуток времени:
Примем линию, по которой движется материальная точка, за ось координат ОХ, причем за положительное направление оси выберем направление движения точки. Тогда, спроецировав векторы r и v, на эту ось, для проекций ∆rx = |∆r| и ∆vx = |∆v| этих векторов мы можем записать:
Т.к. при равномерном прямолинейном движении S = |∆r|, можем записать: Sx = Vx · t. Тогда для координаты тела в любой момент времени имеем:
где - координата тела в начальный момент t = 0. Равнопеременное прямолинейное движение Равнопеременным называется движение, при котором скорость тела (материальной точки) за любые равные промежутки времени изменяется одинаково, т.е. на равные величины. Это движение может быть равноускоренным и равнозамедленным. Если направление ускорения а совпадает с направлением скорости V точки, движение называется равноускоренным. Если направление векторов а и V противоположны, движение называется равнозамедленным. При равнопеременном прямолинейном движении ускорение остается постоянным и по модулю и по направлению (а = const). При этом среднее ускорение аср равно мгновенному ускорению а вдоль траектории точки. Нормальное ускорение при этом отсутствует (аn=0). Изменение скорости ∆v = v - v0 в течении промежутка времени ∆t = t - t0 при равнопеременном прямолинейном движении равно: ∆v = a·∆t, или v - v0 = a·(t - t0). Если в момент начала отсчета времени (t0) скорость точки равна v0 (начальная скорость) и ускорение а известно, то скорость v в произвольный момент времени t: v = v0 + a·t. Проекция вектора скорости на ось ОХ связана с соответствующими проекциями векторов начальной скорости и ускорения уравнением: vх = v0х ± aх·t. Аналогично записываются уравнения для проекций вектора скорости на другие координатные оси.
Вектор перемещения ∆r точки за промежуток времени ∆t = t - t0 при равнопеременном прямолинейном движении с начальной скоростью v0 и ускорением а равен:
а его проекция на ось ОХ (или перемещение точки вдоль соответствующей оси координат) при t0 = 0 равна:
Путь Sx, пройденный точкой за промежуток времени ∆t = t - t0 в равнопеременном прямолинейном движении с начальной скоростью v0 и ускорением а, при t0 = 0 равен:
Так как координата тела равна х = х0 + S, то уравнение движения тела имеет вид:
Возможно так же при решении задач использовать формулу:
2. Скорость и ускорение. Нормальное и касательное ускорение.
Скорость и ускорение. Вычисление пройденного пути. Скорость – векторная физическая величина, которая определяет как быстроту движения, так и его направление в данный мом вр. Вектор средней скорости за интервал времени – отношение приращения радиус-вектора точки к промеж вр: Силы инерции. Сила инерции – векторная величина, численно равная произведению мат точки на ее ускорение (ускорение НИСО) и направленная противоположно ускорению. 1). тело покоится во вращающейся с пост угл скоростью в НИСО:
3). Тело движется во вращающейся с пост Си́ла Кориоли́са — одна из сил инерции, существующая в неинерциальной системе отсчёта из-за вращения и законов инерции, проявляющаяся при движении в направлении под углом к оси вращения. Названа по имени французского учёного Гюстава Гаспара Кориолиса, впервые её описавшего. Ускорение Кориолиса было получено Кориолисом в 1833 году, Гауссом в 1803 году и Эйлеромв 1765 году. Причина появления силы Кориолиса — в кориолисовом (поворотном) ускорении. В инерциальных системах отсчёта действует закон инерции, то есть, каждое тело стремится двигаться по прямой и с постоянной скоростью. Если рассмотреть движение тела, равномерное вдоль некоторого вращающегося радиуса и направленное от центра, то станет ясно, что чтобы оно осуществилось, требуется придавать телу ускорение, так как чем дальше от центра, тем должна быть больше касательная скорость вращения. Это значит, что с точки зрения вращающейся системы отсчёта, некая сила будет пытаться сместить тело с радиуса. Для того, чтобы тело двигалось с кориолисовым ускорением, необходимо приложение силы к телу, равной Если вращение происходит по часовой стрелке, то двигающееся от центра вращения тело будет стремиться сойти с радиуса влево. Если вращение происходит против часовой стрелки — то вправо. Сила Кориолиса в природе Сила Кориолиса, вызванная вращением Земли, может быть замечена при наблюдении за движением маятника Фуко[1]. Кроме того, сила Кориолиса проявляется и в глобальных масштабах. В северном полушарии сила Кориолиса направлена вправо от движения, поэтому правые берега рек в Северном полушарии более крутые — их подмывает вода под действием этой силы[2] (см. Закон Бэра). В Южном полушарии всё происходит наоборот. Сила Кориолиса ответственна также и за вращение циклонов и антициклонов[3] (см. геострофический ветер): в Северном полушарии вращение воздушных масс происходит в циклонах против часовой стрелки, а в антициклонах — по стрелке; в Южном — наоборот: по часовой стрелке в циклонах и против — в антициклонах. Отклонение ветров (пассатов) при циркуляции атмосферы — также проявление силы Кориолиса.
Если бы рельсы были бы идеальными, то при движении железнодорожных составов с севера на юг и с юга на север, под воздействием силы Кориолиса один рельс изнашивался бы сильнее, чем второй. В северном полушарии больше изнашивается правый, а в южном левый[4]. Силу Кориолиса необходимо учитывать при рассмотрении планетарных движений воды в океане. Она является причиной возникновения гироскопических волн[5]. При идеальных условиях сила Кориолиса определяет направление закручивания воды например, при сливе в раковине. Однако идеальные условия трудно достижимы. Поэтому феномен «обратного закручивания воды при стоке» является скорее околонаучной шуткой. 11) Импульс. Вывод закона сохранения импульса из второго закона динамики. Центр масс системы материальных точек. Импульсом, или количеством движения материальной точки называется векторная величина, равная произведению массы материальной точки m на скорость ее движения v. – для материальной точки; – для системы материальных точек (через импульсы этих точек); – для системы материальных точек (через движение центра масс). Центром масс системы называется точка С, радиус-вектор rC которой равен ,где Уравнение движения центра масс:
Смысл уравнения таков: произведение массы системы на ускорение центра масс равно геометрической сумме внешних сил, действующих на тела системы. Как видим, закон движения центра масс напоминает второй закон Ньютона. Если внешние силы на систему не действуют или сумма внешних сил равна нулю, то ускорение центра масс равно нулю, а скорость его неизменна во времени по модулю и наплавлению, т.е. в этом случае центр масс движется равномерно и прямолинейно. В частности, это означает, что если система замкнута и центр масс ее неподвижен, то внутренние силы системы не в состоянии привести центр масс в движение. На этом принципе основано движение ракет: чтобы ракету привести в движение, необходимо выбросить выхлопные газы и пыль, образующиеся при сгорании топлива, в обратном направлении. Закон Сохранения Импульса Для вывода закона сохранения импульса рассмотрим некоторые понятия. Совокуп ность материальных точек (тел), рассмат риваемых как единое целое, называется механической системой. Силы взаимодей ствия между материальными точками ме ханической системы называются внутрен ними. Силы, с которыми на материальные точки системы действуют внешние тела, называются внешними. Механическая система тел, на которую не действуют
внешние силы, называется замкнутой (или изолированной). Если мы имеем механиче скую систему, состоящую из многих тел, то, согласно третьему закону Ньютона, силы, действующие между этими телами, будут равны и противоположно направле ны, т. е. геометрическая сумма внутренних сил равна нулю. Рассмотрим механическую систему, состоящую из n тел, масса и скорость которых соответственно равны т 1, m 2,..., тn и v 1, v 2,..., v n. Пусть F '1, F '2,..., F 'n — равнодействующие внутренних сил, действующих на каждое из этих тел, a f 1, f 2,..., F n — равнодействующие внешних сил. Запишем второй закон Ньютона для каждого из n тел механической системы: d/dt(m1v1)= F '1+ F 1, d/dt(m2v2)= F' 2+ F 2, d/dt(mn v n)= F 'n+ F n. Складывая почленно эти уравнения, получим d/dt (m1 v 1+m2 v 2+... + mn v n) = F '1+ F '2+...+ F ' n + F 1+ F 2+...+ F n. Но так как геометрическая сумма внутрен них сил механической системы по третьему закону Ньютона равна нулю, то d/dt(m1v1+m2v2 +... + mnvn)= F 1 + F 2+...+ F n, или dp/dt= F 1+ F 2+...+ F n, (9.1) где импульс системы. Таким образом, производная по времени от им пульса механической системы равна гео метрической сумме внешних сил, действующих на систему.
В случае отсутствия внешних сил (рассматриваем замкнутую систему)
Это выражение и является законом сохранения импульса: импульс замкнутой системы сохраняется, т. е. не изменяется с течением времени. Закон сохранения импульса справед лив не только в классической физике, хотя он и получен как следствие законов Ньютона. Эксперименты доказывают, что он выполняется и для замкнутых систем микрочастиц (они подчиняются законам квантовой механики). Этот закон носит универсальный характер, т. е. закон со хранения импульса — фундаментальный закон природы. 12. Физические основы космических полетов: законы движения тел переменной массы.
Пусть в результате этого процесса за время dt скорость ракеты изменится на величину d υ, а ее масса m уменьшится на dm. Тогда изменение импульса системы "ракета, топливо" можно рассчитать с помощью соотношения: d p = ((m - dm)·(υ + d υ) + dm· u) - m· υ, Согласно закону преобразования скоростей, запишем следующее векторное равенство: u = υ т + υ, Из уравнений (14), (15) получим формулу для расчета изменения импульса системы за время dt. d p = m·d υ + υ т·dm. Согласно второму закону Ньютона скорость изменения импульса равна равнодействующей внешних сил F, действующих на систему. Проведя разделение переменных, преобразуем уравнение (16) к виду: d υ = - υ т·dm/m. Проведя интегрирование (17) по скорости от 0 до υ и массе от m0 до m, получим формулу Циолковского (18), позволяющую рассчитать скорость ракеты в зависимости от соотношения масс ракеты с топливом в начальный m0 и текущий m моменты времени и скорости истечения продуктов сгорания топлива относительно ракеты:
υ = υт·ln (m0/m). Формулу (18) можно привести к виду, позволяющему определить, каково должно быть отношение массы ракеты с топливом к массе корпуса ракеты mкдля достижения ракетой заданной скорости υ, например, первой космической.
Работа консервативных сил. Тело, находясь в потенциальном поле сил, обладает потенциальной энергией П. Работа консервативных сил при элементарном (бесконечно малом) изменении конфигурации системы равна приращению потенциальной энергии, взятому со знаком минус, т.к. работа совершается за счет убыли потенциальной энергии: dA = - dП Работа dA выражается как скалярное произведение силы F на перемещение Потенциальная энергия тела. Потенциальная энергия: энергия, обусловленная взаимным расположением тел или частей тела, зависящая от их взаимного положения во внешнем силовом поле. - Сил тяжести:энергия возможного действия гравитационного поля Земли на материальную точку, расположенную на высоте h над уровнем моря. - Упругой деформации: запас энергии деформированного упругого тела. Элементарная работа dA, совершаемая силой Fx при бесконечно малой деформации dx, равна 15. Закон сохранения энергии для системы материальных точек. Применение закона сохранения импульса и закона сохранения энергии к анализу абсолютно упругого и абсолютно неупругого центрального удара (2 часа). Если тела, составляющие замкнутую механическую систему, взаимодействуют между собой только силами тяготения и упругости, то работа этих сил равна изменению потенциальной энергии тел, взятому с противоположным знаком:
По теореме о кинетической энергии эта работа равна изменению кинетической энергии тел (см. §1.19):
Следовательно
Постулат или принцип постоянства скорости света: скорость света в вакууме постоянна и одинакова по отношении» к любым инерциальным системам отсчета. Она не зависит ни от скорости источника света, ни от скорости его приемника. Ни один материальный объект не может двигаться со скоростью, превышающей скорость света в вакууме. Более того, пи одна частица вещества, т.е. частица с массой покоя, отличной от нуля, не может достичь скорости света в вакууме, с такой скоростью могут двигаться лишь полевые частицы, т.е. частицы с массой покоя, равной нулю. Анализируя 1 постулат Эйнштейна, мы видим, что Эйнштейн расширил рамки принципа относительности Галилея, распространив его на любые физические явления, в том числе и на электромагнитные. 1 постулат Эйнштейна непосредственно вытекает из опыта Майкельсона-Морли, доказавшего отсутствие в природе абсолютной системы отсчета. Из результатов этого нее опыта следует и 2 постулат Эйнштейна о постоянстве скорости света в вакууме, который тем не менее вступает в противоречие с 1 постулатом, если распространить на электромагнитные явления не только сам принцип относительности Галилея, но и галилеево правило сложения скоростей, вытекающее из галилее-ва правила преобразования координат (см. п. 10). Следовательно, преобразования Галилея для координат и времени, а также его правило сложения скоростей к электромагнитным явлениям неприменимы. Преобразования Лоренца и инварианты этих преобразований. Основы СТО были заложены Эйнштейном. Эта теория представляет современную физическую теорию пространства и времени, в которой полагается что время однородно и изотропно. В основе СТО лежат постулаты Эйнштейна. Постулаты: 1) Принцип относительности: никакие опыты, проведенные внутри данной инерциальной системы отсчета, не дают возможности обнаружить, покоится ли эта система или движется равномерно и прямолинейно; все законы природы инвариантны по отношению к переходу от одной системы отсчета к другой. (согласно этому постулату все ИСО равноправны, то есть явления во всех системах протекают одинаково). 2) Принцип инвариантности скорости света: скорость света в вакууме не зависит от скорости движения источника света или наблюдателя и одинакова во всех ИСО. (согласно этому постулату, постоянство скорости света – фундаментальное свойство природы, которое констатируется как факт). Преобразования Лоренца. Рассмотрим две ИСО K (с координатами x,y,z) и К’ (с координатами x’,y’,z’), движущимися относительно K (вдоль оси x) со скоростью v=const. Пусть в начальный момент времени начала координат O и O’ совпадают, излучается световой импульс. Согласно второму постулату Эйнштейна скорость света в обеих системах одинакова и равна c. Поэтому если за время t в системе К сигнал дойдет до некоторой точки, пройдя расстояние x=ct, то в K’ координата светового импульса в момент движения точки A x’=ct’. Вычитая получаем x’-x=c(t’-t). Так как x=!x’, то t!=t, то есть отсчет времени в системах К и K’ различен – отсчет времени имеет относительный характер (в классической физике считается, что время во всех ИСО течет одинаково). Эйнштейн показал, что в теории относительности классические преобразования Галилея, описывающие переход от одной системы отсчета к другой, заменяются преобразованиями Лоренца, удовлетворяющими постулатам Эйнштейна. Эти преобразования были предложены Лоренцом в 1904 году, еще до появления СТО и имеют вид: 1) при К->K’. x’=(x-vt)/√(1-β²), y’=y, z’=z, t’=(t-vx/c²)/√(1-β²); 2) при К’->K x=(x’+vt’)/ √(1-β²), y=y’, z=z’, t=(t’+vx’/c²)/√(1-β²); (примечание β=v/c). Из преобразований Лоренца следует важный вывод о том, что как расстояние, таки промежуток времени между двумя событиями меняются при переходе от одной ИСО к другой. Инварианты преобразований: инварианты – величины, которые не изменяются при переходе от одной ИСО к другой. с=3*108 м/с. Интервал между двумя событиями ∆S= √(c2∆t2-∆x2-∆y2-∆z2). E=c√(p2+m02c2), (E2/c2)-p2= m02c2. (E2/c2)-p2=inv. Релятивистская динамика Энергия и импульс Если частица с массой m движется со скоростью
Эти соотношения обобщают классические выражения для энергии и импульса, получающиеся в результате разложения в ряд по
При нулевой скорости, энергия частицы называется энергией покоя: При приближении скорости тела к скорости света, его энергия и импульс стремятся к бесконечности. Это одна из причин, по которой «обычные» объекты неспособны двигаться быстрее скорости света. Для частицы с ненулевой массой даже достижение скорости света потребует затраты бесконечной энергии. Заметные отклонения от классических выражений для энергии и импульса происходят при скоростях близких к скорости света. Если скорости относительно невелики, то отклонения от классической динамики незначительны. Например, при скорости u=c/4, относительная разница релятивистского и классического импульса составляет всего 3 %. Между релятивистской энергией и импульсом существуют следующие связи:
Эти формулы остаются справедливыми и для объектов, движущихся со скоростью света. В этом случае их масса должна быть равна нулю [править]Уравнения движения Действующая на тело сила
остаётся справедливым также и в теории относительности. Однако, производная по времени берётся от релятивистского импульса, а не от классического. Это приводит к тому, что связь силы и ускорения существенно отличается от классической:
Первое слагаемое содержит «релятивистскую массу», равную отношению силы к ускорению, если сила действует перпендикулярно скорости. В ранних работах по теории относительности её называли «поперечной массой». Именно её «рост» наблюдается в экспериментах по отклонению электронов магнитным полем. Второе слагаемое содержит «продольную массу», равную отношению силы к ускорению, если сила действует параллельно скорости:
Как было отмечено выше, эти понятия являются устаревшими и связаны с попыткой сохранить классическое уравнение движения Ньютона Скорость изменения энергии равна скалярному произведению силы на скорость тела:
Это приводит к тому, что, как и в классической механике, составляющая силы перпендикулярная к скорости частицы не изменяет её энергию (например, магнитная составляющая в силе Лоренца). Уравнение неразрывности.
Хотя гидроаэродинамика основана на трёх хорошо известных в механике законах сохранения массы, импульса и энергии, формулировки этих законов в ней выглядят сложнее. Например, обычное определение закона сохранения массы гласит, что масса системы тел остаётся неизменной. Для жидкости, текущей в трубе, этот закон используется в форме, называемой уравнением неразрывности. Уравнение неразрывности - соотношение между скоростью течения, объемным расходом среды и расстоянием между линиями тока. Это уравнение выражает один из основных законов гидроаэромеханики, согласно которому объемный расход во всякой трубке тока, ограниченной соседними линиями тока, должен быть в любой момент времени одинаков во всех ее поперечных сечениях. Поскольку объемный расход Q равен произведению скорости текущей среды V на площадь A поперечного сечения трубки тока, уравнение неразрывности имеет следующий вид: Q = V 1 A 1 = V 2 A 2 или же vS = const (v – скорость жидкости, S – площадь сечения трубы, по которой течёт жидкость. Смысл – сколько воды вливается – столько и должно вылиться, если условия течения неизменны). Поэтому там, где сечение велико и линии тока разрежены, скорость должна быть мала, и наоборот. (Все три части этого двойного равенства должны выражаться в одной и той же системе единиц. Так, если величина Q выражена в м3/с, то скорость V должна выражаться в м/с, а площадь A – в м2.)
Уравнение Бернулли.
Одно из важнейших уравнений гидромеханики было получено в 1738 году швейцарским учёным Даниилом Бернулли. Ему впервые удалось описать движение несжимаемой идеальной жидкости (силы трения между элементами идеальной жидкости, а также между идеальной жидкостью и стенками сосуда отсутствуют). Уравнение Бернулли имеет вид:
р + рv2 + pgh = const. 2 где р – давление жидкости, р – её плотность, V – скорость движения, g – ускорение свободного падения, h – высота, на которой находится элемент жидкости. Согласно уравнению Бернулли, в случае установившегося течения, для которого не имеют существенного значения все другие характеристики текущей среды, кроме плотности (удельного веса), полный напор одинаков во всех поперечных сечениях трубки тока. Если к отверстию в стенке трубы присоединить манометрическую трубку, то жидкость в такой трубке поднимется на высоту, равную гидростатическому напору. Если манометрическую трубку выставить навстречу потоку, то жидкость в манометре поднимется на дополнительную высоту, равную скоростному напору. Трубка, имеющая одновременно торцевое и боковые манометрические отверстия, называется трубкой Пито и используется для определения скорости течения по измеренному скоростному напору. Трубки Пито входят в комплект измерительного оборудования всех самолетов, а также широко применяются для измерений скорости течения в трубопроводах, вентиляционных воздуховодах, в аэро- и гидродинамических трубах. Если скорость течения равна нулю (т.е. среда не движется), то уравнение Бернулли сводится к простому уравнению гидростатики. Согласно этому уравнению, увеличению высоты в неподвижной среде жидкости или газа соответствует равное уменьшение гидростатического напора. Поэтому давление в любой точке неподвижной жидкости равно глубине этой точки под свободной поверхностью, умноженной на удельный вес жидкости. На основе этого соотношения вычисляется давление жидкости на стенки резервуаров, а также проводится анализ плавучести и остойчивости морских и речных судов. В тех случаях, когда скорость течения отлична от нуля, уравнение Бернулли совместно с уравнениями неразрывности и закона сохранения количества движения позволяет решать практически важные задачи – о расходе среды, текущей через измерительные диафрагмы, поверх измерительных и водосбросных водосливов и под затворы шлюзовых галерей; о траектории струи жидкости; о форме, скорости и силе волн, действующих на суда и волноломы. Хотя в таких задачах обычно рассматривается течение воды под атмосферным слоем воздуха, аналогичные процессы гравитационного характера имеют место в случае течения более холодной (и, следовательно, более плотной) воды под более теплой, как и других жидкостей и газов разной плотности. Таким образом, водным потокам в реках аналогичны океанские течения и ветры, поскольку все гравитационные явления подчиняются одним и тем же законам гидроаэромеханики. Классификации колебаний Выделение разных видов колебаний зависит от свойства, которое хотят подчеркнуть. Для подчёркивания разной физической природы колеблющихся систем выделяют, например, колебания: ● механические (звук, вибрация); ● электромагнитные (свет, радиоволны, тепловые); ● комбинации вышеперечисленных; По характеру взаимодействия с окружающей средой: ● вынужденные – колебания, протекающие в системе под влиянием внешнего периодического воздействия; ● собственные или свободные – колебания при отсутствии внешних сил, когда система, после первоначального воздействия внешней силы, предоставляется самой себе (в реальных условиях свободные колебания всегда затухающие); ● автоколебания – колебания, при которых система имеет запас потенциальной энергии и она расходуется на совершение колебаний (пример такой системы - механические часы). Характеристики колебательного движения: Смещение х - отклонение колеблющейся точки от положения равновесия в данный момент времени (м). Амплитуда А – максимальное отклонение тела от положения равновесия. Если колебания незатухающие, то амплитуда постоянна (м). Период Т — время, за которое совершается одно полное колебание. Выражается в секундах (с). Фаза колебания - физическая величина, определяющая смещение x в данный момент времени. Измеряется в радианах (рад). Фаза колебания в начальный момент времени (t=0) называется начальной фазой.
Частота — число полных колебаний за единицу времени. В СИ измеряется в герцах (Гц)
Циклическая частота колебаний ω – это число полных колебаний, происходящих за 2π секунд. Единица циклической частоты – радиан в секунду (рад/с).
Волновое уравнение. Распространение волн в однородной изотропной среде в общем случае описывается волновым уравнением - дифференциальным уравнением в частных производных.
Решением уравнения (4) является уравнение любой волны (плоской, сферической и т.д.). В частности, для анализируемой здесь плоской гармонической волны (1), которая не зависит от координат y и z волновое уравнение принимает вид Cоответствующей подстановкой можно убедится, что уравнению (6) удовлетворяет уравнение (1).
Энергия бегущей волны. Вектор плотности потока энергии Упругая среда, в которой распространяется волна, обладает как кинетической энергией колебательного движения частиц так и потенциальной энергией, обусловленной деформацией среды. Можно показать, что объемная плотность энергии для плоской бегущей гармонической волны S=Acos(ω(t-
где r=dm/dV - плотность среды, т.е. периодически изменяется от 0 до rА2w2 за время p/w=Т/2. Среднее значение плотности энергии за промежуток времени p/w=Т/2
Для характеристики переноса энергии вводят понятие вектора плотности потока энергии
где DV=DS^ uDt - объем элементарного цилиндра, выделенного в среде. Поскольку скорость переноса энергии или групповая скорость есть вектор, то и плотность потока энергии можно представить в виде вектора Когда говорят о интенсивности, то подразумевают физическое значение вектора –потока энергии. Интенсивность волны пропорциональна квадрату амплитуды. Вектор Умова.
|
||||||||||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 1257; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.137.64 (0.124 с.) |
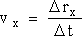 , отсюда получаем уравнение равномерного движения:
, отсюда получаем уравнение равномерного движения: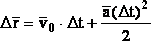
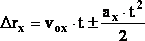
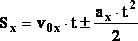
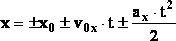
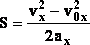
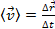 . Мгновенная скорость мат точки – средняя скорость за бесконечно малый инт вр, определяемая как векторная величина, равная первой производной по вр от радиус-вектора
. Мгновенная скорость мат точки – средняя скорость за бесконечно малый инт вр, определяемая как векторная величина, равная первой производной по вр от радиус-вектора  рассматриваемой точки:
рассматриваемой точки: 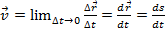 . Вектор мгновенной скорости напрвлен по касательной к траектории в сторону движения. В неравномерном движении модуль мгновенной скорости с течением времени изменяется
. Вектор мгновенной скорости напрвлен по касательной к траектории в сторону движения. В неравномерном движении модуль мгновенной скорости с течением времени изменяется 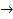 средняя скорость неравномерного движения (средняя путевая скорость) – пройденное телом расстояние s, деленное на время, затраченное на прохождение этого расстояния:
средняя скорость неравномерного движения (средняя путевая скорость) – пройденное телом расстояние s, деленное на время, затраченное на прохождение этого расстояния: 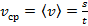 .
. 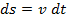 ->
-> 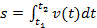 . Равномерное движение – точка за любые равные промеж вр проходит равные расстояния. Ускорение – векторная величина, определяемая как изменение скорости в ед вр:
. Равномерное движение – точка за любые равные промеж вр проходит равные расстояния. Ускорение – векторная величина, определяемая как изменение скорости в ед вр: 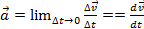 . Кинематический закон изменения скорости:
. Кинематический закон изменения скорости: 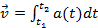 .
. .
.  – геометрическая сумма всех сил, действующих на данное тело со стороныдругих тел,
– геометрическая сумма всех сил, действующих на данное тело со стороныдругих тел,  – сумма сил инерции, действующих на тело.
– сумма сил инерции, действующих на тело. ,
,  – сила натяжения нити,
– сила натяжения нити,  – равнодействующая силы тяжести и силы натяжения нити.
– равнодействующая силы тяжести и силы натяжения нити. 2). В СО, вращающейся с постоянной
2). В СО, вращающейся с постоянной  , на покоящееся в ней тело действует центробежная сила инерции
, на покоящееся в ней тело действует центробежная сила инерции  :
:  . Переносное ускорение при этом:
. Переносное ускорение при этом:  .
. относительно неподвижной ИСО, то переносное ускорение
относительно неподвижной ИСО, то переносное ускорение  . Действуют 3 силы: 1. поступательная сила инерции
. Действуют 3 силы: 1. поступательная сила инерции  . Возникает при поступательном движении НИСО. 2. Центробежная сила инерции
. Возникает при поступательном движении НИСО. 2. Центробежная сила инерции  .Действует во вращающихся СО и на движущиеся, и на неподвижные тела, удаленные от оси вращения на конечное расстояние r. 3. кориолисова сила инерции
.Действует во вращающихся СО и на движущиеся, и на неподвижные тела, удаленные от оси вращения на конечное расстояние r. 3. кориолисова сила инерции  . Действует во вращающейся системе координат только на движущиеся с относительной скоростью
. Действует во вращающейся системе координат только на движущиеся с относительной скоростью  тела. Когда скорость эт движения =0, эта сила исчезает. Она зависит от угловой скорости вращения и относительной скорости вращения. Т.о.
тела. Когда скорость эт движения =0, эта сила исчезает. Она зависит от угловой скорости вращения и относительной скорости вращения. Т.о.  ,
,  – сумма сил, действующих на тело со стороны других тел.
– сумма сил, действующих на тело со стороны других тел. , где
, где  — кориолисово ускорение. Соответственно, тело действует по третьему закону Ньютона с силой противоположной направленности.
— кориолисово ускорение. Соответственно, тело действует по третьему закону Ньютона с силой противоположной направленности.  Сила, которая действует со стороны тела, и будет называться силой Кориолиса. Не следует путать Кориолисову силу с другой силой инерции — центробежной силой, которая направлена по радиусу вращающейся окружности.
Сила, которая действует со стороны тела, и будет называться силой Кориолиса. Не следует путать Кориолисову силу с другой силой инерции — центробежной силой, которая направлена по радиусу вращающейся окружности.


 .
. , и можно записать
, и можно записать 



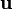 , то её энергия и импульс имеют следующую зависимость от скорости:
, то её энергия и импульс имеют следующую зависимость от скорости:
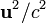 :
: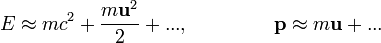
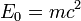 . В современной физической литературе, принято, что m — масса частицы не зависит от скорости, являясь инвариантом относительно преобразований Лоренца, и является величиной неаддитивной. Понятие «релятивистской массы», зависящей от скорости
. В современной физической литературе, принято, что m — масса частицы не зависит от скорости, являясь инвариантом относительно преобразований Лоренца, и является величиной неаддитивной. Понятие «релятивистской массы», зависящей от скорости 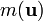 не используется [25], хотя оно и встречается в ранних работах по теории относительности. Историческая причина введения этого понятия была связана с попытками сохранить для релятивистского импульса классическую форму:
не используется [25], хотя оно и встречается в ранних работах по теории относительности. Историческая причина введения этого понятия была связана с попытками сохранить для релятивистского импульса классическую форму: 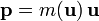 .
.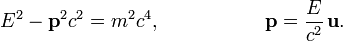
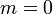 .
.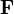 изменяет его импульс. Поэтому второй закон Ньютона в форме
изменяет его импульс. Поэтому второй закон Ньютона в форме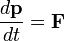
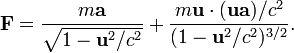
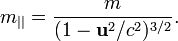
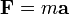 .
.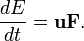
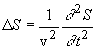 , (4) где
, (4) где 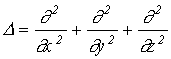 (5)-оператор Лапласа, v - фазовая скорость.
(5)-оператор Лапласа, v - фазовая скорость.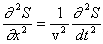 . (6)
. (6) )+φ0)
)+φ0)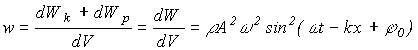 (14)
(14)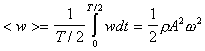 . (16)
. (16)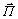 - вектор Умова. Выведем выражение для него. Если через площадку DS^, перпендикулярную к направлению распространения волны, переносится за время Dt энергия DW, то плотность потока энергии Рис. 2
- вектор Умова. Выведем выражение для него. Если через площадку DS^, перпендикулярную к направлению распространения волны, переносится за время Dt энергия DW, то плотность потока энергии Рис. 2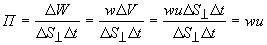 , (17)
, (17) 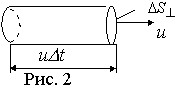
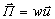 , Вт/м2 (18) Этот вектор ввел профессор Московского университета Н.А. Умов в 1874 г. Среднее значение его модуля называют интенсивностью волны
, Вт/м2 (18) Этот вектор ввел профессор Московского университета Н.А. Умов в 1874 г. Среднее значение его модуля называют интенсивностью волны 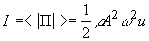 (19) Для гармонической волны u=v [cм.(14)], поэтому для такой волны в формулах (17)-(19) u можно заменить на v. Интенсивность определяется плотностью потока энергий – этовектор совпадает с направлением, в котором переносится энергия и равен потоку энергии перенсимой через……………..
(19) Для гармонической волны u=v [cм.(14)], поэтому для такой волны в формулах (17)-(19) u можно заменить на v. Интенсивность определяется плотностью потока энергий – этовектор совпадает с направлением, в котором переносится энергия и равен потоку энергии перенсимой через……………..


