
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Свойства линейного дифференциального оператора
1) Постоянный множитель можно выносить за знак линейного дифференциального оператора, то есть 2) Линейный дифференциальный оператор от суммы функций равен сумме линейных дифференциальных операторов от слагаемых, то есть
При доказательстве этих свойств пользуемся соответствующими свойствами производной. Например, докажем первое свойство: ►
Общие свойства линейных дифференциальных уравнений Отметим следующие два свойства ЛДУ: инвариантность ЛДУ относительно произвольной замены независимой переменной и относительно линейной замены искомой функции. 1. Линейное уравнение остается линейным при любой замене независимой переменной. ► Положим
Чтобы в уравнении (1) заменить независимую переменную Находим
Вторая производная от
Заменяя в уравнении (1) Если удастся найти общее решение преобразованного уравнения, то заменяя в нем 2. Линейное уравнение остается линейным при любой линейной замене искомой функции по формуле ► Используя формулу Лейбница для производных высших порядков от произведения функций, запишем, каким выражением будут заменяться производные
Замечаем, что
Линейные однородные дифференциальные уравнения С переменными коэффициентами
О решениях ЛОДУ Теорема 1. Если
также является решением уравнения (1). ► Рассмотрим Так как Пусть мы нашли Убедимся в том, что решение, составленное из любых не всегда будет общим. Например, если возьмем случае примет вид льная постоянная, которая может быть обозначена просто через
Условие линейной независимости (зависимости) системы функций. Определение. Система функций Пример. 1. Функции 2. Функции
не может выполняться тождественно, когда не все Система из двух функций
если же
то система функций линейно независимая на отрезке
Определение. Определителем Вронского, составленным для функций
Теорема 2. Для того, чтобы система функций
|
||||||
|
Последнее изменение этой страницы: 2016-09-18; просмотров: 819; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.220.1.239 (0.015 с.) |
 .
. .
. . ◄
. ◄ , где
, где  – произвольная функция от
– произвольная функция от  , непрерывно-дифференцируемая на
, непрерывно-дифференцируемая на 
 раз, производная которой
раз, производная которой  на
на  . Эти условия будут обеспечивать существование обратной функции
. Эти условия будут обеспечивать существование обратной функции  и ее производной
и ее производной .
. другой независимой переменной
другой независимой переменной  по
по 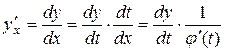 ,
,
 .
. -го порядка
-го порядка  выразится в виде линейной и однородной функции, зависящей от
выразится в виде линейной и однородной функции, зависящей от .
. , а производные от
, а производные от  , получим уравнение
, получим уравнение  , мы получим решение исходного уравнения. ◄
, мы получим решение исходного уравнения. ◄ , где
, где  – произвольная функция,
– произвольная функция,  – новая искомая функция.
– новая искомая функция. .
.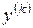 является линейной однородной функцией относительно
является линейной однородной функцией относительно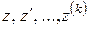 . Поэтому, заменяя функцию и ее производные по соответствующим формулам, получим линейное уравнение
. Поэтому, заменяя функцию и ее производные по соответствующим формулам, получим линейное уравнение 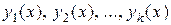 – решения ЛОДУ (1), то любая линейная комбинация этих решений с произвольными постоянными
– решения ЛОДУ (1), то любая линейная комбинация этих решений с произвольными постоянными ,
, .
. , то
, то  , а поэтому
, а поэтому  – решение уравнения (1). ◄
– решение уравнения (1). ◄ ЛОДУ
ЛОДУ  -го порядка. Тогда по теореме 1
-го порядка. Тогда по теореме 1  (2), где
(2), где  – произвольные постоянные, также есть решение уравнения (1). Известно, что общее решение уравнения
– произвольные постоянные, также есть решение уравнения (1). Известно, что общее решение уравнения  , составленное из любых
, составленное из любых  , то функция (2) в этом
, то функция (2) в этом . Так как
. Так как  есть произво-
есть произво- , то функция будет содержать
, то функция будет содержать  произвольных постоянных и поэтому не является общим решением. Ясно, что функция (2) не всегда дает общее решение. Возникает вопрос, какими функциями должны быть частные решения, чтобы формула (2) давала общее решение. Этот вопрос разрешается в связи с понятием линейной зависимости функций.
произвольных постоянных и поэтому не является общим решением. Ясно, что функция (2) не всегда дает общее решение. Возникает вопрос, какими функциями должны быть частные решения, чтобы формула (2) давала общее решение. Этот вопрос разрешается в связи с понятием линейной зависимости функций. , если существуют
, если существуют 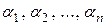 НЕРОН, такие, что имеет место тождество
НЕРОН, такие, что имеет место тождество 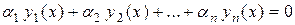 на отрезке
на отрезке 

 линейно зависимы на
линейно зависимы на  . Действительно, существуют постоянные
. Действительно, существуют постоянные  такие, что имеет место тождество
такие, что имеет место тождество 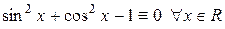 .
. линейно независимы на
линейно независимы на  , так как условие
, так как условие
 . Действительно, это равенство есть алгебраическое уравнение, оно может быть справедливо не более как для
. Действительно, это равенство есть алгебраическое уравнение, оно может быть справедливо не более как для  , является линейно зависимой, если
, является линейно зависимой, если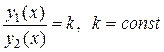 ,
, на
на 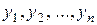 на отрезке
на отрезке  .
. .
.


