
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Статистические показатели выборочной совокупности.
Графики вариационных рядов (гистограммы) - это как бы «сгущение исходного материала», его наглядная картина. Но для сравнения разных выборок нужны количественные показатели. Существует два таких показателя (на самом деле две группы), но для простоты мы рассмотрим только основные. Вариационные ряды (выборки) могут различаться: ¨ по значению признака, вокруг которого концентрируется большинство вариант, то есть среднее арифметическое; ¨ по степени отклонения от среднего показателя, то есть вариационный размах, среднеквадратичное отклонение, или дисперсия. Остановимся подробнее на обсуждении этих величин. Среднее арифметическое
О величине среднего арифметического уже много было сказано в предыдущих главах. Что нового можно добавить с точки зрения биологической статистики? Среднее арифметическое является обобщающей величиной, которая как бы впитывает в себя все особенности данной совокупности или ряда. Величина Математическое ожидание В биологических исследованиях может представлять известный интерес среднее геометрическое:
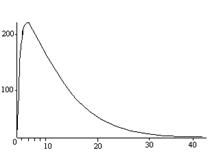
Пример. Пусть, например, необходимо вычислить средний за год ежемесячный темп прибавки веса грудного ребенка по результатам измерения относительного увеличения веса за каждый месяц. · за 1-й месяц - в 1,23 раза; · за 2-й месяц - в 1,19 раза; · за 3-й месяц - в 1,2 раза и т.д. В этом случае более адекватным выражением среднемесячного темпа привеса будет не среднее арифметическое, а среднее геометрическое значение. Для характеристики абсолютного увеличения веса более адекватным будет среднее арифметическое. Мода -это еще одна характеристика положения распределения. В тех выборочных совокупностях, где может быть произведена только классификация вариант по какому-нибудь качественному признаку, наиболее типичную группу, в которую входит больше всего вариант, называют модой. Можно использовать эту характеристику и для количественных оценок. На рисунке изображено распределение по возрасту заболевших дифтерией. Очевидно, что знание среднего возраста заболевших менее интересно, чем знание возраста, в котором чаще всего происходит заболевание (от 2 до 4 лет). В частности, при решении вопроса о том, где должны быть сосредоточены главные профилактические усилия: в школах или в дошкольных учреждениях.
Если же распределение более или менее симметрично, то мода и среднее арифметическое значение близки друг к другу. Дисперсия Однако, знания только среднего арифметического еще недостаточно для характеристики совокупности, так как главной особенностью совокупности является наличие разнообразия между ее членами, то есть вариации. Характеристикой вариации является средний квадрат отклонений Для генеральной совокупности
а среднеквадратичное отклонение s, соответственно:
Для выборочной совокупности формулы отличаются. Обратите внимание, в знаменателе вместо
Чем объяснить такое различие формул? Для ответа на этот вопрос нужно познакомиться с таким понятием как число степеней свободы. Числом степеней свободы называется число независимых переменных (вариант) минус число наложенных связей (ограничений). Число степеней свободы принято обозначать либо df (degrees of freedom), либо n (греческая буква ню). Если изучаемая совокупность состоит из трех вариант, то при расчете среднего арифметического А теперь рассмотрим ситуацию, когда по какой-то причине эти три числа (варианты) должны быть такими, чтобы их сумма была равна заданному числу, например, 300. Тогда из исходных трех вариант только 2 могут быть любыми по величине. Что же до третьей варианты, она выбирается равной
|
||||||
|
Последнее изменение этой страницы: 2016-09-18; просмотров: 584; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.117.109 (0.005 с.) |
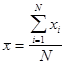 .
. дает сводную обощенную характеристику данного изучаемого признака.
дает сводную обощенную характеристику данного изучаемого признака. - есть характеристика генеральной совокупности (
- есть характеристика генеральной совокупности (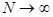 ), то есть то значение случайной величины, которое близко к истинному. Выборочное значение
), то есть то значение случайной величины, которое близко к истинному. Выборочное значение 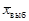 , то есть полученное по результатам выборки не равно математическому ожиданию, но чем больше объем выборки (
, то есть полученное по результатам выборки не равно математическому ожиданию, но чем больше объем выборки ( ), тем меньше отклонение
), тем меньше отклонение 
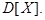
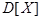 (или дисперсия),
(или дисперсия),  .
.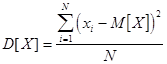 ,
,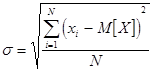 .
.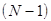 , вместо математического ожидания
, вместо математического ожидания 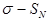 (оценка среднеквадратичного отклонения для выборки).
(оценка среднеквадратичного отклонения для выборки).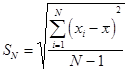
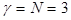 , так как никаких ограничений в данной ситуации не налагается.
, так как никаких ограничений в данной ситуации не налагается. . То есть в данном опыте накладывается одно ограничение и число степеней свободы будет
. То есть в данном опыте накладывается одно ограничение и число степеней свободы будет 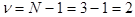 . С похожим ограничением мы сталкиваемся при расчете дисперсии или среднеквадратичного отклонения, когда подсчитывается сумма квадратов отклонений от среднего арифметического
. С похожим ограничением мы сталкиваемся при расчете дисперсии или среднеквадратичного отклонения, когда подсчитывается сумма квадратов отклонений от среднего арифметического 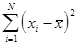 . Фиксированное значение
. Фиксированное значение 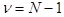 вместо
вместо 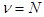 .
.


