Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Кинематика материальной точки. Основные характеристики движения. Нормальное и тангенциальное ускорения.Стр 1 из 6Следующая ⇒
Кинематика материальной точки. Основные характеристики движения. Нормальное и тангенциальное ускорения. Кинематика точки — раздел кинематики, изучающий математическое описание движения материальных точек. Основной задачей кинематики является описание движения при помощи математического аппарата без выяснения причин, вызывающих это движение. Движение любого объекта в кинематике изучают по отношению к некоторой системеотсчета, включающей: тело отсчета, систему измерения положения тела в пространстве (систему координат) и Прибор для измерения времени (Часы). Положение точки определяется набором обобщенныхкоординат — упорядоченным набором числовых величин, полностью описывающих положение тела. В самом простом случае это координаты точки (радиус-вектора) в выбранной системе координат. Материальная точка – это тело, размерами которого в условиях данной задачи можно пренебречь. Является ли тело материальной точкой, зависит не от размеров тела, а от условий задачи. Движением в механике называется изменение взаимного расположения тел. Движение происходит как в пространстве, так и во времени, поэтому для описания движения необходимо также определять время. Совокупность неподвижных друг относительно друга тел, по отношении к которым рассматривается движение, и отсчитывающего время устройства называется системой отсчёта. Всякое движение твёрдого тела можно разложить на 2 вида: поступательное и вращательное. Поступательным называется движение, при котором любая прямая, связанная с движущимся телом, остаётся параллельной самой себе. При вращательном движении все точки тела движутся по окружностям, центры которых лежат на одной прямой, называемой осью вращения. Ось вращения может быть и вне тела. Для того чтобы иметь возможность описывать движение количественно систему отсчёта связывают с системой координат. Материальная точка при своём движении описывает некоторую линию, называемую траекторией. В зависимости от формы траектории различают прямолинейное, криволинейное и движение по окружности. Радиус-вектор — вектор, определяющий положение материальной точки в пространстве. Геометрически изображается вектором, проведенным из начала координат к материальной точке. Зависимость радиус-вектора от времени
Траектория – это воображаемая линия, описываемая концом радиус-вектора в процессе движения. Иными словами, траектория — это линия вдоль которой движется материальная точка. При этом закон движения выступает как уравнение, задающее траекторию параметрически. Длину участка траектории между начальным и конечным моментами времени часто называют пройденным расстоянием или длиной пути и обозначают буквой S. При таком описании движения S выступает в качестве обобщенной координаты, а законы движения в этом случае записывается в виде Момент силы, действующей на материальную точку, относительно оси вращения. а) Пусть материальная точка массы m вращается относительно оси ОО ΄. Обозначим r - радиус-вектор, проведенный от оси вращения до точки приложения силы F (Рисунок 10).
Рисунок 10. Вращение материальной точки Моментом силы F относительно оси вращения называется вектор M, равный векторному произведению радиус-вектора на вектор силы M = [ r∙ F] и направленный по оси вращения в сторону, определяемую по правилу правого буравчика Модуль вектора момента силы равен M = F ∙ r ∙ sinα, где α - угол между векторами r и F. Момент импульса. Моментом импульса материальной точки относительно оси вращения называется вектор L, равный векторному произведению радиуса-вектора r на вектор импульса P: L = [ r∙P] = [ r∙ m v ], где m, v - соответственно масса и вектор скорости точки. Направление L определяется по правилу правого буравчика. Модуль вектора L = mv∙ r∙ sinα, где α - угол между векторами r и v. Законы сохранения. Законы сохранения — фундаментальные физические законы, согласно которым при определённых условиях некоторые измеримые физические величины, характеризующие замкнутую физическую систему, не изменяются с течением времени. Закон сохранения энергии — фундаментальный закон природы, установленный эмпирически и заключающийся в том, что энергия изолированной (замкнутой) физической системы сохраняется с течением времени. Другими словами, энергия не может возникнуть из ничего и не может исчезнуть в никуда, она может только переходить из одной формы в другую.
Закон сохранения импульса (Закон сохранения количества движения) утверждает, что сумма импульсов всех тел (или частиц) замкнутой системы есть величина постоянная. Из законов Ньютона можно показать, что при движении в пустом пространстве импульс сохраняется во времени, а при наличии взаимодействия скорость его изменения определяется суммой приложенных сил. В классической механике закон сохранения импульса обычно выводится как следствие законов Ньютона. Закон сохранения момента импульса (закон сохранения углового момента) — векторная сумма всех моментов импульса относительно любой оси для замкнутой системы остается постоянной в случае равновесия системы. В соответствии с этим, момент импульса замкнутой системы относительно любой неподвижной точки не изменяется со временем. Условие плавания тел Поведение тела, находящегося в жидкости или газе, зависит от соотношения между модулями силы тяжести
Другая формулировка (где · · · Уравнение Бернулли. Закон Бернулли является следствием закона сохранения энергии для стационарного потока идеальной (то есть без внутреннего трения) несжимаемой жидкости: Согласно закону Бернулли полное давление в установившемся потоке жидкости остается постоянным вдоль этого потока. Полное давление состоит из весового (ρ gh), статического (p) и динамического Из закона Бернулли следует, что при уменьшении сечения потока, из-за возрастания скорости, то есть динамического давления, статическое давление падает. Закон Бернулли справедлив в чистом виде только для жидкостей, вязкость которых равна нулю, то есть таких жидкостей, которые не прилипают к поверхности трубы. На самом деле экспериментально установлено, что скорость жидкости на поверхности твердого тела почти всегда в точности равна нулю (кроме случаев отрыва струй при некоторых редких условиях). Закон Бернулли можно применить к истечению идеальной несжимаемой жидкости через малое отверстие в боковой стенке или дне широкого сосуда. Для сжимаемого идеального газа
Силы вязкого трения. В предыдущих лекциях мы рассматривали движение жидкости и газа в пренебрежении силами вязкого трения. Между тем, эти силы, действующие между частицами движущейся жидкости, могут кардинальным образом повлиять как на распределение скоростей в потоке жидкости, так и на обтекание жидкостью тел, помещенных в движущийся поток.
Волны. Уравнение волны. Волна — изменение состояния среды (возмущение), распространяющееся в этой среде и переносящее с собой энергию. Другими словами: «…волнами или волной называют изменяющееся со временем пространственное чередование максимумов и минимумов любой физической величины, например, плотности вещества, напряжённости электрического поля, температуры». Перенос энергии — принципиальное отличие волн от колебаний, в которых происходят лишь «местные» преобразования энергии. Волны же, как правило, способны удаляться на значительные расстояния от места своего возникновения (по этой причине волны иногда называют «колебанием, оторвавшимся от излучателя»). Математическое описание волн основывается на представлении о них, как о пространственно распространяющихся колебаниях, и в общем виде записывается:
где u — отклонение от некоего среднего положения в точке r во время t. Более определённый вид уравнения зависит от типа волны. Гармоническая волна Изменение колеблющейся величины u для гармонически распространяющейся волны в начале координат описывается формулой:
где A — амплитуда, t — время, а T — период волны. В любой другой точке, расположенной на расстоянии r от начала координат в направлении распространения волны, изменение u происходит с опозданием на время t 1:
Уравнением волны называется выражение, которое дает смещение колеблющейся точки как функцию ее координат (x, y, z) и времени t. Эта функция должна быть периодической как относительно времени, так и координат (волна – это распространяющееся колебание, следовательно периодически повторяющееся движение). Кроме того, точки, отстоящие друг от друга на расстоянии l, колеблются одинаковым образом. Уравнение плоской волны Найдем вид функции x в случае плоской волны, предполагая, что колебания носят гармонический характер. Направим оси координат так, чтобы ось x совпадала с направлением распространения волны. Тогда волновая поверхность будет перпендикулярна оси x. Так как все точки волновой поверхности колеблются одинаково, смещение x будет зависеть только от х и t:
Найдем вид колебания частиц в плоскости, соответствующей произвольному значению x. Чтобы пройти путь x, необходимо время Следовательно, колебания частиц в плоскости x будут отставать по времени на t от колебаний частиц в плоскости
– это уравнение плоской волны. Таким образом, x есть смещение любой из точек с координатой x в момент времени t. При выводе мы предполагали, что амплитуда колебания Такой же вид уравнение (5.2.3) будет иметь, если колебания распространяются вдоль оси y или z. В общем виде уравнение плоской волны записывается так:
Выражения (5.2.3) и (5.2.4) есть уравнения бегущей волны. Уравнение (5.2.3) описывает волну, распространяющуюся в сторону увеличения x. Волна, распространяющаяся в противоположном направлении, имеет вид:
Уравнение волны можно записать и в другом виде. Введем волновое число
где Так как
Уравнение сферической волны В случае, когда скорость волны υ во всех направлениях постоянна, а источник точечный, волна будет сферической. Предположим, что фаза колебаний источника равна w t (т.е.
где А равна амплитуде на расстоянии от источника равном единице. Уравнение (5.2.7) неприменимо для малых r, т.к. при Бегущими волнами называются волны, которые переносят в пространстве энергию. Перенос энергии в волнах количественно характеризуется вектором плотности потока энергии. Этот вектор для упругих волн называется вектором Умова (по имени русского ученого Н. А. Умова (1846— 1915), решившего задачу о движении энергии в среде). Направление вектора Умова совпадает с направлением переноса энергии, а его модуль равен энергии, переносимой волной за единицу времени через единичную площадку, расположенную перпендикулярно направлению распространения волны. Для вывода уравнения бегущей волны — зависимости смещения колеблющейся частицы от координат и времени — рассмотрим плоскую волну, предполагая, что колебания носят гармонический характер, а ось х совпадает с направлением распространения волны (рис. 220). В данном случае волновые поверхности перпендикулярны оси х, а так как все точки волновой поверхности колеблются одинаково, то смещение x будет зависеть только от х и t, т. е. x=x (х, t). На рис. 220 рассмотрим некоторую частицу среды В, находящуюся от источника колебаний О на расстоянии х. Если колебания точек, лежащих в плоскости х= 0, описываются функцией x(0, t)=А coswt, то частица среды В колеблется по тому же закону, но ее колебания будут отставать по времени от колебаний источника на т, так как для прохождения волной расстояния х требуется время t= x/v, где v — скорость распространения волны. Тогда уравнение колебаний частиц, лежащих в плоскости х, имеет вид x(x,t)=Acosw(t-x/v), (154.1) откуда следует, что x (х, t) является не только периодической функцией времени, но и периодической функцией координаты х. Уравнение (154.1) есть уравнение бегущей волны. Если плоская волна распространяется в противоположном направлении, то x(х, t)=A cosw(t+x/v). В общем случае уравнение плоской волны, распространяющейся вдоль положительного направления оси х в среде, не поглощающей энергию, имеет вид x(x,t)=Acos[w(t -х/v)+j0], (154.2) где А= const — амплитуда волны, w — циклическая частота волны, j0 — начальная фаза колебаний, определяемая в общем случае выбором начал отсчета х и t, [w (t-x /v)+j0]— фаза плоской волны. Для характеристики волн используется волновое число k=2p/l=2p/vT=w/v. (154.3) Учитывая (154.3), уравнению (154.2) можно придать вид x(x,t)=A cos(wt-kх+j0). (154.4) Уравнение волны, распространяющейся вдоль отрицательного направления оси х, отличается от (154.4) только знаком члена kx. Основываясь на формуле Эйлера (140.7), уравнение плоской волны можно записать в виде x(x,t)=Aei(wt-kx+j0), где физический смысл имеет лишь действительная часть. Предположим, что при волновом процессе фаза постоянна, т. е. w(t-x/v)+j0=const. (154.5) Продифференцировав выражение (154.5) и сократив на w, получим dt -(1/v) dx=0, откуда dx/dt=v. Следовательно, скорость v распространения волны в уравнении есть не что иное, как скорость перемещения фазы волны, и ее называют фазовой скоростью. Повторяя ход рассуждений для плоской волны, можно доказать, что уравнение сферической волны — волны, волновые поверхности которой имеют вид концентрических сфер, записывается как x(r,t)=A0/rcos(wt-kr+j0), (154.7) где r — расстояние от центра волны до рассматриваемой точки среды. В случае сферической волны даже в среде, не поглощающей энергию, амплитуда колебаний не остается постоянной, а убывает с расстоянием по закону 1 /r. Уравнение (154.7) справедливо лишь для r, значительно превышающих размеры источника (тогда источник колебаний можно считать точечным). Из выражения (154.3) вытекает, что фазовая скорость v=w/k. (154.8) Если фазовая скорость волн в среде зависит от их частоты, то это явление называют дисперсией волн, а среда, в которой наблюдается дисперсия волн, называется диспергирующей средой. Распространение волн в однородной изотропной среде в общем случае описывается волновым уравнением — дифференциальным уравнением в частных производных
где v — фазовая скорость, D= д 2/ д x2 + д 2/ д y2 + д 2/ д z2 — оператор Лапласа. Решением уравнения (154.9) является уравнение любой волны. Соответствующей подстановкой можно убедиться, что уравнению (154.9) удовлетворяют, в частности, плоская волна (см. (154.2)) и сферическая волна (см. (154.7)). Для плоской волны, распространяющейся вдоль оси х, волновое уравнение имеет вид
Кинематика материальной точки. Основные характеристики движения. Нормальное и тангенциальное ускорения. Кинематика точки — раздел кинематики, изучающий математическое описание движения материальных точек. Основной задачей кинематики является описание движения при помощи математического аппарата без выяснения причин, вызывающих это движение. Движение любого объекта в кинематике изучают по отношению к некоторой системеотсчета, включающей: тело отсчета, систему измерения положения тела в пространстве (систему координат) и Прибор для измерения времени (Часы). Положение точки определяется набором обобщенныхкоординат — упорядоченным набором числовых величин, полностью описывающих положение тела. В самом простом случае это координаты точки (радиус-вектора) в выбранной системе координат. Материальная точка – это тело, размерами которого в условиях данной задачи можно пренебречь. Является ли тело материальной точкой, зависит не от размеров тела, а от условий задачи. Движением в механике называется изменение взаимного расположения тел. Движение происходит как в пространстве, так и во времени, поэтому для описания движения необходимо также определять время. Совокупность неподвижных друг относительно друга тел, по отношении к которым рассматривается движение, и отсчитывающего время устройства называется системой отсчёта. Всякое движение твёрдого тела можно разложить на 2 вида: поступательное и вращательное. Поступательным называется движение, при котором любая прямая, связанная с движущимся телом, остаётся параллельной самой себе. При вращательном движении все точки тела движутся по окружностям, центры которых лежат на одной прямой, называемой осью вращения. Ось вращения может быть и вне тела. Для того чтобы иметь возможность описывать движение количественно систему отсчёта связывают с системой координат. Материальная точка при своём движении описывает некоторую линию, называемую траекторией. В зависимости от формы траектории различают прямолинейное, криволинейное и движение по окружности. Радиус-вектор — вектор, определяющий положение материальной точки в пространстве. Геометрически изображается вектором, проведенным из начала координат к материальной точке. Зависимость радиус-вектора от времени Траектория – это воображаемая линия, описываемая концом радиус-вектора в процессе движения. Иными словами, траектория — это линия вдоль которой движется материальная точка. При этом закон движения выступает как уравнение, задающее траекторию параметрически. Длину участка траектории между начальным и конечным моментами времени часто называют пройденным расстоянием или длиной пути и обозначают буквой S. При таком описании движения S выступает в качестве обобщенной координаты, а законы движения в этом случае записывается в виде
|
|||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-13; просмотров: 443; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.136.97.64 (0.072 с.) |
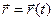 называется законом движения.
называется законом движения.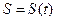 и аналогичны соответствующим законам для координат. Например закон равноускоренного криволинейного движения может быть записан в виде:
и аналогичны соответствующим законам для координат. Например закон равноускоренного криволинейного движения может быть записан в виде: 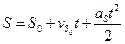 , где
, где 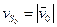 – модуль начальной скорости, а
– модуль начальной скорости, а  о – тангенциальное ускорение.
о – тангенциальное ускорение.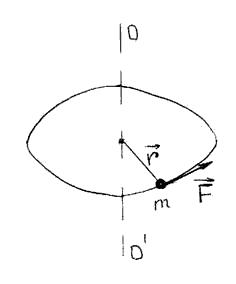
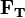 и силы Архимеда
и силы Архимеда  , которые действуют на это тело. Возможны следующие три случая:
, которые действуют на это тело. Возможны следующие три случая: — тело тонет;
— тело тонет;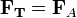 — тело плавает в жидкости или газе;
— тело плавает в жидкости или газе; — тело всплывает до тех пор, пока не начнет плавать.
— тело всплывает до тех пор, пока не начнет плавать.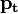 — плотность тела,
— плотность тела, 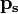 — плотность среды, в которую оно погружено):
— плотность среды, в которую оно погружено):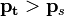 — тело тонет;
— тело тонет; — тело плавает в жидкости или газе;
— тело плавает в жидкости или газе;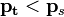 — тело всплывает до тех пор, пока не начнет плавать.
— тело всплывает до тех пор, пока не начнет плавать.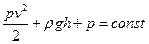 , здесь
, здесь 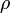 — плотность жидкости,
— плотность жидкости, 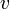 — скорость потока,
— скорость потока, 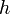 — высота, на которой находится рассматриваемый элемент жидкости,
— высота, на которой находится рассматриваемый элемент жидкости, 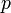 — давление в точке пространства, где расположен центр массы рассматриваемого элемента жидкости,
— давление в точке пространства, где расположен центр массы рассматриваемого элемента жидкости, 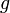 — ускорение свободного падения. Константа в правой части обычно называется напором, или полным давлением, а также интегралом Бернулли. Размерность всех слагаемых — единица энергии, приходящейся на единицу объёма жидкости.
— ускорение свободного падения. Константа в правой части обычно называется напором, или полным давлением, а также интегралом Бернулли. Размерность всех слагаемых — единица энергии, приходящейся на единицу объёма жидкости.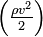 давлений.
давлений.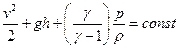 , (постоянна вдоль линии тока или линии вихря) где
, (постоянна вдоль линии тока или линии вихря) где 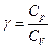 — Адиабатическая постоянная газа, p — давление газа в точке, ρ — плотность газа в точке, v — скорость течения газа, g — ускорение свободного падения, h — высота относительно начала координат. При движении в неоднородном поле gh заменяется на потенциал гравитационного поля.
— Адиабатическая постоянная газа, p — давление газа в точке, ρ — плотность газа в точке, v — скорость течения газа, g — ускорение свободного падения, h — высота относительно начала координат. При движении в неоднородном поле gh заменяется на потенциал гравитационного поля.
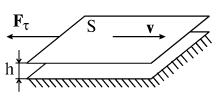
 .
.
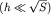 . Важно отметить, что частицы жидкости, прилегающие к верхней пластине, движутся вместе с нею со скоростью v (увлекаются пластиной). Напротив, частицы жидкости вблизи нижней (неподвижной) пластины находятся в покое (прилипают к пластине). Если мысленно разбить жидкость на параллельные плоские слои, движущиеся равномерно, то нетрудно понять, что каждый вышележащий слой увлекает за собой нижний соседний слой с силой
. Важно отметить, что частицы жидкости, прилегающие к верхней пластине, движутся вместе с нею со скоростью v (увлекаются пластиной). Напротив, частицы жидкости вблизи нижней (неподвижной) пластины находятся в покое (прилипают к пластине). Если мысленно разбить жидкость на параллельные плоские слои, движущиеся равномерно, то нетрудно понять, что каждый вышележащий слой увлекает за собой нижний соседний слой с силой 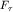 . В свою очередь, этот нижний слой тормозит движение верхнего слоя с силой, численно равной
. В свою очередь, этот нижний слой тормозит движение верхнего слоя с силой, численно равной 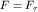 , приложенной к верхней пластине, передается на нижнюю пластину. Коэффициент вязкости среды определяется экспериментально, например, по скорости ее истечения через трубку известных размеров. (см. ниже). Как показывает опыт с нагреванием, вязкость жидкости уменьшается, а газов - увеличивается. Объяснение такого разного поведения коэффициента вязкости будет дано в курсе "Молекулярная физика".
, приложенной к верхней пластине, передается на нижнюю пластину. Коэффициент вязкости среды определяется экспериментально, например, по скорости ее истечения через трубку известных размеров. (см. ниже). Как показывает опыт с нагреванием, вязкость жидкости уменьшается, а газов - увеличивается. Объяснение такого разного поведения коэффициента вязкости будет дано в курсе "Молекулярная физика".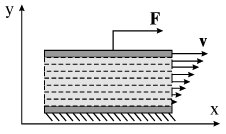

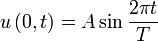 или
или 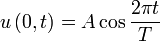
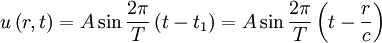 где c — скорость распространения волны в данной среде.
где c — скорость распространения волны в данной среде.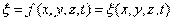
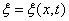 . Пусть колебание точек, лежащих в плоскости
. Пусть колебание точек, лежащих в плоскости 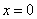 , имеет вид (при начальной фазе
, имеет вид (при начальной фазе 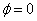 )
)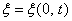
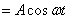
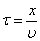 .
.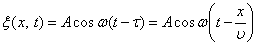 ,
,
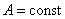 . Это будет, если энергия волны не поглощается средой.
. Это будет, если энергия волны не поглощается средой. , или
, или 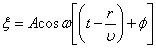 .
.
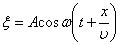 .
.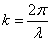 , или в векторной форме:
, или в векторной форме: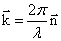 ,
,
 – волновой вектор,
– волновой вектор, 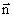 – нормаль к волновой поверхности.
– нормаль к волновой поверхности.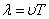 , то
, то 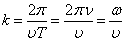 . Отсюда
. Отсюда 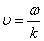 . Тогда уравнение плоской волны запишется так:
. Тогда уравнение плоской волны запишется так: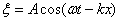 .
.
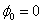 ). Тогда точки, лежащие на волновой поверхности радиуса r, будут иметь фазу
). Тогда точки, лежащие на волновой поверхности радиуса r, будут иметь фазу 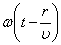 . Амплитуда колебаний здесь, даже если волна не поглощается средой, не будет постоянной, она убывает по закону
. Амплитуда колебаний здесь, даже если волна не поглощается средой, не будет постоянной, она убывает по закону 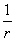 . Следовательно, уравнение сферической волны:
. Следовательно, уравнение сферической волны: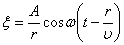 , или
, или 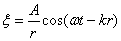 ,
,
 , амплитуда стремится к бесконечности. То, что амплитуда колебаний
, амплитуда стремится к бесконечности. То, что амплитуда колебаний 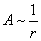 , следует из рассмотрения энергии, переносимой волной.
, следует из рассмотрения энергии, переносимой волной.