
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Частотное (статистическое) определениеСтр 1 из 3Следующая ⇒
Вопросы по теор. вер. и мат. стат. Вопрос 1. Испытание события. Испытание – это некий опыт с, созданными для наступления события, условиями. Событие – результат испытания. События: 1) достоверные. Всегда происходят 2)невозможные. Никогда не происходят 3)случайные. Могут произойти и не произойти при равных начальных условиях 0 < Случайное событие- событие является случайным, если при одинаковых условиях оно может произойти или не произойти. События: 1)совместные, 2)несовместные Несовместные, если появление одного события исключает появление других событий в одном и том же испытании. Появление хотя бы одного из нескольких событий в результате испытания образуют ПОЛНУЮ ГРУППУ. Равновозможные события. Противоположные события- 2 события, образующие полную группу. Независимые события. Событие В называют независимым от события А. если появление события А не изменяет вероятности события В, т.е. если условная вероятность события В равна его безусловной вероятности. Два события называются независимыми, если вероятность их совмещения равна произведению вероятностей этих событий; в противном случае - зависимые. Несколько событий называют попарно независимыми, если каждые два из них независимы.
Вопрос 2. Вероя́тность — степень (мера, количественная оценка) возможности наступления некоторого события. Когда основания для того, чтобы какое-нибудь возможное событие произошло в действительности, перевешивают противоположные основания, то это событие называют вероятным, в противном случае — невероятным или маловероятным. Классическая вероятность Наряду с понятием равновозможности в общем случае для классического определения необходимо также понятие элементарного события (исхода), благоприятствующего или нет изучаемому событию A. Речь идет об исходах, наступление которых исключает возможность наступления иных исходов. Это несовместимые элементарные события. К примеру при бросании игральной кости выпадение конкретного числа исключает выпадение остальных чисел. Классическое определение вероятности можно сформулировать следующим образом: Вероятностью случайного события A называется отношение числа n несовместимых равновероятных элементарных событий, составляющих событие A, к числу всех возможных элементарных событий N:
Например, пусть подбрасываются две кости. Общее количество равновозможных исходов (элементарных событий) равно очевидно 36 (6 возможностей на каждой кости). Оценим вероятность выпадения 7 очков. Получение 7 очков возможно следующими способами: 1+6, 2+5, 3+4, 4+3, 5+2, 6+1. То есть всего 6 равновозможных исходов, благоприятствующих событию A — получению 7 очков. Следовательно, вероятность будет равна 6/36=1/6. Для сравнения вероятность получения 12 очков или 2 очков равна всего 1/36 — в 6 раз меньше. Комбинаторные задачи на перестановки. Перестановками называют комбинации, состоящие из одних и тех же n различных элементов и отличающихся только порядком расположения. Формула Общая постановка задачи: Каким количеством способов можно разместить N объектов на М мест. Особая разновидность задач на перестановки-объекты расположенные по кругу.
2 стул
3 стул Комбинаторная задача на вычисление числа сочетаний. Сочетаниями называют комбинации, составленные из n различных элементов по m элементов. которые отличаются хотя бы одним элементом. Формула Общая постановка задачи. Каким количеством способов можно выбрать М объектов из N? Ч К Б: Задача. Сколькими способами можно выбрать 5 деталей из ящик, содержащего10 деталей?
Вопрос№ 7. Комбинаторика – раздел математики, в котором изучаются вопросы о том, сколько различных конфигураций (комбинаций), подчиненных тем или иным условиям, можно составить из заданных объектов. Большинство комбинаторных задач решается с помощью двух основных правил - правила суммы и правила произведения. Правило суммы. Если некоторый объект A можно выбрать n способами, а другой объект B можно выбрать m способами, то выбор "либо A, либо B" можно осуществить n+m способами. Правило произведения. Если объект A можно выбрать n способами, а после каждого такого выбора другой объект B можно выбрать (независимо от выбора объекта А) m способами, то пары объектов A и B можно выбрать n*m способами.
Вопрос №8. Случайной называют величину, которая в результате испытания примет одно и только одно возможное значение, наперед не известное и зависящее от случайных причин, которые заранее не могут быть учтены. Законом распределения дискретной случайной величины называют соответствие между возможными значениями и их вероятностями. Законом распределения дискретной случайной величины называется всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими вероятностями. Про случайную величину говорят, что она подчиняется данному закону распределения. Вопрос№9.
Бернулли: Дискретная случайная величина имеет биномиальный закон распределения (закон распределения Бернулли), если она принимает целочисленные неотрицательные значения 0, 1, 2, 3, …, m, …, n с вероятностями, вычисляемыми по формуле Бернулли: где q=1-p; Биномиальный закон распределения. Случайная величина X принимает значения: 0, 1, 2, 3, 4, 5,..., п, с вероятностью, определяемой по формуле Бернулли
Вопрос№10. Геометрический закон распределения. Испытания проводятся до наступления события. Событие происходят с постоянной вероятностью. P=(const) P(A)=q^n-1*p
Вопрос№11.
ГИПЕРГЕОМЕТРИЧЕСКОЕ РАСПРЕДЕЛЕНИЕ
Гипергеометрический закон определяется тремя параметрами N, М, п. При n<0, 1N этот закон стремится к биномиальному.
Вопрос№12. Распределение Пуассона — вероятностное распределение дискретного типа, моделирует случайную величину, представляющую собой число событий, произошедших за фиксированное время, при условии, что данные события происходят с некоторой фиксированной средней интенсивностью и независимо друг от друга. Теорема. Если вероятность р наступления события А в каждом испытании постоянно близка к нулю, число независимых испытаний n достаточно велико, произведение np = λ, то вероятность Рn(m) того, что в n независимых испытаниях события А наступит m раз, приближенно равна
Простейший поток событий Потоком событий называют последовательность событий, которые наступают в случайные потоки времени. Простейшим(Пуассоновским) называют поток событий, обладает тремя свойствами: 1)стационарность, 2) отсутствие последствия, 3) ординарность. Сво-во стационарности. Вероятность появления k событий в любом промежуткевремени зависит только от числа k и от длительности промежутка времени и не зависит от начала отсчета. Свойство отсутствие последствия. Вероятность появления k событий не зависти от того появились или нет события в промежуток времени, предшествующее началу рассмотрения промежутка. Свойство ординарности Появление двух и более событий за малый промежуткок времени практически невозможно. Интенсивность потока λ называют сореднее число событий, которое появляется в еденицу времени. Если извеестна λ, то вероятность появления k событий простейшего потока за t определяется функцией
15.
16. Мат. ожидание дискретной случайной величины и его сво-ва
Вопрос 18. Средним квадратическим отклонением случайной величины X называется квадратный корень из дисперсии: s (X) = D (X). Дисперсия имеет размерность, равную квадрату размерности случайной величины. Поэтому в тех случаях, когда желательно, чтобы оценка рассеяния имела размерность случайной величины, вычисляют среднее квадратическое отклонение, а не дисперсию. Например, если X выражается в метрах, то s (X) будет выражаться тоже в метрах, а D (X) - в квадратных метрах. Пример. Найти среднее квадратическое отклонение случайной величины X, которая задана следующим рядом распределения:
Решение: Математическое ожидание M(X) = 2∙0,1+3∙0,4+10∙0,5 = 6,4. Тогда M (X2) = 22∙0,1+32∙0,4+102∙0,5 = 54. Дисперсия D(X) = M(X2) – [M(X)]2=54 – (6,4 )2=13,04. Искомое среднее квадратическое отклонение s (X) = D (X) = 13,04» 3,61. Вопрос 19 Рассмотрим Вопрос 20. Непрерывные случайные величины. -Это возможные значения непрерывно заполняют собой некоторый промежуток. Задать ряд распределения не возможно т.к. F(x)=m/n=1/ ∞
Используют F(x)=P(X<x)-интегральную функцию распределения И f(x)=F(x)-функцию плотности распределения. Дифференциальную функцию распределения Вопросы по теор. вер. и мат. стат. Вопрос 1. Испытание события. Испытание – это некий опыт с, созданными для наступления события, условиями. Событие – результат испытания. События: 1) достоверные. Всегда происходят 2)невозможные. Никогда не происходят 3)случайные. Могут произойти и не произойти при равных начальных условиях 0 < Случайное событие- событие является случайным, если при одинаковых условиях оно может произойти или не произойти. События: 1)совместные, 2)несовместные Несовместные, если появление одного события исключает появление других событий в одном и том же испытании. Появление хотя бы одного из нескольких событий в результате испытания образуют ПОЛНУЮ ГРУППУ. Равновозможные события. Противоположные события- 2 события, образующие полную группу. Независимые события. Событие В называют независимым от события А. если появление события А не изменяет вероятности события В, т.е. если условная вероятность события В равна его безусловной вероятности. Два события называются независимыми, если вероятность их совмещения равна произведению вероятностей этих событий; в противном случае - зависимые. Несколько событий называют попарно независимыми, если каждые два из них независимы.
Вопрос 2. Вероя́тность — степень (мера, количественная оценка) возможности наступления некоторого события. Когда основания для того, чтобы какое-нибудь возможное событие произошло в действительности, перевешивают противоположные основания, то это событие называют вероятным, в противном случае — невероятным или маловероятным. Классическая вероятность Наряду с понятием равновозможности в общем случае для классического определения необходимо также понятие элементарного события (исхода), благоприятствующего или нет изучаемому событию A. Речь идет об исходах, наступление которых исключает возможность наступления иных исходов. Это несовместимые элементарные события. К примеру при бросании игральной кости выпадение конкретного числа исключает выпадение остальных чисел. Классическое определение вероятности можно сформулировать следующим образом: Вероятностью случайного события A называется отношение числа n несовместимых равновероятных элементарных событий, составляющих событие A, к числу всех возможных элементарных событий N:
Например, пусть подбрасываются две кости. Общее количество равновозможных исходов (элементарных событий) равно очевидно 36 (6 возможностей на каждой кости). Оценим вероятность выпадения 7 очков. Получение 7 очков возможно следующими способами: 1+6, 2+5, 3+4, 4+3, 5+2, 6+1. То есть всего 6 равновозможных исходов, благоприятствующих событию A — получению 7 очков. Следовательно, вероятность будет равна 6/36=1/6. Для сравнения вероятность получения 12 очков или 2 очков равна всего 1/36 — в 6 раз меньше.
Частотное (статистическое) определение Классическое определение при рассмотрении сложных проблем наталкивается на трудности непреодолимого характера. В частности, в некоторых случаях выявить равновозможные случаи может быть невозможно. Даже в случае с монеткой, как известно существует явно не равновероятная возможность выпадения «ребра», которую из теоретических соображений оценить невозможно (можно только сказать, что оно маловероятно и то это соображение скорее практическое). Поэтому еще на заре становления теории вероятностей было предложено альтернативное «частотное» определение вероятности. А именно, формально вероятность можно определить как предел частоты наблюдений события A, предполагая однородность наблюдений (то есть одинаковость всех условий наблюдения) и их независимость друг от друга:
где
2) Классическое определение вероятности предполагает, что число элементарных исходов испытания конечно. На практике же весьма часто встречаются испытания, число возможных исходов которых бесконечно. Действительно, если событие достоверно, то т = п и относительная частота m/n=n/n=1 т. е. статистическая вероятность достоверного события (так же как и в случае классического определения) равна единице. Если событие невозможно, то т — 0 и, следовательно, относительная частота 0/n=0 т. е. статистическая вероятность невозможного события равна нулю. Для любого события 0<=m>=n и, следовательно, относительная частота 0<=m/n<=1. т. е. статистическая вероятность любого события заключена между нулем и единицей. Для существования статистической вероятности события А требуется: а) возможность, хотя бы принципиально, производить неограниченное число испытаний, в каждом из которых событие А наступает или не наступает; б) устойчивость относительных частот появления А в различных сериях достаточно большого числа испытаний.
|
|||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 367; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.65.65 (0.089 с.) |
 .
. .
. < 1.
< 1. (В)= Р(В)
(В)= Р(В)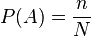
 =n!= n(n-1)(n-2)…
=n!= n(n-1)(n-2)…


 6 способов 1 стул 2 стул
6 способов 1 стул 2 стул
 2 стул 3 стул
2 стул 3 стул
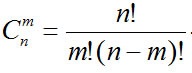 - число сочетаний из n элементов по m.
- число сочетаний из n элементов по m.


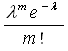 , т.е.
, т.е.
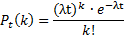





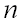 взаимно независимых случайных величин
взаимно независимых случайных величин  , которые имеют одинаковые распределения, а, следовательно, и одинаковые числовые характеристики (математическое ожидание, дисперсию, среднее квадратическое отклонение и другие).
, которые имеют одинаковые распределения, а, следовательно, и одинаковые числовые характеристики (математическое ожидание, дисперсию, среднее квадратическое отклонение и другие).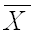 среднее арифметическое рассматриваемых случайных величин:
среднее арифметическое рассматриваемых случайных величин: .
.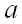 каждой из величин:
каждой из величин: .
.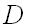 каждой из величин:
каждой из величин: .
. раз среднего квадратического отклонения
раз среднего квадратического отклонения  каждой из величин:
каждой из величин: .
.
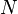 — количество наблюдений, а
— количество наблюдений, а 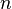 — количество наступлений события
— количество наступлений события  .
.


