
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Статистическая обработка результатов прямых многократных измерений во время вычислительной практики.
Одной из основных задач вычислительной практики является – научить студента не только правильно проводить измерения физических величин, но и точно получать количественную информацию о ней. Основной задачей любых измерений является извлечение с заданной точностью и достоверностью количественной информации о физических величинах. Поскольку измерения практически всегда сопровождаются появлением случайных погрешностей, то обработка результатов измерений должна включать в себя операций над случайными величинами. Эти операции выполняются с помощью теории вероятности и математической статистики. Статистическая обработка результатов измерений - обработка измерительной информации с целью получения достоверных данных. В настоящее время в отечественной метрологии наибольшее развитие получила теория измерений, основанная на понятии «погрешность» и являющаяся пока основой для большинства действующих в Российской Федерации нормативных документов. Дело в том, что при проведении практических измерений всегда важно оценить их точность. Понятие «точность измерений», т.е. степень приближения результатов измерения к истинному значению, обычно используют для качественного сравнения измерительных операций. Для количественной оценки применяют понятие «погрешность измерений». Поэтому для экспериментатора нахождение погрешности измерений – одно из важных действий по обеспечению единства измерений. Задача статистической обработки результатов многократных измерений заключается в нахождении измеряемой величины и доверительных границ, в которых находится её истинное значение. Статистическую обработку используют для повышения точности многократных измерений, а также определения статистических характеристик случайной погрешности. Вместе с тем из результатов измерений невозможно полностью исключить и систематические погрешности измерений. И поскольку всегда остаются неисключенные систематические погрешности (НСП), то для их уменьшения статистическая обработка результатов измерений также необходима. Для прямых однократных измерений статистическая обработка менее сложна и громоздка, что значительно упрощает оценку погрешностей. В производственных условиях точность таких измерений обычно оказывается вполне приемлемой. Вместе с тем практически всегда необходимо провести оценку их результатов.
Если в результатах измерений один или два существенно отличаются от остальных, а наличия ошибки в снятии показаний, описки и других ошибок не обнаружено, то необходимо проверить, не являются ли они промахами, подлежащими исключению. Необходимость в многократных измерениях некоторой физической величины xи=xд=A (обозначение A введено для удобства) возникает при наличии в процессе измерений значительных случайных погрешностей. При этом задача статистической обработки в том, чтобы по результатам измерений определить значение измеряемой величины, близкое к истинному xи=A, и границы, в которых оно находится с заданной вероятностью. Задачу решают статистической обработкой результатов измерений, основанной на гипотезе о распределении случайных погрешностей по нормальному закону. Такую обработку необходимо проводить в соответствии с государственным стандартом и рекомендациями по метрологии. Методика обработки результатов измерений дается применительно к прямым многократным и равноточным измерениям и дополнена пояснениями. Определение результата измерения и среднего квадратичного отклонения (средней квадратичной погрешности) СКО (СКП). Для удобства анализа предположим, что при выполнении п многократных прямых измерений одной и той же физической величины xи=A постоянная систематическая погрешность Δс полностью исключена (равна нулю). Тогда результат i-го измерения xi=xи+Ai получают с некоторой абсолютной случайной погрешностью Д, записанную в виде: Δi=Δio=xi+xи При нормальном законе распределения случайной погрешности Δi а истинную величину xи=A принимают её среднее арифметическое значение, равное математическому ожиданию m1 выполненного ряда из n измерений, т.е. полагают, что x=A=m1 есть результат измерения x= Зная результат измерения величины xи вычисляют абсолютную погрешность каждого из n измерения Центральный момент второго порядка, называемый дисперсией (англ. dispersion), характеризует расстояние погрешностей относительно центра распределения Δ=0
Чем больше дисперсия, тем значительнее рассеяние погрешностей относительно центра распределения (среднего значения; англ. average value; часто mean value). Дисперсия имеет размерность квадрата погрешности и поэтому неудобна как характеристика рассеяния. Обычно вместо дисперсии используют среднюю квадратичную погрешность (СКП; далее пока более применимое среднее квадратичное отклонение – СКО)
Которая имеет размерность самой погрешности. Далее, воспользовавшись формулами (1) и (2), находят СКО
Результат измеряемого значения xи зависит от числа измерений n и безусловно является случайной величиной. Поэтому удобно вычислять СКО величины Данное СКО характеризует степень разброса измеренных значений
Формулы (3) и (4) соответствуют центральной предельной теории вероятностей и показывают, что точность метода (это относится к одному измерению) и точность результата многократных измерений увеличиваются с ростом числа n. Среднее арифметическое значение ряда n измерений всегда имеет меньшую погрешность, чем погрешность одного определенного измерения. Это отражает формула (4), определяющая фундаментальный закон теории погрешностей, из которого следует что для повышения точности результата (при исключенной систематической погрешности), например, в 2 раза, необходимо число измерений увеличить в 4 раза; если требуется повысить точность измерений в 5 раз, то их число увеличивают в 25 раз и т.д. Следует четко разграничивать применение СКО Рассмотрим случай многократных измерений, когда результат конкретного i-го измерения содержит и случайную
Подстановка значений xi в формулу (1) позволяет получить результат измерений x в следующем виде:
Из этого выражения следует, что многократные измерение и увеличение их числа n не влияют на систематическую составляющую погрешности результата измерений, но уменьшают случайную (за счет разных знаков отдельных погрешностей Актуальность данного вопроса – первопланова, т.к. неопытному оператору (студенту первокурснику) трудно получить (без промахов) точную количественную информацию. Поэтому одной из основных задач вычислительной практики является – научить студента не только правильно проводить измерения физических величин, но и точно получать количественную информацию о ней. Обнаружение и исключение промахов из результата измерений. При однократном измерении величины промах может быть обнаружен только путем логического анализа или сопоставления результата с априорной информацией о нем. Если причина промаха установлена, то результат однократного измерения следует признать ошибочным и повторить измерение. При многократных измерениях одной и той же величины постоянного размер промахи проявляются в том, что результаты отдельных измерений, входящих в один ряд, резко отличаются от остальных результатов этого ряда.
Решение задачи исключения промахов выполняют общими методами проверки статистических гипотез. Проверяемая гипотеза состоит в утверждении, что результат i-го измерения xi не содержит промаха, т.е. является одним из значений измеряемой величины. Пользуясь определенными статистическими критериями, пытаются опровергнуть выдвинутую гипотезу. Если это удается, то этот результат измерения рассматривают как промах и его исключают. Общие методы исключения промахов. Вопрос об исключении промахов невозможно однозначно решить в общем виде, поскольку для принятия такого решения требуется тщательный анализ конкретных целей измерений, особенностей средств измерений и характера поведения измеряемой величины. Особую осторожность следует проявлять тогда, когда исследуются процессы с малоизученными характеристиками. Разработка и анализ методов исключения имеют большое практическое значение, поскольку при использовании сложной измерительной аппаратуры доля аномальных результатов может достигать 10..15% общего числа измерений. Рассмотрим методики использования некоторых критериев. Критерий «трех сигм». Данный критерий применяют для результатов измерений, распределённых по нормальному закону, и одним из граничных параметров служит оценка СКО измерений Критерий оценки аномальности (иногда – анормальности) результатов измерений при неизвестном СКП (СКО) 1.Результаты группы из n многократных измерений, называемые выборкой, упорядочивают по возрастанию xj<x2<…< xn. По формулам (1) и (3) вычисляют среднее арифметическое значение
2. Задаются уровнем значимости критерия ошибки q. Очевидно, этот уровень должен быть достаточно малым, чтобы вероятность ошибки была невелика. Из таблицы 5.1 по заданным параметрам q и n находят предельное (граничное) значение коэффициента
3. Сравнивают коэффициенты, определяемые по формулам (7) и (8) выполняются условия β1> βг и βn> βг, то результаты x1 и xn относят к промахам и исключают из полученных результатов измерений физической величины.
Таблица 3 Предельное значение коэффициента βг
Как видно из данных табл. 3, с уменьшением уровня значимости q коэффициент βг увеличивается при выбранном числе измерений п. Это означает, что при снижении значения q все меньше число результатов измерений может быть отнесено к промахам поскольку усложняется выполнение условия βi> βг. Поэтому слишком малые значения не используют, и они в табл.3 не показаны. Пример 5.1. При измерении сопротивления резистора получена упорядоченная выборка пяти следующих значений: 180; 182; 183; 184; 196 Ом. Требуется оценить результат измерения 196 Ом при заданном уровне значимости ошибки q=0,05. Решение. Для данной выборки по формулам (1) и (4) вычислим оценки среднего арифметического значения Пример 5.2. Проверить результаты 18 измерений сопротивления резистора R(Ом) представленные в табл.4, на наличие грубых погрешностей (промахов). Таблица 4 Результаты измерений
Решение. Упорядочим результаты измерений Ri по возрастанию (см. табл.5) и введем их нумерацию. Таблица 5 Упорядоченные результаты измерений
Проверим, не относится ли минимальное R1=8,283 Ом и максимальное R18=8,669 Ом значения измерений к грубым погрешностям. Порядок проверки следующий. 1. С помощью формул (1) - (4) последовательно вычислим результат измерений
Таблица 6. Расчетные значения к примеру 5.2
2. Приведем Расчет коэффициентов β1 и β18 по формуле (7)
3. Задаем уровнем значимости ошибки q=0,1. По числу приведённых измерений n=18 и значению q=0,1 из табл.3 найдем значение коэффициента βг=2,34. 4. Убедимся, что результаты измерений R1 и R18 не являются грубыми погрешностями, так как β1 < βг и β18 < βг и сделаем аналогичный вывод для всех результатов измерений. При небольшом числе измерений (до 10) рекомендовано использовать критерий Шовине. Согласно этому критерию, промахом считают результат xi, если абсолютная разность 1,6σ при n=3
1,9σ при n=8 2,0σ при n=10 Пример 5.3. При 10 измерениях напряжения получены следующие результаты: 12,10; 12,12; 12,07; 12;40; 12,08; 12,13; 12,15; 12,16; 12,20; 12,17 В. Следует проверить, не является ли промахом значения напряжения 12,4 В? Решение: Обработав полученные результаты измерений, получим такие значения:
Согласно критерию Шовине (9) Пример 5.3а. При измерении восьми значений емкости конденсатора получены следующие результаты: 1338, 1315, 1344, 1361, 1321, 1384, 1367 и 350 используя критерий Шовине, не является ли пятый результат промахом? Решение: находим среднее арифметическое по формуле
Тогда
Тогда согласно критерию Шовине (9):
Следовательно, данное измерение (1384) не является промахом.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 250; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.188.160 (0.038 с.) |
 (1)
(1)


 (2)
(2)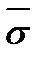 величины
величины  , характеризующую точность метода измерений.
, характеризующую точность метода измерений. (3)
(3) , которую назовём СКО результата измерения, записав
, которую назовём СКО результата измерения, записав  , или проще
, или проще  .
. (4)
(4) и
и  величину
величину  используют при оценке погрешностей окончательного результата многократных измерений, а
используют при оценке погрешностей окончательного результата многократных измерений, а 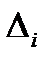 , и постоянную систематическую
, и постоянную систематическую  составляющие погрешности, т.е.
составляющие погрешности, т.е.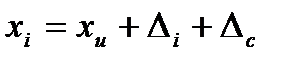 (5)
(5) (6)
(6)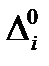 - очевидно, что они могут быть как со знаком «+», так и со знаком «-»). Поэтому в случае, когда в результате многократных измерений преобладает систематическая погрешность (например, при использовании прибора малой точности), следует ограничиться одним-двумя измерениями. Вопрос ограничения числа многократных измерений рассмотрен ниже.
- очевидно, что они могут быть как со знаком «+», так и со знаком «-»). Поэтому в случае, когда в результате многократных измерений преобладает систематическая погрешность (например, при использовании прибора малой точности), следует ограничиться одним-двумя измерениями. Вопрос ограничения числа многократных измерений рассмотрен ниже. . По этому критерию считается, что результат, полученный с уровнем значимости q < 0.003 (соответственно вероятностью P > 0.997), маловероятен и его можно считать промахом, если
. По этому критерию считается, что результат, полученный с уровнем значимости q < 0.003 (соответственно вероятностью P > 0.997), маловероятен и его можно считать промахом, если 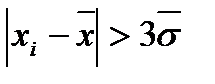 . Значения q и
. Значения q и 
 и СКО
и СКО 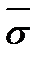 этой выборки. Для предполагаемых промахов, которыми могут быть, например, показания x1 и xn проводят расчет коэффициентов
этой выборки. Для предполагаемых промахов, которыми могут быть, например, показания x1 и xn проводят расчет коэффициентов
 (7)
(7) (8)
(8) Ом и СКО измерений
Ом и СКО измерений  , абсолютную погрешность
, абсолютную погрешность  каждого измерения (расчетные значения представлены таблице 6) и СКО проверенных измерений
каждого измерения (расчетные значения представлены таблице 6) и СКО проверенных измерений  Ом
Ом 




 превышает значения СКО σ с некоторым коэффициентом, зависящим от числа многократных измерений n:
превышает значения СКО σ с некоторым коэффициентом, зависящим от числа многократных измерений n: > 1,7σ при n=6 (9)
> 1,7σ при n=6 (9)

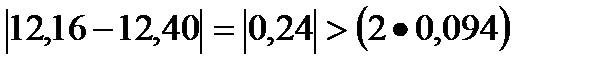 . Значит четвёртый результат измерения 12,40 В является промахом.
. Значит четвёртый результат измерения 12,40 В является промахом.
 =1347,5. Определяем разность между каждым измеренным результатом и средним значением. Тогда имеем: (-9,5)2=90,25; (-32,5)2=1056,25;..2,52=6,25; посчитаем по формуле:
=1347,5. Определяем разность между каждым измеренным результатом и средним значением. Тогда имеем: (-9,5)2=90,25; (-32,5)2=1056,25;..2,52=6,25; посчитаем по формуле: пФ
пФ



