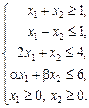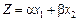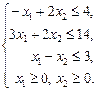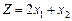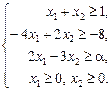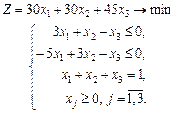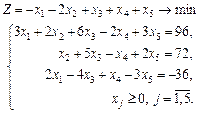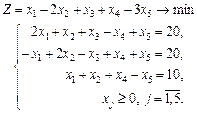Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Загальні задачі лінійного програмування та методи їх розв’язуванняСтр 1 из 7Следующая ⇒
1.1. Приклади розв’язування задач ЛП графічним методом Приклад 1.1 Фірма виготовляє два продукти А та В, що продаються відповідно по 8 та 15 центів за упаковку. Ринок збуту для кожного з них практично необмежений. Продукт А обробляється верстатом 1, а продукт В — верстатом 2. Далі обидва продукти упаковуються на фабриці. Ціна 1 кг сировини — 6 центів. Верстат 1 обробляє за годину 5000 кг сировини, а верстат 2 — 4000 кг сировини із втратами, що становлять відповідно 10 і 20 %. Верстат 1 може працювати 6 год на день, причому його використання коштує 288 дол./год; верстат 2 — 5 год на день, що коштує 336 дол./год. Маса однієї упаковки продукту А дорівнює 1/4 кг, а продукту В 1/3 кг. Фабрика може працювати 10 год на день, виготовляючи за 1 год продукції на 360 дол. упаковуючи 12 000 продуктів А та 8000 продуктів В. Відшукати такі значення х 1 та х 2 споживання сировини для продуктів А та В (у тисячах кілограмів), які забезпечують найбільший щоденний прибуток фірми. Сформулюємо математично задачу й розв’яжемо її графічно.
Побудова математичної моделі. Нехай х 1 —кількість сировини, тис. кг, використовуваної для виготовлення продукту А, а х 2 — кількість сировини, тис. кг, що йде на виготовлення продукту В. Запишемо обмеження задачі. Згідно з умовою обмеженими ресурсами є час використання верстатів 1 і 2, а також час роботи фабрики з упакування продуктів А та В. 1. Обмеження на використання верстата 1. Економічний зміст цього обмеження такий: фактичний час роботи верстата 1 з обробки сировини для продукту А не повинен перевищувати 6 год, тобто
Математично це запишеться так: х 1 / 5 ≤ 6, або х 1 ≤ 30. 2. Обмеження на використання верстата 2 знаходимо аналогічно: х 2 / 4 ≤ 5, або х 2 ≤ 20. 3. Обмеження на час роботи фабрики з упакування продуктів А та В. Економічний зміст цього обмеження такий: фактичний час, витрачений на упакування продуктів А та В, не повинен перевищувати 10 год на день:
Математично це запишеться так:
або 0,3 х 1 + 0,3 х 2 ≤ 10, 3 х 1 + 3 х 2 ≤ 100. Побудуємо цільову функцію задачі. Прибуток фірми складається з різниці між доходом від реалізації виготовленої продукції та витратами на її виробництво. 1. Дохід, дол., від виробництва продуктів А та В визначається так:
або
Загальний дохід дорівнює 288 х 1 + 360 х 2. 2. Витрати, дол., на сировину визначаємо як загальну кількість сировини, тис. кг, використовуваної для виробництва продуктів А та В, помножену на вартість одиниці сировини, дол.: 60 (х 1 + х 2) = 60 х 1 + 60 х 2. 3. Витрати, дол., пов’язані з використанням верстатів 1 і 2, визначаємо як фактичний час роботи верстата з обробки сировини, помножений на вартість 1 год роботи відповідного верстата:
4. Витрати, дол., пов’язані з упакуванням продуктів А та В, складаються з фактичного часу роботи фабрики (0,3 х 1 + 0,3 х 2), помноженого на вартісний еквівалент 1 год роботи фабрики, який становить 360 дол.: 360 (0,3 х 1 + 0,3 х 2) = 108 х 1 + 108 х 2. Узагальнюючи всі складові частини цільової функції, можемо записати математичний вираз прибутку фірми за день: Z = (288 х 1 + 360 х 2) – (60 х 1 + 60 х 2) – (288/5 х 1 + 84 х 2) – (108 х 1 + 108 х 2) = Отже, маємо остаточний запис економіко-математичної моделі: Z = 12/5 · (26 х 1 + 45 х 2) ® max за обмежень
Незважаючи на порівняно складний процес моделювання, математично поставлена задача дуже проста й легко розв’язується графічно. Розв’язування. Графічне розв’язування задачі ілюструє рис. 1.1. Областю допустимих планів, що утворюється системою обмежень задачі, є многокутник О АВСD. Найбільшого значення цільова функція досягає у вершині В. Координати цієї точки визначаються із системи рівнянь:
Оптимальний план задачі Х * = (40/3; 20); max Z = 2992. Отже, для того, щоб отримати найбільший денний прибуток 2992 дол., фірма має обробляти 40/3 тис. кг сировини, виробляючи продукт А, і 20 тис. кг — виробляючи продукт В. За такого оптимального плану випуску продукції верстат 2 працюватиме 20/4 = 5 год на день, тобто з повним навантаженням, а верстат 1 працюватиме лише 40/15 = 2 год 20 хв на день.
Рис. 1.1. Приклад 1.2 На меблевій фабриці зі стандартних листів фанери потрібно вирізати 24, 28 і 18 заготовок трьох розмірів. Лист фанери можна розрізати двома способами. Кількість отриманих заготовок та площу відходів за кожного способу розрізування одного листа фанери наведено в таблиці:
Скільки листів фанери та за яким способом слід розрізати, щоб отримати потрібну кількість заготовок з мінімальними відходами.
Побудова математичної моделі. Нехай х 1, х 2 — кількість листів фанери, які необхідно розрізати відповідно першим і другим способом. Цільова функція — мінімізація відходів під час розрізування листа фанери. Математично це записується так: Z = 12 х 1 + 18 х 2 ® max. Обмеження математичної моделі враховують кількість заготовок кожного виду, які потрібно отримати: для заготовки 1 2 х 1 + 6 х 2 ≥ 24; для заготовки 2 4 х 1 + 4 х 2 ≥ 28; для заготовки 3 2 х 1 + 3 х 2 ≥ 18; Отже, економіко-математична модель задачі має вигляд Z = 12 х 1 + 18 х 2 ® min за обмежень
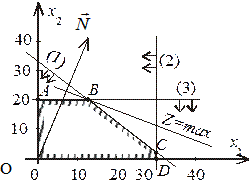
Розв’язування. Графічне розв’язування задачі оптимального розрізування ілюструє рис. 1.2. Область допустимих розв’язків цієї задачі необмежена. Вектор
Із рис. 1.2 бачимо, що пряма 12 х 1 + 18 х 2 = min Z збігається зі стороною ВС многокутника розв’язків. Це означає, що задача має альтернативні оптимальні плани: координати будь-якої точки відрізка BC є оптимальним планом, причому для цих координат цільова функція Z досягає свого найменшого значення. Визначимо лише два оптимальних плани, що відповідають кінцям відрізка BC. Точку В визначаємо із системи рівнянь
звідки Точку С визначаємо із системи рівнянь
отже, Повертаючись до економічного змісту розв’язаної задачі, маємо такі результати. Якщо розрізати 7 листів фанери, з яких 3 листи — першим способом, а 4 — другим, то матимемо найменшу площу відходів — 108 см2. Але такі самі мінімальні втрати будуть і в разі розрізування шести листів першим способом і двох — другим. Будь-який інший альтернативний оптимальний план задачі можна записати як опуклу лінійну комбінацію отриманих двох крайніх розв’язків:
де Наприклад, нехай l1 = l2 = 0,5. Тоді ще один оптимальний план задачі визначається так: Х * = 0,5 (3; 4) + 0,5 (6; 2). Х * = (4,5; 3). Цільова функція Z має таке саме мінімальне значення:
1.2 Приклади та завдання для самостійної роботи 1.1 Комерційна фірма рекламує свою продукцію, використовуючи місцеві радіо- та телевізійну мережі. Витрати на рекламу в бюджеті фірми становлять 10 000 дол. на місяць. Хвилина радіореклами коштує фірмі 5 дол., а телереклами — 90 дол. Фірма має намір використовувати радіорекламу принаймні вдвічі частіше, ніж рекламу на телебаченні. Досвід показав: обсяг збуту, що його забезпечує 1 хв телереклами, у 30 разів перевищує обсяг збуту, що його забезпечує 1 хв радіореклами. Визначити оптимальний розподіл коштів, які щомісяця мають витрачатися на рекламу, за якого обсягу збут продукції фірми буде найбільшим. 1.2 Невелике сільськогосподарське підприємство спеціалізується на вирощуванні овочів, зокрема капусти та томатів, використовуючи для цього мінеральні добрива (фосфорні та калійні). Норми внесення мінеральних добрив під кожну культуру та запас добрив у господарстві наведено в таблиці:
Під вирощування овочів відведено земельну ділянку площею 20 га. Очікуваний прибуток господарства від реалізації 1 ц капусти становить 10 ум. од., а 1 ц томатів — 20 ум. од. Середня врожайність капусти в господарстві дорівнює 300 ц/га, а томатів — 200 ц/га.
Визначити такий варіант розміщення культур на земельній ділянці, який максимізує прибуток господарства за умови, що витрати мінеральних добрив не перевищують максимально можливого запасу. 1.3 Фірма виготовляє два види продукції А та В, використовуючи для цього два види сировини, добовий запас якої має не перевищувати відповідно 210 та 240 ум. од. Витрати сировини для виготовлення одиниці продукції кожного виду подано таблицею:
Відділ збуту фірми вважає, що виробництво продукції В має становити не більш як 65 % загального обсягу реалізації продукції обох видів. Ціна одиниці продукції А та В дорівнює відповідно 10 та 40 дол. Визначити оптимальний план виробництва продукції, який максимізує дохід фірми. Записати економіко-математичну модель задачі та розв’язати її графічно. 1.4 Фірма виготовляє деталі до автомобілів, ринок збуту яких практично необмежений. Будь-яка деталь має пройти послідовну обробку на трьох верстатах, час використання кожного з яких становить 10 год/добу. Тривалість обробки, хв, однієї деталі на кожному верстаті наведено в таблиці:
Прибуток від оптової реалізації однієї деталі кожного виду становить відповідно 20 та 30 дол. Визначити оптимальні добові обсяги виробництва деталей кожного виду, що максимізують її прибуток. Записати економіко-математичну модель задачі та розв’язати її графічно. 1.5 Підприємство виготовляє письмові столи типів А та В. Для одного столу типу А необхідно 2 м2 деревини, а для столу типу В — 3 м2. Підприємство може отримати до 1200 м2 деревини за тиждень. Для виготовлення одного столу типу А потрібно 12 хв роботи обладнання, а для моделі В — 30 хв. Обладнання може використовуватися 160 год на тиждень. Оцінено, що за тиждень може бути реалізовано до 550 столів. Відомо, що прибуток від реалізації одного письмового столу типу А становить 30 дол., а типу В — 40 дол. Скільки столів кожного типу необхідно виготовляти за тиждень? Записати економіко-математичну модель задачі та розв’язати її графічно.
1.6 Підприємство електронної промисловості виготовляє дві моделі радіоприймачів, причому кожна модель складається на окремій технологічній лінії. Добовий обсяг виробництва першої лінії становить 60, а другої — 70 од. На один радіоприймач першої моделі витрачається 10 однотипних елементів електронних схем, а на радіоприймач другої моделі — 8. Максимальний добовий запас елементів, що використовуються у виробництві, становить 1000 од. Прибуток від реалізації одного радіоприймача першої та другої моделі дорівнює відповідно 35 та 25 дол. Визначити оптимальні обсяги виробництва радіоприймачів обох моделей. Записати економіко-математичну модель задачі та розв’язати її графічно. Графічним методом визначити оптимальні плани наступних задач лінійного програмування
1.27 Визначити екстремальні значення лінійної функції
у таких випадках: а) a = b = 2; б) a = – 9; b = 3; в) a = 6; b = 0.
1.28 Визначити максимум лінійної функції
за обмежень
у таких випадках: а) a = 3; b = 2; б) a = 1; b = 4; в) a = 5; b = 1.
1.29 Визначити найбільше значення функції
за обмежень
у таких випадках: а) a = –6; б) a = 4; в) a = 6. 1.30 Графічним методом визначити оптимальний план задачі лінійного програмування:
1.31 Розв’язати графічно таку задачу лінійного програмування:
1.32 Графічним методом розв’язати задачу лінійного програмування:
1.33 Розв’язати графічно задачу лінійного програмування:
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 1941; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.190.152.38 (0.05 с.) |
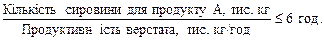
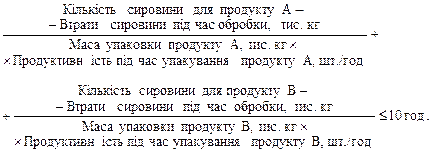
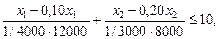
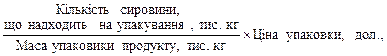
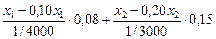 .
.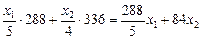 .
.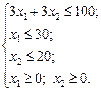
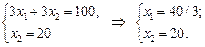
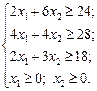
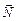 = (12; 18) можна змінити згідно з масштабом графіка, наприклад
= (12; 18) можна змінити згідно з масштабом графіка, наприклад 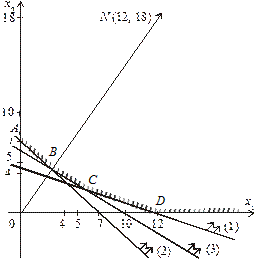 Рис. 1.2
Рис. 1.2
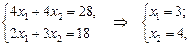
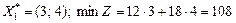 .
.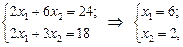
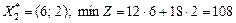 .
.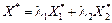 ,
, .
.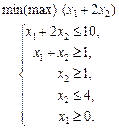
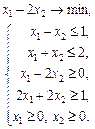
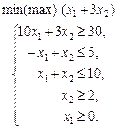
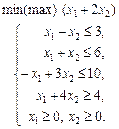
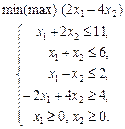
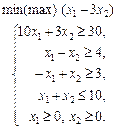
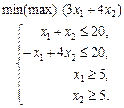
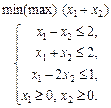
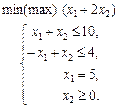
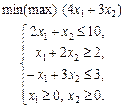
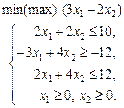
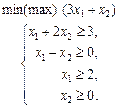
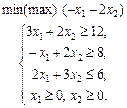
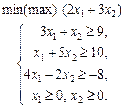
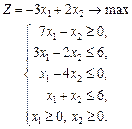
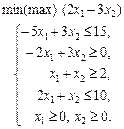
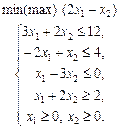
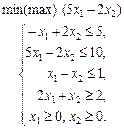
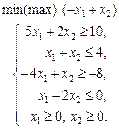
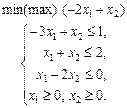
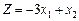 за обмежень
за обмежень